المعادلات التي تتضمن متغيرات في طرفيها
مقدمة
في رحلتنا عبر عالم الجبر، ننتقل من المعادلات البسيطة ذات الخطوة أو الخطوتين إلى معادلات أكثر تعقيدًا تتضمن المتغير نفسه في كلا طرفي علامة المساواة. يمثل هذا النوع من المعادلات تحديًا جديدًا ولكنه ضروري لتوسيع فهمنا للمساواة الجبرية وتطوير مهارات حل المشكلات الأكثر تقدمًا. تتطلب المعادلات التي تتضمن متغيرات في طرفيها استراتيجية إضافية لنقل الحدود وتجميع المتغيرات في طرف واحد والثوابت في الطرف الآخر قبل تطبيق العمليات العكسية لعزل المتغير وإيجاد قيمته. إن فهم مفهوم هذا النوع من المعادلات ومكوناتها، واستيعاب استراتيجية نقل الحدود وتجميع المتغيرات، وإدراك أهميتها في بناء أساس قوي للجبر وحل المشكلات الأكثر تعقيدًا في الرياضيات والعلوم، يمثل خطوة حاسمة في رحلة التعلم الجبري.
لقد نشأت الحاجة إلى حل المعادلات التي تتضمن متغيرات في طرفيها مع تطور المسائل الجبرية التي تصف علاقات أكثر تعقيدًا بين الكميات المتغيرة. ففي العديد من السيناريوهات الرياضية والعلمية، يظهر المتغير المجهول في كلا جانبي المعادلة، مما يستلزم اتباع خطوات منهجية لعزله. إن القدرة على حل هذه المعادلات بكفاءة ودقة تمكننا من تحليل هذه العلاقات المعقدة وإيجاد القيم التي تحقق التوازن بين الطرفين. علاوة على ذلك، يمثل هذا النوع من المعادلات خطوة هامة نحو فهم المعادلات الأكثر تجريدًا وتطبيقها في مجالات متنوعة مثل الفيزياء والهندسة والاقتصاد وعلوم الحاسوب.
مفهوم المعادلات التي تتضمن متغيرات في طرفيها ومكوناتها الأساسية
مفهوم المعادلة التي تتضمن متغيرات في طرفيها: هي معادلة جبرية تحتوي على متغير واحد (نفس المتغير) يظهر في كلا جانبي علامة المساواة. الهدف من حل هذا النوع من المعادلات هو تجميع جميع حدود المتغير في طرف واحد وجميع الثوابت في الطرف الآخر لعزل المتغير وإيجاد قيمته.
مكونات هذا النوع من المعادلات: بالإضافة إلى المكونات الأساسية للمعادلة الجبرية (المتغير، الثوابت، المعاملات، العمليات الحسابية)، تتميز هذه المعادلات بوجود حدود تحتوي على نفس المتغير في كلا الطرفين.
أمثلة على المعادلات التي تتضمن متغيرات في طرفيها:
- 3x+5=x−1
- 2y−7=5y+2
- 4a+3=−2a+9
- 21b−4=43b+1
استراتيجيات حل المعادلات التي تتضمن متغيرات في طرفيها بنقل الحدود
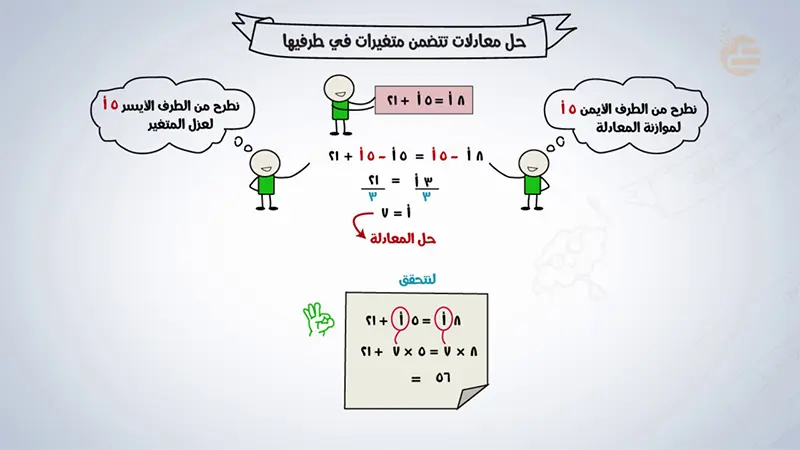
تعتمد الاستراتيجية الأساسية لحل هذا النوع من المعادلات على عملية نقل الحدود (Transposing Terms) لتجميع المتغيرات في طرف واحد والثوابت في الطرف الآخر. يتم نقل الحدود باستخدام العمليات العكسية (الجمع والطرح) للحفاظ على توازن المعادلة.
خطوات حل معادلة تتضمن متغيرات في طرفيها:
- تحديد حدود المتغيرات والثوابت: حدد الحدود التي تحتوي على المتغير والحدود الثابتة في كلا طرفي المعادلة.
- نقل حدود المتغيرات إلى طرف واحد: استخدم عملية الجمع أو الطرح لنقل جميع الحدود التي تحتوي على المتغير إلى أحد طرفي المعادلة (عادةً الطرف الذي يحتوي على معامل أكبر للمتغير لتجنب التعامل مع معاملات سالبة إذا أمكن). يجب تطبيق العملية نفسها على طرفي المعادلة.
- نقل الحدود الثابتة إلى الطرف الآخر: استخدم عملية الجمع أو الطرح لنقل جميع الحدود الثابتة إلى الطرف الآخر من المعادلة (الطرف الذي لا يحتوي على المتغير بعد الخطوة السابقة). يجب تطبيق العملية نفسها على طرفي المعادلة.
- تجميع الحدود المتشابهة: قم بتبسيط كلا طرفي المعادلة عن طريق تجميع الحدود المتشابهة (جمع أو طرح معاملات المتغيرات وجمع أو طرح الثوابت).
- عزل المتغير: بعد تجميع الحدود، ستحصل على معادلة ذات خطوة واحدة (مثل ax=b). استخدم عملية الضرب أو القسمة لعزل المتغير وإيجاد قيمته.
- التحقق من الحل: قم بتعويض قيمة المتغير التي تم الحصول عليها في المعادلة الأصلية للتأكد من أن طرفي المعادلة متساويان.
أمثلة توضيحية لحل المعادلات التي تتضمن متغيرات في طرفيها:
حل المعادلة 3x+5=x−1:
- حدود المتغيرات: 3x في الطرف الأيسر و x في الطرف الأيمن. الثوابت: 5 في الطرف الأيسر و −1 في الطرف الأيمن.
- نقل حدود المتغيرات إلى الطرف الأيسر (بطرح x من الطرفين): 3x−x+5=x−x−1⟹2x+5=−1.
- نقل الحدود الثابتة إلى الطرف الأيمن (بطرح 5 من الطرفين): 2x+5−5=−1−5⟹2x=−6.
- تجميع الحدود المتشابهة: تم التجميع بالفعل.
- عزل المتغير (بقسمة الطرفين على 2): 22x=2−6⟹x=−3.
- التحقق: 3(−3)+5=−9+5=−4 و (−3)−1=−4 (الحل صحيح).
حل المعادلة 2y−7=5y+2:
- حدود المتغيرات: 2y في الطرف الأيسر و 5y في الطرف الأيمن. الثوابت: −7 في الطرف الأيسر و 2 في الطرف الأيمن.
- نقل حدود المتغيرات إلى الطرف الأيمن (بطرح 2y من الطرفين): 2y−2y−7=5y−2y+2⟹−7=3y+2.
- نقل الحدود الثابتة إلى الطرف الأيسر (بطرح 2 من الطرفين): −7−2=3y+2−2⟹−9=3y.
- تجميع الحدود المتشابهة: تم التجميع بالفعل.
- عزل المتغير (بقسمة الطرفين على 3): 3−9=33y⟹y=−3.
- التحقق: 2(−3)−7=−6−7=−13 و 5(−3)+2=−15+2=−13 (الحل صحيح).
أهمية المعادلات التي تتضمن متغيرات في طرفيها وتطبيقاتها المتنوعة
يمثل فهم وحل المعادلات التي تتضمن متغيرات في طرفيها خطوة حاسمة في تطوير مهارات حل المشكلات الجبرية وتوسيع الفهم الرياضي:
- توسيع الفهم الجبري: يعزز هذا النوع من المعادلات فهم الطلاب لكيفية التعامل مع المساواة الجبرية ونقل الحدود للحفاظ على التوازن.
- تطوير مهارات حل المشكلات الأكثر تعقيدًا: يمثل هذا النوع من المعادلات مستوى أعلى من التحدي مقارنة بالمعادلات ذات الخطوة أو الخطوتين، مما يساعد في تطوير قدرة الطلاب على التفكير بشكل منهجي ومنطقي لحل المشكلات الأكثر تعقيدًا.
- ربط المفاهيم الرياضية بالمسائل الكلامية الأكثر تقدمًا: يمكن ترجمة العديد من المسائل الكلامية التي تصف علاقات أكثر تعقيدًا إلى معادلات تتضمن متغيرات في طرفيها.
- التأسيس لمفاهيم جبرية متقدمة: فهم كيفية حل هذه المعادلات ضروري للتعامل مع المتباينات التي تتضمن متغيرات في طرفيها، وأنظمة المعادلات الخطية، والدوال الخطية وتحليلها.
- التطبيقات في العلوم والهندسة: تظهر المعادلات التي تتضمن متغيرات في طرفيها في العديد من القوانين والنماذج العلمية والهندسية التي تصف علاقات بين كميات متغيرة تعتمد على بعضها البعض. على سبيل المثال، في تحليل الدوائر الكهربائية أو في وصف حركة الأجسام بتسارع ثابت.
أمثلة على مسائل كلامية يمكن حلها باستخدام معادلات تتضمن متغيرات في طرفيها:
- “لدى أحمد مبلغ من المال يزيد بمقدار 10 دولارات عما لدى سارة. إذا كان مجموع ما لديهما يساوي 50 دولارًا، فكم يملك كل منهما؟” (المعادلة: x+(x+10)=50)
- “قطاران يتحركان في اتجاهين متعاكسين. يسير القطار الأول بسرعة 60 كم/ساعة ويسير القطار الثاني بسرعة 80 كم/ساعة. بعد كم من الوقت سيصبح البعد بينهما 280 كم إذا كانا في البداية متجاورين؟” (المعادلة: 60t+80t=280)
الخاتمة
تُمثل المعادلات التي تتضمن متغيرات في طرفيها خطوة هامة في رحلة تعلم الجبر، حيث تتطلب تطبيق استراتيجيات أكثر تقدمًا لنقل الحدود وتجميع المتغيرات والثوابت. إن إتقان حل هذا النوع من المعادلات يعزز الفهم الجبري ويطور مهارات حل المشكلات الأكثر تعقيدًا، مما يفتح الباب أمام استكشاف مفاهيم جبرية أعمق وتطبيق الرياضيات في سياقات علمية وهندسية متنوعة. تظل القدرة على موازنة طرفي المعادلة بدقة هي المفتاح لإيجاد الحل الصحيح وفهم العلاقات الرياضية المعقدة.


