الدوال

مقدمة

في قلب الرياضيات يكمن مفهوم الدالة، الذي يمثل أداة قوية ومرنة لوصف العلاقات بين الكميات المتغيرة. يمكن تصور الدالة على أنها “آلة” رياضية تأخذ قيمة مدخلة (من مجموعة تسمى المجال) وتنتج قيمة مخرجة واحدة ومحددة (من مجموعة تسمى المدى) وفقًا لقاعدة أو قانون معين. إن فهم مفهوم الدالة ومكوناتها الأساسية (المجال، المدى، القاعدة)، واستيعاب أنواع الدوال المختلفة وخصائصها، وإدراك طرق تمثيلها (جبريًا، بيانيًا، جدوليًا)، يمثل أساسًا ضروريًا لاستكشاف عالم الرياضيات المتقدم وتطبيقاته الواسعة في نمذجة وتحليل الظواهر الطبيعية والاجتماعية والهندسية والاقتصادية وغيرها.

مفهوم الدالة ومكوناتها الأساسية

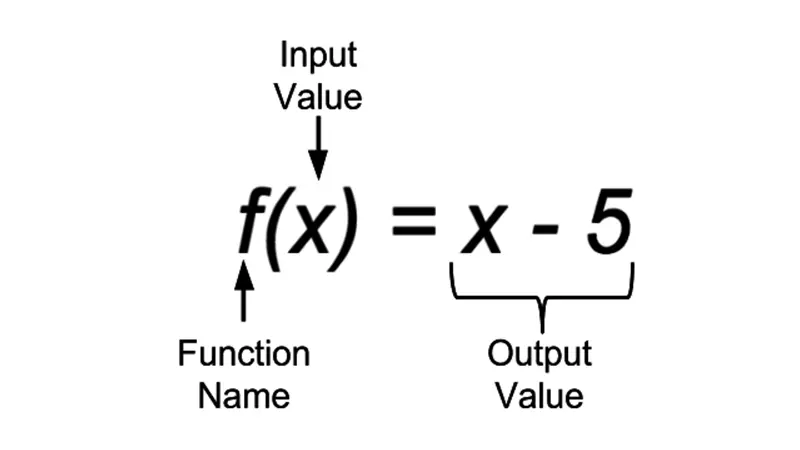
مفهوم الدالة (Function): هي علاقة بين مجموعتين (عادةً من الأعداد)، بحيث يرتبط كل عنصر في المجموعة الأولى (المجال) بعنصر واحد فقط في المجموعة الثانية (المدى). يمكن تصورها كآلة تأخذ مدخلًا واحدًا وتعطي مخرجًا واحدًا فقط.

مكونات الدالة:

المجال (Domain): هي المجموعة التي تحتوي على جميع القيم المدخلة الممكنة للدالة (عادةً قيم المتغير المستقل، غالبًا ما يُرمز له بـ x).
المدى (Range): هي المجموعة التي تحتوي على جميع القيم المخرجة الناتجة عن تطبيق قاعدة الدالة على جميع عناصر المجال (عادةً قيم المتغير التابع، غالبًا ما يُرمز له بـ y أو f(x)).
القاعدة (Rule أو Function Rule): هي القانون أو الصيغة الرياضية التي تحدد كيفية الحصول على قيمة المخرجة (في المدى) لكل قيمة مدخلة (في المجال). غالبًا ما تُكتب على شكل معادلة مثل y=f(x).

تمثيل الدوال: يمكن تمثيل الدوال بثلاث طرق رئيسية:

جبريًا (Algebraically): باستخدام معادلة تربط بين المتغير المستقل (x) والمتغير التابع (y أو f(x)). مثال: f(x)=2x+1.
بيانيًا (Graphically): برسم مجموعة الأزواج المرتبة (x,f(x)) على المستوى الإحداثي. يعطي الرسم البياني تصورًا مرئيًا لسلوك الدالة.
جدوليًا (Tabularly): بعرض مجموعة من القيم المدخلة (x) والقيم المخرجة المقابلة لها (f(x)) في جدول.

أنواع الدوال المختلفة وخصائصها المميزة

تتعدد أنواع الدوال في الرياضيات، ولكل منها خصائص مميزة وسلوك فريد:

الدوال الخطية (Linear Functions): تمثيلها البياني خط مستقيم.
الدوال التربيعية (Quadratic Functions): تمثيلها البياني قطع مكافئ.
الدوال الأسية (Exponential Functions): تصف النمو أو الاضمحلال السريع.
الدوال اللوغاريتمية (Logarithmic Functions): هي معكوس الدوال الأسية.
الدوال المثلثية (Trigonometric Functions): تشمل دوال الجيب (sin)، وجيب التمام (cos)، والظل (tan)، وقاطع التمام (csc)، والقاطع (sec)، وظل التمام (cot). ترتبط بالزوايا والمثلثات الدائرية وتتميز بدورية سلوكها.
الدوال الكسرية (Rational Functions): هي الدوال التي يمكن كتابتها كنسبة بين دالتين كثيرتي حدود.
الدوال الجذرية (Radical Functions): تتضمن جذورًا للمتغير.
الدوال متعددة الحدود (Polynomial Functions): تتكون من حدود جبرية تحتوي على قوى غير سالبة للمتغير.
الدوال المعرفة بأكثر من قاعدة (Piecewise Functions): تُعرف بقواعد مختلفة على أجزاء مختلفة من مجالها.
الدوال الزوجية والفردية (Even and Odd Functions): الدالة الزوجية تحقق (تماثل حول المحور الصادي)، والدالة الفردية تحقق (تماثل حول نقطة الأصل).

خصائص الدوال: تشمل خصائص الدوال مجالها، ومداها، ونقاط تقاطعها مع المحاور، وفترات تزايدها وتناقصها، وقيمها العظمى والصغرى، وسلوكها التقاربي، واستمراريتها، وقابليتها للاشتقاق.

أهمية الدوال وتطبيقاتها الشاملة

تعتبر الدوال لغة أساسية في الرياضيات والعلوم التطبيقية، وتلعب دورًا حاسمًا في نمذجة وتحليل الظواهر المختلفة:

نمذجة الظواهر الطبيعية: تُستخدم الدوال لوصف حركة الأجسام (في الفيزياء)، ونمو الكائنات الحية (في علم الأحياء)، والتفاعلات الكيميائية (في الكيمياء)، والتغيرات المناخية (في علوم الأرض).
تحليل البيانات: تُستخدم الدوال لتمثيل العلاقات بين المتغيرات في مجموعات البيانات وتحليل الاتجاهات والتنبؤ بالقيم المستقبلية (في الإحصاء وعلوم البيانات).
تصميم الأنظمة الهندسية: تُستخدم الدوال في تصميم الدوائر الكهربائية (في الهندسة الكهربائية)، والهياكل الميكانيكية (في الهندسة الميكانيكية)، والعمليات الكيميائية (في الهندسة الكيميائية).
العلوم الاجتماعية والاقتصاد: تُستخدم الدوال لنمذجة سلوك المستهلك والمنتج (في الاقتصاد)، ونمو السكان (في علم الاجتماع)، وانتشار الأمراض (في علم الأوبئة).
علوم الحاسوب: تُستخدم الدوال في البرمجة لتقسيم المهام المعقدة إلى وحدات أصغر قابلة للإدارة وإعادة الاستخدام.
الرسومات الحاسوبية: تُستخدم الدوال الرياضية لرسم المنحنيات والأشكال المعقدة في الرسومات ثنائية وثلاثية الأبعاد.
التشفير: تُستخدم الدوال الرياضية المعقدة في تصميم خوارزميات التشفير لحماية المعلومات.

أمثلة على تطبيقات الدوال:

قانون نيوتن الثاني للحركة: (القوة كدالة للكتلة والتسارع).
نمو السكان الأسي: (عدد السكان كدالة للزمن).
دالة العرض والطلب في الاقتصاد: (الكمية المطلوبة والمعروضة كدالة للسعر).
دوال الموجة في الفيزياء: (وصف حركة الموجات).

الخاتمة

تُمثل الدوال حجر الزاوية في عالم الرياضيات، حيث توفر إطارًا قويًا ومرنًا لوصف وتحليل العلاقات بين الكميات المتغيرة. من خلال فهم أنواعها وخصائصها وطرق تمثيلها، نكتسب القدرة على نمذجة وفهم العالم من حولنا بطريقة رياضية دقيقة. إن تطبيقات الدوال الشاملة في مختلف فروع العلوم والهندسة والتكنولوجيا تؤكد على أهميتها الأساسية كأداة لا غنى عنها في استكشاف الأنماط، والتنبؤ بالسلوك، وحل المشكلات المعقدة التي تواجهنا في سعينا لفهم الكون وتطوير حلول مبتكرة لتحدياته.

تحميل البحث