حجم المنشور

مقدمة

في عالم الهندسة ثلاثية الأبعاد، تُعد المنشورات من الأشكال الهندسية الأساسية التي تتميز ببساطة تركيبها وانتظام قاعدتها وأوجهها الجانبية. فالمنشور هو مجسم له قاعدتان متطابقتان ومتوازيتان، وأوجه جانبية مستطيلة أو متوازية أضلاع تربط بين هاتين القاعدتين. إن فهم مفهوم المنشور وأنواعه المختلفة (مثل المنشور الثلاثي والرباعي والخماسي والمنشور القائم والمنشور المائل)، واستيعاب الطريقة الأساسية لحساب حجمه (مساحة القاعدة مضروبة في الارتفاع)، يمثل خطوة أولى وهامة في استكشاف الفضاء ثلاثي الأبعاد وتطبيقاته الواسعة في الهندسة المعمارية والهندسة المدنية والتصميم الصناعي وغيرها من المجالات العملية.

مفهوم المنشور

هو مجسم ثلاثي الأبعاد يتكون من:

قاعدتين متطابقتين ومتوازيتين: يمكن أن تكونا أي مضلع (مثل مثلث، مربع، مستطيل، خماسي، سداسي، إلخ).
أوجه جانبية: هي أسطح مستوية (إما مستطيلات في المنشور القائم أو متوازيات أضلاع في المنشور المائل) تربط بين حواف القاعدتين المتناظرتين.
ارتفاع (h): هو المسافة العمودية بين القاعدتين المتوازيتين.

أنواع المنشورات

حسب شكل القاعدة:

المنشور الثلاثي: قاعدتاه مثلثان متطابقان ومتوازيان.
المنشور الرباعي: قاعدتاه رباعيان متطابقان ومتوازيان (يشمل متوازي المستطيلات والمكعب والمعين ذي القاعدة المستطيلة).
المنشور الخماسي: قاعدتاه خماسيان متطابقان ومتوازيان.
وهكذا… يمكن أن يكون للمنشور قاعدة على شكل أي مضلع.

حسب زاوية الأوجه الجانبية:

المنشور القائم (Right Prism): تكون أوجهه الجانبية مستطيلات عمودية على القاعدتين. يكون ارتفاع المنشور هو طول أي من أضلاع الأوجه الجانبية العمودية على القاعدة.
المنشور المائل (Oblique Prism): تكون أوجهه الجانبية متوازيات أضلاع مائلة على القاعدتين. يكون ارتفاع المنشور هو المسافة العمودية بين القاعدتين، وليس طول أضلاع الأوجه الجانبية.

طريقة حساب حجم المنشور

حجم أي منشور، بغض النظر عن شكل قاعدته أو ما إذا كان قائمًا أو مائلًا، يُحسب بنفس الطريقة الأساسية:

حجم المنشور (V) = مساحة القاعدة (B) × الارتفاع (h) حيث:

V: يمثل حجم المنشور ويُقاس بوحدات مكعبة (مثل سم³، م³).
B: يمثل مساحة إحدى القاعدتين (بما أنهما متطابقتان) ويُقاس بوحدات مربعة (مثل سم²، م²). يجب حساب مساحة القاعدة بناءً على شكلها (مثل مساحة المثلث = ½ × القاعدة × الارتفاع، مساحة المستطيل = الطول × العرض، مساحة الدائرة = πr² في حالة الأسطوانة التي تعتبر حالة خاصة لمنشور ذي قاعدة دائرية).
h: يمثل ارتفاع المنشور وهو المسافة العمودية بين القاعدتين ويُقاس بوحدات طول (مثل سم، م).

توضيح العلاقة بين مساحة القاعدة والارتفاع والحجم:

يمكن تصور حجم المنشور على أنه عدد الوحدات المكعبة التي يمكن ملء الفراغ الداخلي للمنشور بها. إذا كانت مساحة القاعدة تمثل عدد الوحدات المربعة التي تغطي إحدى القاعدتين، فإن ضرب هذه المساحة في الارتفاع يمثل تكرار هذه الطبقة من الوحدات المربعة بارتفاع المنشور بأكمله، مما ينتج عنه عدد الوحدات المكعبة التي تشغل حيز المنشور.

أمثلة على حساب حجم أنواع مختلفة من المنشورات

– متوازي المستطيلات (منشور رباعي قائم قاعدته مستطيل):

مساحة القاعدة (B) = الطول (l) × العرض (w)
الحجم (V) = l × w × h (حيث h هو الارتفاع)

– المكعب (منشور رباعي قائم قاعدته مربع وأضلاعه متساوية):

مساحة القاعدة (B) = طول الضلع (s) × طول الضلع (s) = s²
الحجم (V) = s² × s = s³

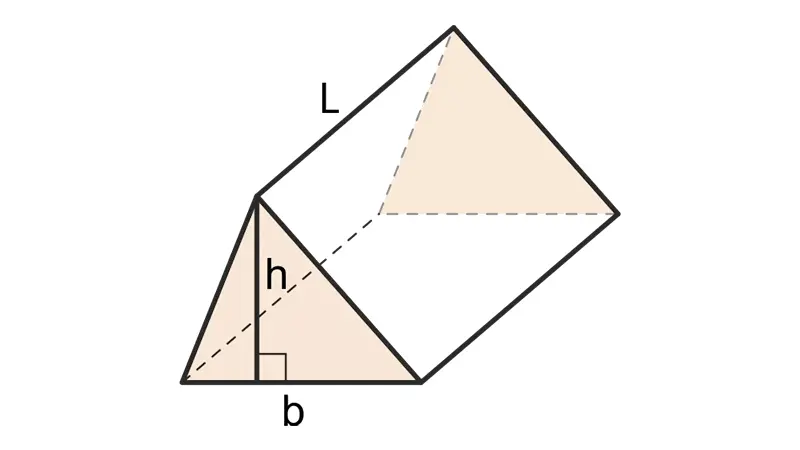
– المنشور الثلاثي القائم:

مساحة القاعدة (B) = ½ × قاعدة المثلث (b’) × ارتفاع المثلث (h’)
الحجم (V) = (½ × b’ × h’) × h (حيث h هو ارتفاع المنشور)

– الأسطوانة القائمة (منشور ذو قاعدة دائرية):

مساحة القاعدة (B) = π × نصف القطر (r)²
الحجم (V) = πr² × h (حيث h هو ارتفاع الأسطوانة)

ملاحظة هامة: عند حساب حجم المنشور المائل، يجب التأكد من استخدام الارتفاع العمودي بين القاعدتين وليس طول الحافة الجانبية المائلة.

أهمية فهم حجم المنشور وتطبيقاته المتنوعة

فهم كيفية حساب حجم المنشور أمرًا بالغ الأهمية وله تطبيقات واسعة في مختلف المجالات:

الهندسة المعمارية والهندسة المدنية:

تقدير كميات المواد اللازمة لبناء هياكل على شكل منشورات (مثل الأعمدة والجسور والأنفاق ذات المقاطع العرضية المنتظمة).
حساب سعات الخزانات والصوامع والقنوات ذات الأشكال المنشورية.
تحديد حجم الحفريات والردم في مشاريع البناء.

التصميم الصناعي والتعبئة والتغليف:

تصميم علب وعبوات ومنتجات ذات أشكال منشورية وحساب سعاتها لتحديد كمية المنتج التي يمكن تعبئتها.
تقدير كمية المواد الخام اللازمة لتصنيع أجزاء ذات أشكال منشورية.
تحسين تصميم المنتجات لتقليل حجمها ووزنها مع الحفاظ على السعة المطلوبة.

الفيزياء والكيمياء:

حساب حجم الأجسام ذات الأشكال المنشورية لتحديد كثافتها أو كمية المادة التي تحتويها.
تقدير حجم السوائل أو الغازات المحفوظة في أوعية منشورية الشكل.
فهم مفاهيم مثل الإزاحة والطفو التي تعتمد على حجم الأجسام المغمورة.

الرياضيات والتعليم:

فهم حجم المنشور هو أساس لفهم مفاهيم الحجوم للأشكال ثلاثية الأبعاد الأكثر تعقيدًا مثل الأهرامات والمخاريط والكرات.
تطوير مهارات التفكير المكاني والتصور ثلاثي الأبعاد لدى الطلاب.
تطبيق المفاهيم الرياضية في حل مشكلات عملية.

علوم الأرض والجيولوجيا:

تقدير حجم الطبقات الصخرية أو الرواسب ذات الأشكال المنشورية التقريبية.
حساب حجم تدفق المياه في قنوات ذات مقاطع عرضية منتظمة.

الخاتمة

يظل مفهوم حجم المنشور وطريقة حسابه من الأساسيات الهامة في عالم الهندسة والأبعاد الثلاثية. ببساطة العلاقة بين مساحة القاعدة والارتفاع، نتمكن من فهم وقياس الفراغ الذي تشغله هذه الأشكال الهندسية المنتظمة، مما يفتح الباب أمام تطبيقات عملية واسعة في مختلف جوانب حياتنا الهندسية والصناعية والعلمية. إن القدرة على تصور المنشور وتحليل أبعاده وحساب حجمه بدقة تمثل مهارة قيمة تساهم في تصميم وبناء عالمنا بكفاءة وفعالية. مع استمرار تطور التكنولوجيا والتصاميم، سيبقى فهم حجم المنشور حجر الزاوية في التعامل مع الفضاء ثلاثي الأبعاد.

تحميل البحث