مقدمة

في عالم الدوال، تحتل الدوال الخطية مكانة أساسية نظرًا لبساطتها وأهميتها في وصف العلاقات التي تتسم بمعدل تغير ثابت. يمكن تصور الدالة الخطية على أنها قاعدة رياضية تنتج تغيرًا منتظمًا في قيمة المخرجات (المتغير التابع) مقابل تغير منتظم في قيمة المدخلات (المتغير المستقل). يتم تمثيل هذه العلاقة بيانيًا بخط مستقيم، وهو أبسط أشكال المنحنيات. إن فهم مفهوم الدالة الخطية وصيغتها القياسية، واستيعاب الطرق المختلفة لتمثيلها بيانيًا (باستخدام الميل والمقطع الصادي الصحيحين، أو من خلال تحديد نقطتين صحيحتين على الخط)، وإدراك أهميتها في وصف وتحليل العلاقات ذات المعدل الثابت في الرياضيات والعلوم التطبيقية، يمثل أساسًا ضروريًا لفهم سلوك الدوال وتطبيقاتها في العديد من المجالات.

مفهوم الدالة الخطية وصيغتها القياسية

مفهوم الدالة الخطية (Linear Function): هي دالة رياضية يمكن تمثيلها بيانيًا بخط مستقيم. تتميز بأن معدل تغير قيمتها (الميل) ثابت.

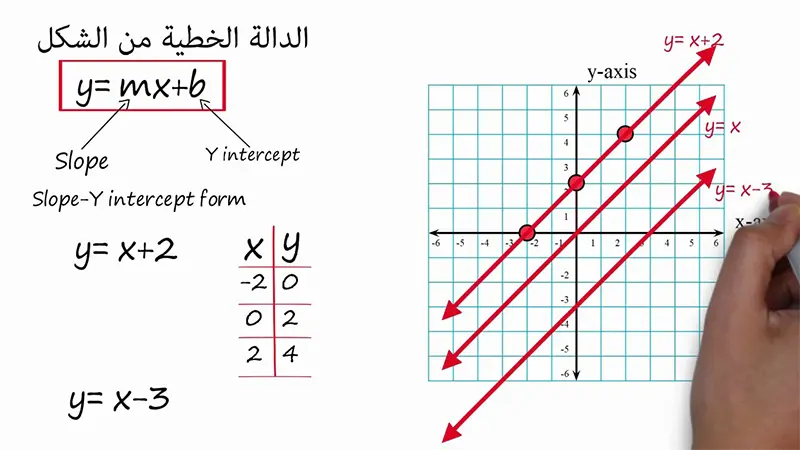
الصيغة القياسية للدالة الخطية (Slope-Intercept Form): تُكتب الدالة الخطية عادةً بالصيغة التالية: y=mx+b حيث:

• y يمثل المتغير التابع (عادةً الإحداثي الصادي على الرسم البياني).
• x يمثل المتغير المستقل (عادةً الإحداثي السيني على الرسم البياني).
• m يمثل ميل الخط (Slope)، وهو مقياس لمدى انحدار الخط واتجاهه. يُحسب الميل بأنه التغير في y لكل وحدة تغير في x بين أي نقطتين مختلفتين على الخط. في هذا البحث، سنركز على الدوال ذات الميل الصحيح.
• b يمثل المقطع الصادي (y-intercept)، وهو قيمة y عندما تكون x=0. بيانيًا، هي النقطة التي يقطع فيها الخط المحور الصادي عند الإحداثيات (0,b). في هذا البحث، سنركز على الدوال ذات المقطع الصادي الصحيح.

حالات خاصة للدوال الخطية:

• الخط الأفقي: يكون ميله صفرًا (m=0) وتكون صيغته y=b (حيث b عدد صحيح).
• الخط الرأسي: لا يمكن كتابته في صيغة الميل والمقطع الصادي، وتكون صيغته x=a (حيث a عدد صحيح ويمثل المقطع السيني).

طرق تمثيل الدوال الخطية بيانيًا باستخدام قيم صحيحة

هناك طريقتان رئيسيتان لتمثيل الدوال الخطية بيانيًا باستخدام قيم صحيحة للميل والمقطع الصادي ونقاط صحيحة على الخط:

استخدام الميل والمقطع الصادي الصحيحين (Using Integer Slope and y-intercept):

1. الخطوة 1: حدد قيمة المقطع الصادي الصحيح (b) من صيغة الدالة (y=mx+b). هذه القيمة تمثل النقطة الأولى على الخط وهي (0,b). قم بتحديد هذه النقطة على المحور الصادي.
2. الخطوة 2: حدد قيمة الميل الصحيح (m) من صيغة الدالة. يمكن تفسير الميل على أنه التغير في y لكل وحدة تغير في x. إذا كان الميل عددًا صحيحًا m, فهذا يعني أنه للانتقال من أي نقطة على الخط إلى نقطة أخرى، يجب التحرك بمقدار m وحدة عموديًا (إلى الأعلى إذا كان m موجبًا وإلى الأسفل إذا كان m سالبًا) ووحدة واحدة إلى اليمين (لتغير x بمقدار موجب واحد).
3. الخطوة 3: ابدأ من النقطة التي تم تحديدها في الخطوة 1 (المقطع الصادي) واستخدم الميل لتحديد نقطة ثانية على الخط ذات إحداثيات صحيحة.
4. الخطوة 4: ارسم خطًا مستقيمًا يمر عبر النقطتين اللتين تم تحديدهما. هذا الخط يمثل الدالة الخطية.

مثال: ارسم الدالة y=2x−3.

• المقطع الصادي b=−3, إذن النقطة الأولى هي (0,−3).
• الميل m=2, إذن من النقطة (0,−3)، تحرك وحدتين إلى الأعلى ووحدة واحدة إلى اليمين للوصول إلى النقطة (1,−1).
• ارسم خطًا مستقيمًا يمر عبر النقطتين (0,−3) و (1,−1).

استخدام نقطتين صحيحتين على الخط (Using Two Integer Points):

1. الخطوة 1: اختر قيمتين صحيحتين مختلفتين لـ x وعوض بهما في صيغة الدالة لإيجاد قيمتي y الصحيحتين المقابلتين. هذا سيعطيك نقطتين على الخط ذات إحداثيات صحيحة، مثل (x1​,y1​) و (x2​,y2​).
2. الخطوة 2: حدد هاتين النقطتين الصحيحتين على المستوى الإحداثي.
3. الخطوة 3: ارسم خطًا مستقيمًا يمر عبر هاتين النقطتين. هذا الخط يمثل الدالة الخطية.

مثال: ارسم الدالة y=−x+5.

• إذا كانت x=0, فإن y=−(0)+5=5, إذن النقطة الأولى هي (0,5).
• إذا كانت x=3, فإن y=−(3)+5=2, إذن النقطة الثانية هي (3,2).
• ارسم خطًا مستقيمًا يمر عبر النقطتين (0,5) و (3,2).

أهمية تمثيل الدوال الخطية وتطبيقاتها المتنوعة

يعد تمثيل الدوال الخطية بيانيًا باستخدام قيم صحيحة أداة قوية وضرورية لفهم وتحليل العلاقات ذات المعدل الثابت ولها تطبيقات واسعة في مختلف المجالات:

• تصور العلاقات الخطية: يساعد الرسم البياني للدالة الخطية في تصور العلاقة بين المتغيرين وفهم كيفية تغير أحدهما بالنسبة للآخر بمعدل ثابت باستخدام وحدات صحيحة.
• تحديد الميل والمقطع الصادي بصريًا: من خلال الرسم البياني، يمكن تحديد ميل الخط (من خلال التغير الرأسي لوحدة التغير الأفقي) والمقطع الصادي (نقطة تقاطع الخط مع المحور الصادي) بسهولة باستخدام قيم صحيحة.
• حل المعادلات الخطية: يمكن إيجاد حل نظام من معادلتين خطيتين بتمثيل كل معادلة بيانيًا ونقطة تقاطع الخطين تمثل الحل المشترك (إذا كانت نقطة التقاطع ذات إحداثيات صحيحة).
• نمذجة الظواهر ذات المعدل الثابت في العلوم:
  • الفيزياء: وصف الحركة المنتظمة (المسافة كدالة للزمن بسرعات صحيحة).
  • الكيمياء: وصف بعض التغيرات التي تحدث بمعدلات صحيحة.
  • الأحياء: وصف النمو الخطي بوحدات صحيحة.

• التطبيقات في الاقتصاد والمالية:
  • التكلفة الخطية: تمثيل التكلفة الكلية بوحدات صحيحة.
  • الربح والخسارة الخطية: نمذجة بسيطة للعلاقة بين الإيرادات والتكاليف.
• تحليل البيانات: يمكن استخدام الخطوط المستقيمة ذات الميل والمقطع الصادي الصحيحين لتقريب البيانات التي تظهر اتجاهًا خطيًا بوحدات صحيحة.
• البرمجة وعلوم الحاسوب: تستخدم الدوال الخطية ذات القيم الصحيحة في العديد من الخوارزميات والرسومات الحاسوبية البسيطة.

أمثلة على تطبيقات تمثيل الدوال الخطية بقيم صحيحة:

• حساب المسافة المقطوعة بواسطة قطار يسير بسرعة ثابتة: إذا كان قطار يسير بسرعة 30 كيلومترًا في الساعة، فإن العلاقة بين المسافة والزمن هي دالة خطية d=30t, حيث الميل يمثل السرعة الصحيحة.
• تحديد تكلفة شراء عدد من الأقلام بسعر ثابت للقلم الواحد ورسوم توصيل ثابتة: إذا كان سعر القلم الواحد 2 دولار ورسوم التوصيل الثابتة 5 دولارات، فإن التكلفة الكلية هي دالة خطية C=2n+5, حيث الميل يمثل السعر الصحيح للقلم والمقطع الصادي يمثل رسوم التوصيل الصحيحة.

الخاتمة

يعد تمثيل الدوال الخطية بيانيًا باستخدام قيم صحيحة أداة أساسية لفهم وتصور العلاقات التي تتسم بمعدل تغير ثابت بوحدات صحيحة. من خلال استخدام الميل والمقطع الصادي الصحيحين أو تحديد نقطتين صحيحتين على الخط، يمكننا رسم هذه الدوال وتحليل سلوكها واستخدامها في نمذجة العديد من الظواهر في الرياضيات والعلوم التطبيقية بطريقة مبسطة. إن بساطة الدوال الخطية ذات القيم الصحيحة وقدرتها على وصف العلاقات الأساسية تجعلها لبنة هامة في بناء فهم أعمق لعالم الدوال وتطبيقاتها المتنوعة.