مقدمة

في عالم الرياضيات، لا تقتصر العلاقات بين الكميات على المساواة فحسب؛ ففي كثير من الأحيان، نحتاج إلى وصف حالات تكون فيها كمية أكبر أو أصغر من أخرى. هنا يأتي دور المتباينات (Inequalities)، وهي عبارات رياضية تُعبر عن عدم التساوي بين قيمتين أو تعبيرين. بينما تُستخدم المعادلات لإيجاد قيمة محددة للمتغير، تُستخدم المتباينات لتحديد مجموعة من القيم التي يُمكن أن يتخذها المتغير. تُعد المتباينات بالجمع والطرح من أبسط أنواع المتباينات، وتُمثل نقطة الانطلاق لفهم التعامل مع العلاقات اللامتساوية بشكل أكثر تعقيدًا. إن إتقان هذه المهارة ليس ضروريًا فقط في الجبر، بل هو أساس لتفسير الظواهر الواقعية التي تتضمن قيودًا أو حدودًا، مثل الميزانيات، حدود السرعة، أو درجات الحرارة. تُوفر لنا هذه المتباينات أداة قوية لوصف وتحليل المواقف التي لا تكون فيها الكميات متطابقة تمامًا، بل ترتبط بعلاقات تفوق أو نقص.

مفهوم المتباينة وعلاماتها

المتباينة (Inequality): هي عبارة رياضية تُقارن بين قيمتين أو تعبيرين باستخدام إحدى علامات عدم التساوي. على عكس المعادلة التي تحتوي على علامة المساواة (=)، فإن المتباينة تُشير إلى أن قيمة ما قد تكون أكبر من، أصغر من، أكبر من أو تساوي، أو أصغر من أو تساوي قيمة أخرى.

علامات المتباينة:

• أصغر من (<): تُستخدم للإشارة إلى أن القيمة الموجودة على اليسار أقل من القيمة الموجودة على اليمين.
  • مثال: 5 < 8 (خمسة أصغر من ثمانية).
• أكبر من (>): تُستخدم للإشارة إلى أن القيمة الموجودة على اليسار أكبر من القيمة الموجودة على اليمين.
  • مثال: 10 > 3 (عشرة أكبر من ثلاثة).
• أصغر من أو تساوي (≤): تُستخدم للإشارة إلى أن القيمة الموجودة على اليسار أقل من أو تساوي القيمة الموجودة على اليمين.
  • مثال: س ≤ 7 (س أصغر من أو تساوي سبعة).
• أكبر من أو تساوي (≥): تُستخدم للإشارة إلى أن القيمة الموجودة على اليسار أكبر من أو تساوي القيمة الموجودة على اليمين.
  • مثال: ص ≥ 2 (ص أكبر من أو تساوي اثنين).
• لا يساوي (≠): تُستخدم للإشارة إلى أن القيمتين ليستا متساويتين. تُعامل هذه المتباينة بشكل مختلف عن الأنواع الأربعة الأخرى، حيث يكون حلها عادةً كل الأعداد الحقيقية باستثناء قيمة واحدة أو أكثر.
  • مثال: س ≠ 4 (س لا تساوي أربعة).

المجال (Domain) والحل (Solution):

• حل المتباينة ليس قيمة واحدة عادةً، بل هو مجموعة من القيم التي تجعل المتباينة صحيحة.
• تمثل مجموعة الحل غالبًا باستخدام الترميز الفتري أو بالتمثيل البياني على خط الأعداد.

خصائص المتباينات الأساسية

تُشبه المتباينات المعادلات في كثير من خصائصها، ولكن هناك فرق حاسم يجب الانتباه إليه عند الضرب أو القسمة على عدد سالب.

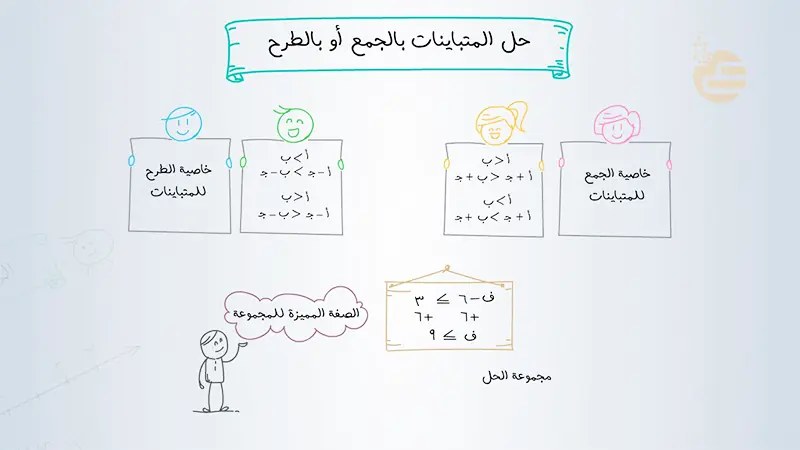
1. خاصية الإضافة (الجمع): إذا أضفنا نفس الكمية إلى كلا طرفي المتباينة، فإن اتجاه المتباينة لا يتغير.
   • إذا كان أ < ب، فإن أ + ج < ب + ج.
   • مثال: إذا كان 3 < 5، فإن 3 + 2 < 5 + 2، أي 5 < 7 (صحيح).
2. خاصية الطرح: إذا طرحنا نفس الكمية من كلا طرفي المتباينة، فإن اتجاه المتباينة لا يتغير.
   • إذا كان أ < ب، فإن أ – ج < ب – ج.
   • مثال: إذا كان 10 > 6، فإن 10 – 4 > 6 – 4، أي 6 > 2 (صحيح).
3. خاصية الضرب والقسمة (مع الأعداد الموجبة): إذا ضربنا أو قسمنا كلا طرفي المتباينة على نفس الكمية الموجبة، فإن اتجاه المتباينة لا يتغير.
   • إذا كان أ < ب و ج > 0، فإن أ مضروبة في ج < ب مضروبة في ج، وأ مقسومة على ج < ب مقسومة على ج.
   • مثال: إذا كان 2 < 4، فإن 2 مضروبة في 3 < 4 مضروبة في 3، أي 6 < 12 (صحيح).
4. خاصية الضرب والقسمة (مع الأعداد السالبة): إذا ضربنا أو قسمنا كلا طرفي المتباينة على نفس الكمية السالبة، فإن اتجاه المتباينة ينعكس.
   • إذا كان أ < ب و ج < 0، فإن أ مضروبة في ج > ب مضروبة في ج، وأ مقسومة على ج > ب مقسومة على ج.
   • مثال: إذا كان 2 < 4، وضربنا في سالب 3: 2 مضروبة في سالب 3 هي سالب 6، و 4 مضروبة في سالب 3 هي سالب 12. يجب أن نعكس العلامة لتصبح: سالب 6 > سالب 12 (صحيح).

حل المتباينات بالجمع أو الطرح

يُعد حل المتباينات بالجمع أو الطرح من أبسط أنواع المتباينات ذات الخطوة الواحدة. الهدف هو عزل المتغير في أحد طرفي المتباينة، تمامًا كما نفعل في المعادلات، ولكن مع الأخذ في الاعتبار الحفاظ على اتجاه المتباينة.

الخطوات الأساسية:

1. تحديد المتغير: ابحث عن المتغير الذي تريد عزله.
2. تحديد العدد الثابت: ابحث عن العدد الثابت الموجود في نفس طرف المتغير.
3. استخدام العملية العكسية:
   • إذا كان العدد الثابت مضافًا إلى المتغير، قم بطرح هذا العدد من كلا طرفي المتباينة.
   • إذا كان العدد الثابت مطروحًا من المتغير، قم بإضافة هذا العدد إلى كلا طرفي المتباينة.
4. الحفاظ على اتجاه المتباينة: تذكر أن عمليتي الجمع والطرح لا تُغيران اتجاه علامة المتباينة.

أمثلة توضيحية:

مثال 1: حل متباينة بالجمع

حل المتباينة: س ناقص 5 أصغر من 10

1. المتغير هو س، والعدد الثابت في نفس الطرف هو سالب 5.
2. نستخدم العملية العكسية للطرح، وهي الجمع. نضيف 5 إلى كلا طرفي المتباينة. س ناقص 5 زائد 5 أصغر من 10 زائد 5 س أصغر من 15
3. مجموعة الحل: جميع الأعداد التي هي أصغر من 15.
   • التمثيل البياني على خط الأعداد: نرسم دائرة مفتوحة عند 15 وخط يتجه إلى اليسار (باتجاه الأعداد الأصغر).
   • الترميز الفتري: (سالب ما لا نهاية، 15).

مثال 2: حل متباينة بالطرح

حل المتباينة: ص زائد 3 أكبر من أو تساوي 8

1. المتغير هو ص، والعدد الثابت في نفس الطرف هو موجب 3.
2. نستخدم العملية العكسية للجمع، وهي الطرح. نطرح 3 من كلا طرفي المتباينة. ص زائد 3 ناقص 3 أكبر من أو تساوي 8 ناقص 3 ص أكبر من أو تساوي 5
3. مجموعة الحل: جميع الأعداد التي هي أكبر من أو تساوي 5.
   • التمثيل البياني على خط الأعداد: نرسم دائرة مغلقة (مظللة) عند 5 وخط يتجه إلى اليمين (باتجاه الأعداد الأكبر).
   • الترميز الفتري: [5، موجب ما لا نهاية).

مثال 3: متباينة مع عدد سالب (توضيح لعدم عكس العلامة)

حل المتباينة: س ناقص 7 أكبر من سالب 2

1. المتغير هو س، والعدد الثابت هو سالب 7.
2. نضيف 7 إلى كلا طرفي المتباينة. س ناقص 7 زائد 7 أكبر من سالب 2 زائد 7 س أكبر من 5
3. مجموعة الحل: جميع الأعداد التي هي أكبر من 5.
   • التمثيل البياني: دائرة مفتوحة عند 5 وخط يتجه إلى اليمين.
   • الترميز الفتري: (5، موجب ما لا نهاية). لاحظ أننا لم نعكس علامة المتباينة لأننا قمنا بعملية جمع.

تمثيل مجموعة الحل على خط الأعداد

يُعد التمثيل البياني لمجموعة الحل على خط الأعداد طريقة مرئية وواضحة لفهم النطاق الذي يشمله حل المتباينة.

قواعد التمثيل البياني:

1. تحديد نقطة البداية: تُحدد هذه النقطة بالعدد الثابت في حل المتباينة.
2. نوع الدائرة:
   • دائرة مفتوحة (غير مظللة): تُستخدم عندما تكون علامة المتباينة (<) أو (>) (أي أن العدد نفسه ليس جزءًا من الحل).
   • دائرة مغلقة (مظللة): تُستخدم عندما تكون علامة المتباينة (≤) أو (≥) (أي أن العدد نفسه جزء من الحل).
3. اتجاه السهم:
   • سهم يتجه لليمين: يُستخدم عندما تكون علامة المتباينة (>) أو (≥) (تُشير إلى الأعداد الأكبر).
   • سهم يتجه لليسار: يُستخدم عندما تكون علامة المتباينة (<) أو (≤) (تُشير إلى الأعداد الأصغر).

مثال: لتمثيل حل المتباينة س أصغر من 15: نضع دائرة مفتوحة عند النقطة 15 على خط الأعداد، ثم نرسم سهمًا يتجه من 15 إلى اليسار.

مثال: لتمثيل حل المتباينة ص أكبر من أو تساوي 5: نضع دائرة مغلقة عند النقطة 5 على خط الأعداد، ثم نرسم سهمًا يتجه من 5 إلى اليمين.

تطبيقات المتباينات في الحياة الواقعية

تُعد المتباينات أدوات أساسية لوصف القيود، الحدود، والشروط في مواقف الحياة اليومية والعديد من المجالات العلمية والمهنية:

1. الميزانيات والمالية: تحديد المبلغ الأقصى الذي يمكن إنفاقه، أو الحد الأدنى للإيرادات المطلوبة.
   • مثال: إذا كان لديك 200 دولار، وتريد شراء كتاب بسعر 30 دولارًا، فكم يمكن أن تنفق على ملابس؟ 200 ناقص 30 أكبر من أو تساوي س (المبلغ المتبقي للملابس). 170 أكبر من أو تساوي س، أو س أصغر من أو تساوي 170. يمكنك إنفاق 170 دولارًا أو أقل على الملابس.
2. السرعة والمسافة: قيود السرعة القصوى أو الدنيا.
   • مثال: يجب أن تكون سرعة السيارة (س) أقل من أو تساوي 100 كيلومتر في الساعة. س ≤ 100.
3. درجة الحرارة: نطاقات درجات الحرارة الآمنة أو التشغيلية.
   • مثال: لتشغيل جهاز معين، يجب أن تكون درجة الحرارة (د) أكبر من 0 درجة مئوية. د > 0.
4. الكميات والمخزون: تحديد الكميات الدنيا أو القصوى للمنتجات.
   • مثال: يجب أن يكون عدد الوحدات في المخزون (و) أكبر من 500 وحدة لتجنب النقص. و > 500.
5. الصحة والتغذية: الجرعات الموصى بها للأدوية أو المدخول اليومي من العناصر الغذائية.
   • مثال: يجب أن تستهلك ما لا يقل عن 2000 سعر حراري يوميًا (س). س ≥ 2000.

الخاتمة

تُعد المتباينات بالجمع أو الطرح اللبنة الأساسية لفهم العلاقات اللامتساوية في الرياضيات. فبينما تُخبرنا المعادلات عن “ماذا”، تُخبرنا المتباينات عن “إلى أي مدى” أو “في أي نطاق”. إن إتقان كيفية عزل المتغير في هذه المتباينات، مع الحفاظ على اتجاه العلامة، يُمثل خطوة حاسمة نحو حل متباينات أكثر تعقيدًا وتفسير مجموعات الحلول المتنوعة. تتجاوز أهمية المتباينات مجرد كونها مفهومًا جبريًا؛ فهي تُشكل أداة تحليلية قوية لوصف القيود، وتحديد النطاقات، وفهم الشروط في سياقات حياتنا اليومية والعلمية. تُمكننا هذه المهارة من التفكير بشكل أكثر مرونة حول العلاقات الكمية، وتُعزز قدرتنا على اتخاذ قرارات مستنيرة ضمن الحدود المعطاة.