مقدمة

في علم الهندسة، تُعتبر التحويلات الهندسية أدوات قوية لتغيير موقع أو حجم أو شكل الأشكال الهندسية. لقد تناولنا في أبحاث سابقة بعضًا من هذه التحويلات الأساسية مثل الإزاحة والانعكاس والدوران والتمدد. ولكن في كثير من الأحيان، لا يتم تطبيق تحويل واحد فقط على شكل ما، بل قد يتم تطبيق سلسلة من التحويلات المتتابعة. هذه العملية تُعرف باسم تركيب التحويلات الهندسية، وهي مفهوم أساسي يسمح لنا بإنشاء تحويلات أكثر تعقيدًا وتنوعًا. إن فهم تركيب التحويلات الهندسية وخصائصه وتأثيره يُعد أمرًا بالغ الأهمية في العديد من المجالات مثل الرسومات الحاسوبية والتحريك والروبوتات والتصميم الهندسي.

تعريف تركيب التحويلات الهندسية وكيفية تطبيقه

تركيب التحويلات الهندسية يعني تطبيق تحويل هندسي على شكل ما، ثم تطبيق تحويل هندسي آخر على الصورة الناتجة من التحويل الأول، وهكذا. بمعنى آخر، هو تطبيق تحويلين أو أكثر بشكل متتابع على نفس الشكل.

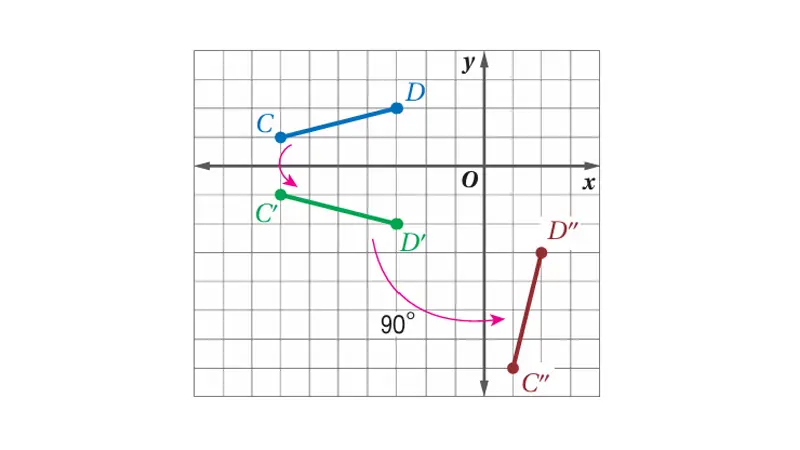
لتوضيح ذلك، إذا كان لدينا شكل أصلي (أ) وتم تطبيق التحويل الهندسي الأول (ت₁) عليه، فإننا نحصل على صورة جديدة (أ’). ثم إذا قمنا بتطبيق التحويل الهندسي الثاني (ت₂) على الصورة (أ’)، فإننا نحصل على الصورة النهائية (أ”). يمكن التعبير عن هذه العملية بالقول بأن التحويل الذي ينقل الشكل (أ) مباشرة إلى الشكل (أ”) هو تركيب التحويلين (ت₁) ثم (ت₂)، ويُكتب عادةً بالرمز ت₂ ∘ ت₁.

من المهم ملاحظة أن ترتيب تطبيق التحويلات مهم جدًا في عملية التركيب. ففي الغالب، تطبيق التحويل (ت₁) ثم (ت₂) ينتج عنه صورة نهائية مختلفة عن تطبيق التحويل (ت₂) ثم (ت₁). هذا يعني أن تركيب التحويلات ليس عملية تبديلية بشكل عام.

خصائص تركيب التحويلات الهندسية

يتمتع تركيب التحويلات الهندسية بعدة خصائص هامة:

1. الترابطية: إذا كان لدينا ثلاثة تحويلات هندسية (ت₁، ت₂، ت₃)، فإن تركيب (ت₂ ∘ ت₁) ثم (ت₃) هو نفسه تركيب (ت₂) ثم (ت₃ ∘ ت₁). أي أن (ت₃ ∘ (ت₂ ∘ ت₁)) = ((ت₃ ∘ ت₂) ∘ ت₁). هذه الخاصية تسمح لنا بتجميع التحويلات بأي ترتيب عند تطبيقها بشكل متتابع.
2. وجود التحويل المحايد: يوجد تحويل هندسي يُسمى التحويل المحايد (أو التطابق)، والذي لا يُغير من موقع أو شكل أي نقطة. عند تركيب أي تحويل مع التحويل المحايد، فإن النتيجة تكون التحويل الأصلي نفسه.
3. وجود التحويل العكسي: لكل تحويل هندسي (في الغالب) تحويل عكسي يقوم بإعادة الصورة إلى الشكل الأصلي. عند تركيب تحويل مع تحويله العكسي، فإن النتيجة تكون التحويل المحايد.
4. الحفاظ على خصائص التحويلات المكونة: يعتمد نوع وخصائص التحويل الناتج عن التركيب على أنواع وخصائص التحويلات التي تم تركيبها. على سبيل المثال، تركيب تحويلين يحافظان على التطابق (مثل الإزاحة والانعكاس والدوران) ينتج عنه تحويل يحافظ أيضًا على التطابق.

تركيب أكثر من تحويلين هندسيين

يمكن تطبيق عملية التركيب على أكثر من تحويلين هندسيين بشكل متتابع. في هذه الحالة، يتم تطبيق التحويل الأول على الشكل الأصلي، ثم يتم تطبيق التحويل الثاني على الصورة الناتجة، وهكذا حتى يتم تطبيق جميع التحويلات المطلوبة. كما ذكرنا سابقًا، فإن ترتيب تطبيق هذه التحويلات يلعب دورًا حاسمًا في تحديد الصورة النهائية.

أمثلة على تركيب تحويلين هندسيين

لفهم عملية تركيب التحويلات بشكل أفضل، إليك بعض الأمثلة:

1. تركيب إزاحتين: إذا قمنا بإزاحة شكل ما بمتجه (أ، ب)، ثم قمنا بإزاحة الصورة الناتجة بمتجه (ج، د)، فإن النتيجة النهائية هي إزاحة واحدة بمتجه (أ + ج، ب + د).
2. تركيب انعكاسين:
   • انعكاس حول مستقيمين متوازيين: تركيب انعكاس حول مستقيمين متوازيين ينتج عنه إزاحة في اتجاه عمودي على المستقيمين وبمسافة تساوي ضعف المسافة بينهما.
   • انعكاس حول مستقيمين متقاطعين: تركيب انعكاس حول مستقيمين متقاطعين ينتج عنه دوران حول نقطة تقاطع المستقيمين بزاوية تساوي ضعف الزاوية بين المستقيمين.
3. تركيب دورانين: إذا قمنا بتدوير شكل ما حول نقطة معينة بزاوية θ₁، ثم قمنا بتدوير الصورة الناتجة حول نفس النقطة بزاوية θ₂، فإن النتيجة النهائية هي دوران واحد حول نفس النقطة بزاوية θ₁ + θ₂.
4. تركيب إزاحة ودوران: تركيب إزاحة ودوران (أو دوران وإزاحة) ينتج عنه ما يُعرف باسم الدوران المنزلق (Rototranslation) أو في حالات خاصة الانعكاس المنزلق (Glide Reflection).
5. تركيب دوران وانعكاس: تركيب دوران وانعكاس (أو انعكاس ودوران) ينتج عنه انعكاس حول مستقيم آخر.

الأيزومترية وتركيب التحويلات

الأيزومترية هي التحويلات الهندسية التي تحافظ على المسافات بين النقاط، وبالتالي تحافظ على شكل وحجم الشكل الأصلي. تشمل الأيزومترية الإزاحة والانعكاس والدوران. عند تركيب أي عدد من التحويلات الأيزومترية، فإن التحويل الناتج يكون أيضًا أيزومترية. هذا يعني أن الصورة النهائية الناتجة عن تركيب أي عدد من الإزاحات والانعكاسات والدورانات ستكون مطابقة تمامًا للشكل الأصلي من حيث الشكل والحجم.

تطبيقات تركيب التحويلات الهندسية

1. الرسومات الحاسوبية والتحريك: في هذا المجال، يتم استخدام تركيب التحويلات الهندسية لإنشاء حركات معقدة للأجسام والشخصيات في الرسوم المتحركة وألعاب الفيديو. على سبيل المثال، يمكن تحريك شخصية ما (إزاحة)، وتدوير ذراعها (دوران)، وتغيير حجمها (تمدد) في نفس الوقت أو بشكل متتابع باستخدام تركيب التحويلات.
2. علم الروبوتات: تعتمد حركة الروبوتات على سلسلة من الإزاحات والدورانات التي يتم تركيبها لتحقيق الحركة المطلوبة للروبوت وأجزائه المختلفة.
3. التصنيع والautomation: في عمليات التصنيع الآلية، يتم استخدام تركيب التحويلات الهندسية لتحريك وتجميع الأجزاء بدقة وكفاءة.
4. تطوير الألعاب: يتم استخدام تركيب التحويلات الهندسية لتحريك الكائنات وتغيير مواقعها وتدويرها في بيئة اللعبة.
5. الفنون والتصميم: يستخدم الفنانون والمصممون تركيب التحويلات الهندسية لإنشاء أنماط وزخارف معقدة ومتكررة، مثل استخدام الانعكاس والدوران لإنشاء رسومات متناظرة.
6. تحليل الحركة في الفيزياء: يمكن تحليل حركة الأجسام المعقدة على أنها تركيب لمجموعة من الإزاحات والدورانات.

تمثيل تركيب التحويلات باستخدام المصفوفات

في الرياضيات المتقدمة، يمكن تمثيل التحويلات الهندسية باستخدام المصفوفات. وعند تمثيل التحويلات باستخدام المصفوفات، فإن تركيب تحويلين هندسيين يتم تمثيله بضرب مصفوفتي التحويلين. هذا يوفر طريقة فعالة ومنظمة لتنفيذ وتحليل تركيب التحويلات، خاصة عند التعامل مع سلاسل طويلة من التحويلات.

خاتمة

تركيب التحويلات الهندسية هو مفهوم أساسي وهام في علم الهندسة يسمح لنا بإنشاء تحويلات أكثر تعقيدًا من خلال تطبيق تحويلين أو أكثر بشكل متتابع. لقد استعرضنا في هذا البحث تعريف تركيب التحويلات وخصائصه وأهميته، بالإضافة إلى استعراض أمثلة متنوعة وتطبيقات عملية لهذا المفهوم في مختلف المجالات. إن فهم كيفية تركيب التحويلات الهندسية يفتح لنا آفاقًا واسعة في فهم وتصميم وإنشاء الأشكال والحركات المعقدة في عالمنا الرقمي والفيزيائي. فتركيب التحويلات، ببساطة، هو لغة الهندسة الحديثة التي تتيح لنا التعبير عن التغيير والحركة بطرق دقيقة وفعالة.