علاقات الزوايا والمستقيمات

مقدمة

تُعد الزوايا والمستقيمات من اللبنات الأساسية في علم الهندسة الإقليدية، الذي يصف الفضاء الذي ندركه ونعيش فيه. إن فهم العلاقات بين هذه الكيانات الهندسية يُعتبر حجر الزاوية في دراسة الأشكال والمجسمات والقياسات، ويمتد تأثيره ليشمل تطبيقات واسعة في مجالات متنوعة كالهندسة المعمارية، والتصميم، والفيزياء، والهندسة، وعلوم الحاسوب، وحتى الفنون. فمن خلال إدراك كيف تتشكل الزوايا عند تقاطع المستقيمات، وكيف تتوازى المستقيمات أو تتعامد، وكيف تتكون الأشكال الهندسية المختلفة، نتمكن من تحليل الهياكل، وتصميم الأبنية، وفهم حركة الأجسام، وتطوير الخوارزميات، وتقدير الجماليات البصرية. إن استيعاب العلاقات بين الزوايا والمستقيمات يفتح لنا نافذة على النظام الدقيق الذي يحكم الكون من حولنا، ويُمكننا من التفاعل معه بأسس رياضية واضحة.

المفاهيم الأساسية للزوايا والمستقيمات

المستقيم (Line): هو مسار لا نهاية له في كلا الاتجاهين، ويتكون من عدد لا نهائي من النقاط. يُمكن تحديده بنقطتين مختلفتين تقعان عليه.
القطعة المستقيمة (Line Segment): هي جزء من المستقيم محدد بنقطتين نهايتين.
الشعاع (Ray): هو جزء من المستقيم له نقطة بداية واحدة ويمتد بلا نهاية في اتجاه واحد.
الزاوية (Angle): هي الشكل الناتج عن التقاء شعاعين لهما نفس نقطة البداية (رأس الزاوية). تُقاس الزوايا عادة بالدرجات (°).

أنواع الزوايا وعلاقاتها

تُصنف الزوايا بناءً على قياسها، كما توجد علاقات خاصة بين أزواج الزوايا:

أنواع الزوايا حسب القياس:

زاوية حادة (Acute Angle): قياسها أكبر من 0° وأقل من 90°.
زاوية قائمة (Right Angle): قياسها يساوي 90°.
زاوية منفرجة (Obtuse Angle): قياسها أكبر من 90° وأقل من 180°.
زاوية مستقيمة (Straight Angle): قياسها يساوي 180°.
زاوية منعكسة (Reflex Angle): قياسها أكبر من 180° وأقل من 360°.
زاوية كاملة (Full Angle): قياسها يساوي 360°.

علاقات بين أزواج الزوايا:

الزاويتان المتجاورتان:هما زاويتان تشتركان في رأس وضلع واحد، ولكنهما لا تتداخلان.
الزاويتان المتقابلتان بالرأس: هما زاويتان ناتجتان عن تقاطع مستقيمين، وكل زاوية تقابل الأخرى بالرأس وتكونان متساويتين في القياس.
الزاويتان المتكاملتان: هما زاويتان يكون مجموع قياسهما 180°.
الزاويتان المتتامّتان: هما زاويتان يكون مجموع قياسهما 90°.

علاقات المستقيمات

تتعدد العلاقات بين المستقيمات في المستوى، وأهمها:

المستقيمان المتوازيان (Parallel Lines): هما مستقيمان يقعان في نفس المستوى ولا يتقاطعان أبدًا، والمسافة بينهما ثابتة. يُرمز للتوازي بالرمز ∥.
المستقيمان المتعامدان (Perpendicular Lines): هما مستقيمان يتقاطعان بزاوية قائمة (90°). يُرمز للتعامد بالرمز ⊥.
المستقيمان المتقاطعان (Intersecting Lines): هما مستقيمان يشتركان في نقطة واحدة.

العلاقات بين الزوايا والمستقيمات المتوازية والقاطع

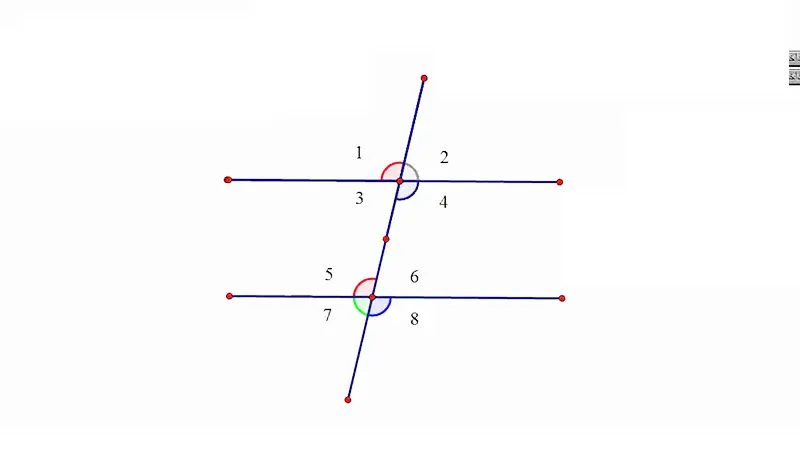
عندما يقطع مستقيم ثالث (يُسمى القاطع) مستقيمين متوازيين، تتكون أزواج من الزوايا ذات علاقات خاصة:

الزاويتان المتبادلتان داخليًا (Alternate Interior Angles): هما زاويتان تقعان على جهتين مختلفتين من القاطع وداخل المستقيمين المتوازيين، وهما متساويتان في القياس.
الزاويتان المتبادلتان خارجيًا (Alternate Exterior Angles): هما زاويتان تقعان على جهتين مختلفتين من القاطع وخارج المستقيمين المتوازيين، وهما متساويتان في القياس.
الزاويتان المتناظرتان (Corresponding Angles): هما زاويتان تقعان على نفس الجهة من القاطع، إحداهما داخل المستقيمين المتوازيين والأخرى خارجهما، وهما متساويتان في القياس.
الزاويتان المتحالفتان: هما زاويتان تقعان على نفس الجهة من القاطع وداخل المستقيمين المتوازيين، وهما متكاملتان (مجموع قياسهما 180°).

الخصائص الهندسية الناتجة عن علاقات الزوايا والمستقيمات

تنتج عن العلاقات بين الزوايا والمستقيمات خصائص هندسية هامة تُستخدم في بناء الأشكال الهندسية وتحليلها:

في المثلثات: مجموع قياسات الزوايا الداخلية للمثلث يساوي 180°. في المثلث المتساوي الأضلاع تكون جميع الزوايا متساوية (60°). في المثلث المتساوي الساقين تكون زاويتا القاعدة متساويتين.
في الرباعيات: مجموع قياسات الزوايا الداخلية للرباعي يساوي 360°. في متوازي الأضلاع تكون كل زاويتين متقابلتين متساويتين، وكل زاويتين متجاورتين متكاملتين. في المستطيل تكون جميع الزوايا قائمة. في المربع تكون جميع الزوايا قائمة وجميع الأضلاع متساوية.
في المضلعات المنتظمة: تكون جميع الزوايا متساوية وجميع الأضلاع متساوية.

تطبيقات علاقات الزوايا والمستقيمات في مجالات متنوعة

تتعدد تطبيقات علاقات الزوايا والمستقيمات في شتى المجالات، ومن أبرزها:

الهندسة المعمارية والتصميم: تحديد الزوايا بين الجدران والأسقف، وضمان توازي الأعمدة وتعامدها، وتصميم الواجهات بزوايا جمالية ووظيفية.
الهندسة المدنية والإنشاء: تخطيط الطرق والجسور والأنفاق بزوايا محددة، وضمان استقامة الهياكل وتوازنها.
الفيزياء: تحليل حركة المقذوفات بزوايا الإطلاق، ودراسة انعكاس وانكسار الضوء بزوايا محددة، وتحليل القوى المتجهة بزوايا تأثيرها.
الهندسة الميكانيكية: تصميم الآلات والمحركات بأجزاء تتحرك بزوايا دقيقة، وضمان عمل التروس والوصلات بشكل صحيح.
علوم الحاسوب والرسومات: بناء النماذج ثلاثية الأبعاد وتدويرها وتحريكها باستخدام مفاهيم الزوايا، وتحديد مواقع العناصر في الفضاء ثنائي وثلاثي الأبعاد.
الفنون والتصوير: تكوين المشاهد بزوايا رؤية مختلفة لإحداث تأثيرات بصرية متنوعة، واستخدام الزوايا في تصميم اللوحات والمنحوتات.
الملاحة وعلم الفلك: تحديد المواقع والاتجاهات باستخدام الزوايا بين الأجرام السماوية والأفق.

الخاتمة

إن العلاقات بين الزوايا والمستقيمات هي أسس راسخة في علم الهندسة الإقليدية، وهي بمثابة اللغة التي تصف وتُنظم الأشكال والهياكل في الكون من حولنا. إن فهم هذه العلاقات وأنواعها وخصائصها يُعد ضروريًا لفهم العديد من المفاهيم الهندسية المتقدمة وله تطبيقات واسعة في شتى المجالات العلمية والعملية والفنية. من خلال إدراك كيف تتشكل الزوايا، وكيف تتوازى وتتعامد المستقيمات، وكيف تتكون الأشكال الهندسية، نتمكن من تحليل العالم وتصميمه والتفاعل معه بأسس رياضية واضحة ومنطقية. إن استيعاب هذه العلاقات يُعزز قدرتنا على التفكير المكاني وحل المشكلات الهندسية وتصور الأبعاد المختلفة، ويُمكننا من تقدير النظام والجمال الكامن في التراكيب الهندسية المحيطة بنا.

تحميل البحث