مقدمة

في عالم الهندسة والرياضيات، غالبًا ما نواجه أشكالًا هندسية أكثر تعقيدًا من الأشكال الأساسية المنتظمة. هذه الأشكال، التي تُعرف بالأشكال المركبة، تتكون من دمج أو تداخل شكلين بسيطين أو أكثر. قد تبدو للوهلة الأولى تحديًا في حساب مساحتها، إلا أن جمال الهندسة يكمن في قدرتنا على تحليل هذه الأشكال المعقدة وتقسيمها إلى مكونات أبسط يمكن التعامل معها بسهولة باستخدام القوانين الهندسية الأساسية. إن فهم مفهوم الأشكال المركبة وكيفية تكوينها، واستيعاب الاستراتيجيات المختلفة لحساب مساحتها سواء بتقسيمها أو بطرح أجزاء منها، يمثل مهارة أساسية في حل المشكلات الهندسية وتطبيق المفاهيم الرياضية في مجالات التصميم والهندسة المعمارية والهندسة الميكانيكية وغيرها من التطبيقات العملية.

لقد نشأت الحاجة إلى حساب مساحات الأشكال المركبة مع تطور التصاميم الهندسية المعقدة، سواء في المباني ذات التخطيطات غير التقليدية أو في الأجزاء الميكانيكية ذات الأبعاد المتداخلة أو حتى في تحليل مناطق جغرافية تتكون من تداخل مساحات مختلفة. وقد أدت هذه الحاجة إلى تطوير استراتيجيات منهجية لتبسيط هذه الأشكال المعقدة وتحويلها إلى مجموعة من المشكلات الهندسية البسيطة التي يمكن حلها باستخدام الأدوات الرياضية الأساسية. إن القدرة على تحليل الأشكال المركبة وحساب مساحتها بدقة تمكن المهندسين والمصممين من تقدير المواد والتكاليف والتخطيط للمشاريع بكفاءة.

مفهوم الأشكال المركبة وكيفية تكوينها

مفهوم الأشكال المركبة: هي أشكال هندسية تتكون من دمج أو تداخل شكلين بسيطين أو أكثر. يمكن أن يكون هذا الدمج أو التداخل بطرق مختلفة، مما ينتج عنه أشكال ذات حدود أكثر تعقيدًا من الأشكال الأساسية. لا يوجد قانون مباشر لحساب مساحة الشكل المركب ككل، بل يتطلب الأمر تحليله إلى مكوناته الأساسية.

كيفية تكوين الأشكال المركبة:

• دمج الأشكال (Addition of Areas): يتكون الشكل المركب عن طريق ضم شكلين بسيطين أو أكثر بحيث يشتركان في جزء من حدودهما أو يتلاصقان تمامًا. في هذه الحالة، تكون مساحة الشكل المركب هي مجموع مساحات الأشكال البسيطة المكونة له (مع الانتباه إلى عدم حساب المساحات المتداخلة مرتين إذا وجدت).
• تداخل الأشكال (Subtraction of Areas): يتكون الشكل المركب عن طريق إزالة جزء أو أكثر من شكل بسيط آخر. في هذه الحالة، تكون مساحة الشكل المركب هي مساحة الشكل الأكبر مطروحًا منها مساحات الأجزاء التي تم إزالتها.

استراتيجيات حساب مساحة الأشكال المركبة

لحساب مساحة شكل مركب، نتبع بشكل أساسي إحدى الاستراتيجيتين التاليتين أو مزيجًا منهما:

استراتيجية التقسيم (Decomposition Strategy):

• تحليل الشكل المركب: يتم فحص الشكل المركب بعناية لتحديد الأشكال البسيطة التي يتكون منها (مثل المربعات، المستطيلات، المثلثات، الدوائر، أنصاف الدوائر، إلخ).
• تقسيم الشكل: يتم تقسيم الشكل المركب إلى هذه الأشكال البسيطة باستخدام خطوط وهمية أو حقيقية. يجب التأكد من أن التقسيم يغطي كامل مساحة الشكل المركب دون تداخل أو ترك فراغات.
• حساب مساحة كل جزء بسيط: يتم حساب مساحة كل شكل بسيط تم الحصول عليه باستخدام القوانين الهندسية المعروفة لمساحة تلك الأشكال.
• جمع المساحات: يتم جمع مساحات جميع الأجزاء البسيطة للحصول على المساحة الكلية للشكل المركب. يجب الانتباه إذا كانت هناك أجزاء متداخلة، حيث يجب حساب مساحتها مرة واحدة فقط أو طرحها إذا تم حسابها ضمن مساحة شكل آخر.

استراتيجية الطرح (Subtraction Strategy):

• تحديد الشكل المحيط: يتم تحديد شكل بسيط أكبر يحيط بالشكل المركب المطلوب حساب مساحته.
• تحديد الأجزاء المزالة: يتم تحديد الأشكال البسيطة التي تم إزالتها من الشكل المحيط لتكوين الشكل المركب المطلوب.
• حساب مساحة الشكل المحيط: يتم حساب مساحة الشكل البسيط الأكبر باستخدام القوانين الهندسية المعروفة.
• حساب مساحات الأجزاء المزالة: يتم حساب مساحة كل شكل بسيط تم إزالته باستخدام القوانين الهندسية المعروفة.
• طرح المساحات: يتم طرح مساحات الأجزاء المزالة من مساحة الشكل المحيط للحصول على مساحة الشكل المركب المطلوب.

أمثلة على تطبيق الاستراتيجيات:

• شكل مركب على شكل حرف “L“: يمكن تقسيمه إلى مستطيلين وجمع مساحتيهما (استراتيجية التقسيم).
• شكل مركب على شكل مربع بداخله دائرة مفرغة: يمكن حساب مساحة المربع ثم طرح مساحة الدائرة (استراتيجية الطرح).
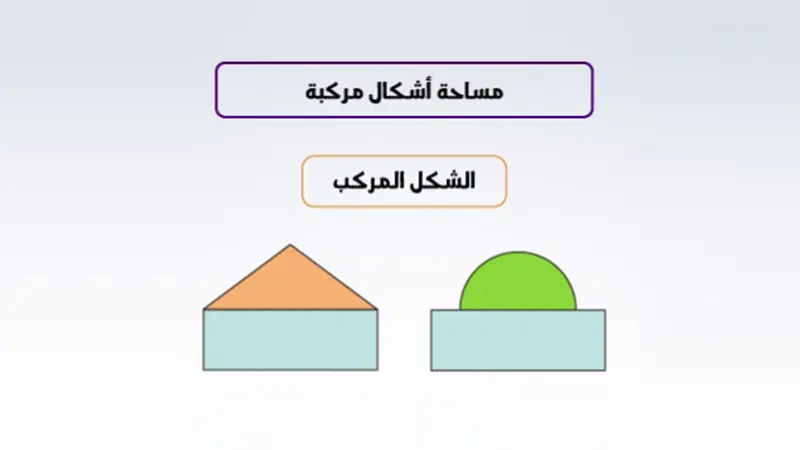
• شكل مركب يتكون من مستطيل يعلوه نصف دائرة: يتم حساب مساحة المستطيل ومساحة نصف الدائرة ثم جمعهما (استراتيجية التقسيم).
• شكل مركب على شكل مستطيل تم اقتطاع مثلث منه: يتم حساب مساحة المستطيل ثم طرح مساحة المثلث (استراتيجية الطرح).

أهمية حساب مساحات الأشكال المركبة وتطبيقاتها العملية

تعتبر القدرة على حساب مساحات الأشكال المركبة مهارة أساسية ذات أهمية كبيرة في العديد من المجالات العملية:

• الهندسة المعمارية والتصميم: حساب مساحة الأرضيات والجدران والأسقف ذات التصميمات غير التقليدية لتقدير مواد البناء والتكاليف. حساب مساحة واجهات المباني ذات الأشكال المعقدة.
• الهندسة المدنية: حساب مساحة الأراضي ذات الحدود غير المستقيمة لتقدير حجم الأعمال الترابية أو لتقسيم الأراضي. حساب مساحة المقاطع العرضية للهياكل المعقدة.
• الهندسة الميكانيكية: حساب مساحة الأسطح المعقدة للأجزاء الميكانيكية لتقدير كمية المواد المطلوبة أو لحساب انتقال الحرارة أو الضغط.
• التصنيع والإنتاج: تقدير مساحة المواد الخام المطلوبة لتصنيع أجزاء ذات أشكال مركبة لتقليل الهدر وتقدير التكاليف.
• تصميم الأزياء والنسيج: حساب مساحة قطع القماش ذات الأشكال المعقدة لتقدير كمية القماش المطلوبة وتخطيط عملية القص.
• الرسم والتصميم الجرافيكي: حساب مساحة الأشكال المركبة في التصاميم لتقدير كمية الطلاء أو الحبر أو لتحديد نسب العناصر المختلفة.
• إدارة الموارد الطبيعية: تقدير مساحة الغابات أو البحيرات أو المناطق الحضرية ذات الحدود غير المنتظمة باستخدام الصور الجوية والفضائية (حيث يتم التعامل مع هذه المناطق كمجموعات من أشكال بسيطة أو أشكال تم اقتطاعها من مناطق أكبر).
• الزراعة: تقدير مساحة الحقول ذات الأشكال غير المنتظمة لتقدير كمية البذور المطلوبة.

الخاتمة

يمثل حساب مساحات الأشكال المركبة تطبيقًا حيويًا للمفاهيم الهندسية الأساسية في التعامل مع تعقيدات الأشكال الواقعية. من خلال استراتيجيات التقسيم الذكي والطرح الدقيق، يمكننا تحويل التحدي إلى فرصة لتطبيق مهارات التحليل الهندسي والوصول إلى حلول عملية. إن هذه القدرة ليست مجرد أداة رياضية، بل هي لغة أساسية للمهندسين والمصممين وصناع القرار في مختلف المجالات، تمكنهم من تحويل الأفكار والتصاميم المعقدة إلى واقع ملموس وفعال. مع استمرار تطور التصاميم الهندسية وتزايد الحاجة إلى تقديرات دقيقة للمساحات في مختلف التطبيقات، ستظل مهارة التعامل مع مساحات الأشكال المركبة ذات أهمية قصوى.