مقدمة

في عالم الهندسة والرياضيات، نتعامل غالبًا مع أشكال هندسية منتظمة ذات قوانين وم formulas محددة لحساب مساحتها، مثل المربعات والمستطيلات والدوائر والمثلثات. إلا أن الواقع من حولنا يعج بالأشكال غير المنتظمة التي لا تتبع هذه القواعد البسيطة، بدءًا من تضاريس الأرض غير المستوية وأشكال الأوراق والأشياء الطبيعية وصولًا إلى التصاميم المعمارية المعقدة والبيانات الإحصائية الممثلة بصور غير قياسية. يمثل قياس مساحة هذه الأشكال تحديًا مثيرًا للاهتمام، حيث لا يمكن تطبيق القوانين الهندسية التقليدية بشكل مباشر. وقد تطورت عبر التاريخ طرق وأساليب رياضية وهندسية متنوعة لتقدير وتقريب مساحات هذه الأشكال بدقة مقبولة، مما فتح آفاقًا واسعة لتطبيقات عملية في مختلف فروع العلوم والهندسة والجغرافيا وغيرها. إن فهم مفهوم الأشكال غير المنتظمة وصعوبة قياس مساحتها بدقة، واستيعاب طرق التقريب المختلفة وأهميتها في مجالات متنوعة، يمثل أساسًا ضروريًا للتعامل مع العالم الحقيقي الذي يندر فيه وجود الكمال الهندسي.

لقد واجه المهندسون والعلماء على مر العصور الحاجة إلى قياس مساحات الأراضي ذات الحدود المتعرجة، أو تقدير مساحة أسطح ذات انحناءات غير منتظمة، أو تحليل بيانات ممثلة بأشكال لا تخضع لقواعد رياضية بسيطة. وقد أدت هذه الحاجة إلى تطوير أدوات وتقنيات مبتكرة، بدءًا من الطرق اليدوية البسيطة وصولًا إلى الخوارزميات الحاسوبية المعقدة وتقنيات الاستشعار عن بعد. إن القدرة على تقدير مساحات الأشكال غير المنتظمة بدقة معقولة أصبحت أداة لا غنى عنها في مجالات مثل رسم الخرائط، وإدارة الموارد الطبيعية، وتحليل الصور الطبية، وتصميم الأجزاء الهندسية المعقدة.

مفهوم الأشكال غير المنتظمة وصعوبة قياس مساحتها بدقة

مفهوم الأشكال غير المنتظمة: هي الأشكال الهندسية التي لا تتبع تعريفات محددة للأشكال المنتظمة مثل المربعات والمستطيلات والدوائر والمثلثات ذات الأبعاد والزوايا الثابتة. تتميز هذه الأشكال بحدود منحنية أو متعرجة أو بأبعاد وزوايا متغيرة بشكل غير قياسي، مما يجعل من الصعب وصفها بمعادلات رياضية بسيطة أو تطبيق قوانين هندسية مباشرة لحساب مساحتها.

صعوبة قياس مساحتها بدقة: تكمن صعوبة قياس مساحة الأشكال غير المنتظمة في عدم وجود قوانين هندسية جاهزة يمكن تطبيقها مباشرة. فالمساحة تُحسب عادةً بضرب الأبعاد الخطية (مثل الطول والعرض أو نصف القطر تربيع في باي)، وهذه الأبعاد غير ثابتة أو غير معرفة بوضوح في الأشكال غير المنتظمة. على سبيل المثال، لا يمكن تحديد “طول” أو “عرض” محددين لشكل ورقة شجرة ذات حواف متعرجة. وبالمثل، فإن الأسطح ذات الانحناءات غير المنتظمة لا يمكن وصفها بنصف قطر ثابت لتطبيق قانون مساحة الدائرة أو الكرة. هذه الصعوبة تجعل من الحصول على قيمة دقيقة لمساحة الشكل غير المنتظم أمرًا بالغ الصعوبة أو حتى مستحيلاً باستخدام الأدوات الهندسية الأساسية.

طرق تقريب مساحات الأشكال غير المنتظمة

نظرًا لصعوبة القياس الدقيق، تم تطوير العديد من الطرق لتقريب مساحات الأشكال غير المنتظمة بدقة مقبولة للتطبيقات العملية:

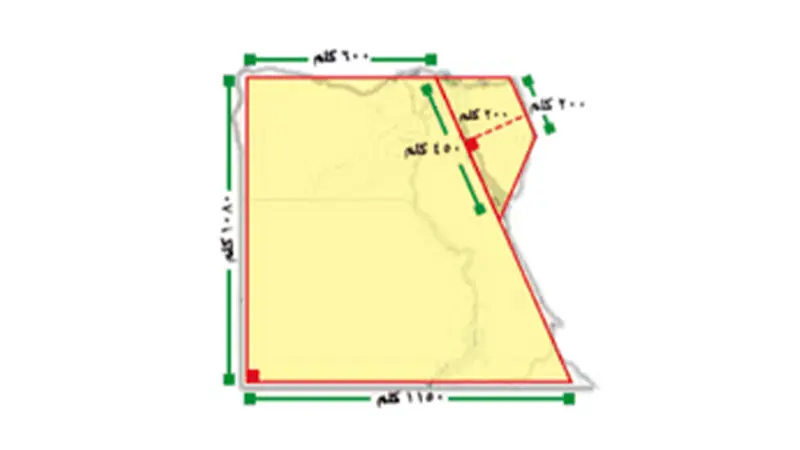
1. طريقة التقطيع والتحويل (Triangulation and Decomposition): تعتمد هذه الطريقة على تقسيم الشكل غير المنتظم إلى عدد من الأشكال المنتظمة الأصغر التي يمكن حساب مساحتها بسهولة، مثل المثلثات أو المستطيلات أو الأشباه منحرفات. ثم يتم جمع مساحات هذه الأجزاء لتقدير المساحة الكلية للشكل غير المنتظم. كلما زاد عدد الأجزاء المنتظمة المستخدمة في التقسيم، زادت دقة التقريب.
2. طريقة التربيع (Grid Method): يتم وضع شبكة من المربعات ذات الأبعاد المعروفة فوق الشكل غير المنتظم. ثم يتم عد المربعات الكاملة التي تقع داخل حدود الشكل، وتقدير مساحة الأجزاء غير الكاملة من المربعات الواقعة على الحدود (عادةً بتقدير بصري أو باعتبار المربعات التي يغطيها الشكل بأكثر من نصفها مربعات كاملة). يتم ضرب عدد المربعات (الكاملة والمقدرة) في مساحة المربع الواحد للحصول على تقدير لمساحة الشكل غير المنتظم. دقة هذه الطريقة تعتمد على حجم المربعات في الشبكة؛ كلما كانت المربعات أصغر، زادت دقة التقريب.
3. طريقة متوسط الإحداثيات (Shoelace Formula أو Surveyor’s Formula): تستخدم هذه الطريقة إذا كانت إحداثيات رؤوس الشكل غير المنتظم معروفة في نظام إحداثيات ثنائي الأبعاد. تعتمد على عملية حسابية بسيطة تتضمن ضرب وتبديل إحداثيات الرؤوس بترتيب معين ثم أخذ نصف القيمة المطلقة للنتيجة. توفر هذه الطريقة قيمة دقيقة لمساحة أي مضلع بسيط (سواء كان منتظمًا أو غير منتظم) إذا كانت إحداثيات رؤوسه معروفة بدقة.
4. طرق التكامل العددي (Numerical Integration): إذا كان بالإمكان وصف حدود الشكل غير المنتظم بدوال رياضية (حتى لو كانت معقدة)، يمكن استخدام طرق التكامل العددي لتقدير المساحة الواقعة تحت المنحنى أو بين المنحنيات التي تحدد الشكل. تشمل هذه الطرق قاعدة شبه المنحرف (Trapezoidal Rule)، وقاعدة سيمبسون (Simpson’s Rule)، وغيرها من الطرق التي تقسم المنطقة إلى شرائح صغيرة وتقدر مساحة كل شريحة ثم تجمعها.
5. طريقة المسح بالبلانيمتر (Planimeter): البلانيمتر هو أداة ميكانيكية تستخدم لتحديد مساحة شكل مستوٍ غير منتظم عن طريق تتبع محيطه بقلم خاص. تقوم الآلية الداخلية للأداة بحساب المساحة المحصورة بناءً على حركة القلم.
6. الطرق الرقمية (Digital Methods): في العصر الرقمي، يتم استخدام برامج الحاسوب وتقنيات معالجة الصور لتقدير مساحات الأشكال غير المنتظمة. على سبيل المثال، في تحليل الصور الرقمية، يمكن عد عدد البكسلات التي تشكل الشكل غير المنتظم، وإذا كانت دقة الصورة معروفة (حجم البكسل الفعلي)، يمكن تقدير المساحة بضرب عدد البكسلات في مساحة البكسل الواحد.
7. تقنيات الاستشعار عن بعد (Remote Sensing): تستخدم الصور الجوية والفضائية وبيانات الاستشعار عن بعد لتقدير مساحات الأراضي والغابات والمسطحات المائية ذات الحدود غير المنتظمة. تعتمد هذه التقنيات على تحليل بيانات البكسلات وتصنيفها لتحديد المساحات المطلوبة.

أهمية طرق تقريب المساحات وتطبيقاتها الواسعة

تكتسب طرق تقريب مساحات الأشكال غير المنتظمة أهمية بالغة نظرًا لتطبيقاتها الواسعة في مختلف فروع العلوم والهندسة وغيرها:

• رسم الخرائط والجغرافيا: تقدير مساحات الدول والمحافظات والبحيرات والغابات والأراضي الزراعية ذات الحدود الطبيعية غير المنتظمة باستخدام الصور الجوية والفضائية وتقنيات الاستشعار عن بعد.
• إدارة الموارد الطبيعية: قياس مساحة الغطاء النباتي، وتقدير مساحة المناطق المتضررة من الحرائق أو الفيضانات، وحساب مساحة المسطحات المائية المتغيرة.
• الطب الحيوي وتحليل الصور الطبية: تقدير مساحة الأورام أو الآفات الجلدية في الصور الطبية لتتبع نموها أو استجابتها للعلاج. تحليل صور الخلايا والأنسجة تحت المجهر.
• الهندسة المعمارية والتصميم: حساب مساحة الأسطح ذات التصاميم غير التقليدية أو المنحنية لتقدير تكاليف المواد أو الطاقة.
• الهندسة المدنية: تقدير مساحة الأراضي ذات التضاريس غير المستوية لحساب كميات الحفر والردم أو لتقدير تكاليف المشاريع الإنشائية.
• علوم البيئة: تقدير مساحة المناطق المتأثرة بالتلوث أو التصحر، ومراقبة التغيرات في الغطاء الأرضي.
• تحليل الصور الرقمية ومعالجة الفيديو: قياس مساحة الأجسام غير المنتظمة في الصور ومقاطع الفيديو لتطبيقات مثل التعرف على الأنماط وتتبع الحركة.
• الفيزياء وعلوم المواد: تقدير مساحة الأسطح غير المنتظمة للمواد النانوية أو الأغشية الرقيقة لدراسة خواصها.
• الرياضيات التطبيقية والنمذجة: استخدام التكامل العددي لتقدير المساحات تحت المنحنيات التي تمثل ظواهر طبيعية أو نماذج رياضية معقدة.

الخاتمة

على الرغم من التحديات التي تفرضها الأشكال غير المنتظمة في قياس مساحتها بدقة، فقد تطورت عبر التاريخ طرق وأساليب رياضية وهندسية مبتكرة لتقدير هذه المساحات بدقة مقبولة. بدءًا من الطرق الهندسية البسيطة وصولًا إلى التقنيات الرقمية المتقدمة، أصبحت القدرة على تقريب مساحات هذه الأشكال أداة لا غنى عنها في العديد من المجالات العلمية والهندسية والتطبيقية. إن فهم هذه الطرق وتقدير أهميتها يسلط الضوء على مرونة الرياضيات وقدرتها على التعامل مع تعقيدات العالم الحقيقي، ويؤكد على الدور الحيوي للتقريب في حل المشكلات العملية التي لا يمكن حلها بالطرق التحليلية الدقيقة وحدها. مع استمرار التطور التكنولوجي، من المتوقع ظهور طرق أكثر دقة وكفاءة لتقدير مساحات الأشكال غير المنتظمة، مما سيفتح آفاقًا جديدة للتطبيقات في المستقبل.