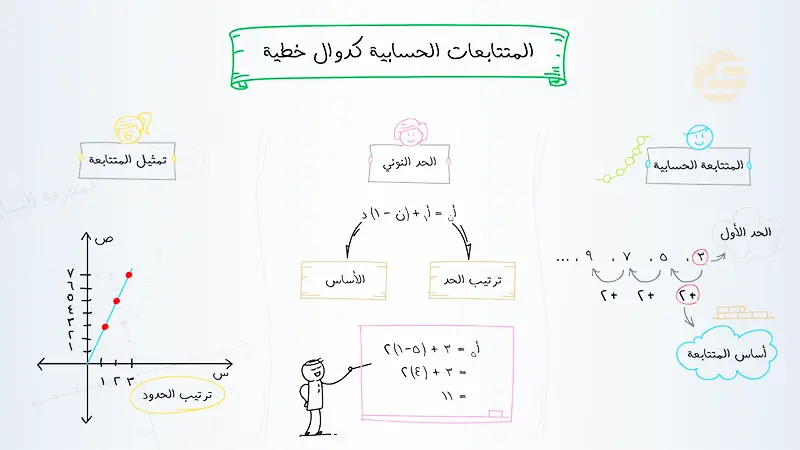
مقدمة

في عالم الرياضيات الشيق، تُعد المتتابعات الحسابية (Arithmetic Sequences) من المفاهيم الأساسية التي تُعنى بدراسة الأنماط العددية المنظمة. تتميز المتتابعة الحسابية بأن الفرق بين أي حدين متتاليين فيها ثابت، ويُعرف هذا الفرق بـ الأساس المشترك (Common Difference). للوهلة الأولى، قد تبدو المتتابعات الحسابية مجرد سلاسل من الأرقام، ولكن عند التعمق في خصائصها، نكتشف علاقة جوهرية تُربطها بمفهوم رياضي آخر لا يقل أهمية وهو الدوال الخطية (Linear Functions). إن فهم أن المتتابعة الحسابية هي في جوهرها دالة خطية يُمكننا من تطبيق أدوات الجبر والتمثيل البياني لفهم سلوك هذه المتتابعات بشكل أعمق. هذا الربط بين الأنماط العددية والجبر يُسهم في تعزيز الفهم الرياضي الشامل، ويفتح آفاقًا جديدة لحل المشكلات في مختلف المجالات، من العلوم والاقتصاد إلى الحوسبة والحياة اليومية.

مفهوم المتتابعة الحسابية وخصائصها

تعريف المتتابعة الحسابية: المتتابعة الحسابية هي قائمة من الأعداد يُحصل فيها على كل حد (بعد الحد الأول) بإضافة قيمة ثابتة إلى الحد الذي يسبقه. هذه القيمة الثابتة تُسمى الأساس المشترك (Common Difference)، ويُرمز لها عادةً بالرمز d.

أمثلة على المتتابعات الحسابية:

• 3, 6, 9, 12, 15, … (الأساس المشترك d=3)
• 10, 8, 6, 4, 2, … (الأساس المشترك d=−2)
• 5, 5, 5, 5, 5, … (الأساس المشترك d=0)

الحد العام للمتتابعة الحسابية: يُمكن إيجاد أي حد في المتتابعة الحسابية باستخدام صيغة الحد العام. إذا كان a1​ هو الحد الأول، و d هو الأساس المشترك، و n هو رقم الحد (ترتيبه في المتتابعة)، فإن الحد an​ يُعطى بالصيغة: an​=a1​+(n−1)d هذه الصيغة حيوية لأنها تسمح لنا بحساب أي حد في المتتابعة دون الحاجة لسرد جميع الحدود السابقة.

مفهوم الدالة الخطية وخصائصها

تعريف الدالة الخطية: الدالة الخطية هي دالة يمكن تمثيلها بيانياً بخط مستقيم. تُصف هذه الدوال علاقة يتغير فيها المتغير التابع بمعدل ثابت بالنسبة للمتغير المستقل.

الشكل العام للدالة الخطية: يُمكن التعبير عن الدالة الخطية عادةً بالصيغة: y=mx+b حيث:

• y: هو المتغير التابع (المخرج).
• x: هو المتغير المستقل (المدخل).
• m: هو الميل (Slope)، ويُمثل معدل التغير الثابت للدالة.
• b: هو الجزء المقطوع من المحور الصادي (y-intercept)، وهي قيمة y عندما تكون x تساوي صفرًا.

العلاقة بين الميل ومعدل التغير: كما ذكرنا سابقًا، الميل في الدالة الخطية هو نفسه معدل التغير الثابت. إنه يحدد مدى انحدار الخط واتجاهه. إذا كان الميل موجبًا، فإن الخط يتجه للأعلى. إذا كان سالبًا، يتجه للأسفل. إذا كان صفرًا، يكون الخط أفقيًا.

لماذا تُعد المتتابعات الحسابية دوالًا خطية

يكمن جوهر العلاقة بين المتتابعات الحسابية والدوال الخطية في مفهوم التغير الثابت.

• التغير الثابت في المتتابعات الحسابية: في المتتابعة الحسابية، يُمثل الأساس المشترك (d) مقدار التغير الثابت بين كل حد والحد الذي يليه. كلما زاد رقم الحد (n) بمقدار 1، يزداد (أو ينقص) قيمة الحد (an​) بمقدار d. هذا هو بالضبط ما يعنيه معدل التغير الثابت.
• الربط بالدالة الخطية: لنتأمل صيغة الحد العام للمتتابعة الحسابية مرة أخرى: an​=a1​+(n−1)d يمكننا إعادة ترتيب هذه المعادلة لتُشبه صيغة الدالة الخطية y=mx+b: an​=dn+(a1​−d) بمقارنة هذه الصيغة بالصيغة y=mx+b:
  • المتغير التابع (y) هو an​ (قيمة الحد).
  • المتغير المستقل (x) هو n (رقم الحد).
  • الميل (m) هو d (الأساس المشترك). وهذا يُظهر بوضوح أن الأساس المشترك للمتتابعة الحسابية هو معدل التغير الثابت، وهو ما يُمثل الميل.
  • الجزء المقطوع من المحور الصادي (b) هو (a1​−d). يُمثل هذا قيمة “الحد الصفري” النظري، أي قيمة الحد إذا كان ترتيبه صفرًا.
• التمثيل البياني: عندما نمثل نقاط المتتابعة الحسابية بيانياً على مستوى الإحداثيات، حيث يُمثل المحور الأفقي رقم الحد (n) والمحور الرأسي قيمة الحد (an​)، فإن هذه النقاط تقع على خط مستقيم. هذا الخط المستقيم هو التمثيل البياني للدالة الخطية التي تُمثل المتتابعة الحسابية.

تمثيل المتتابعات الحسابية بيانياً

لتمثيل متتابعة حسابية بيانياً، نتبع الخطوات التالية:

1. تحديد الأزواج المرتبة: كل حد في المتتابعة يشكل زوجًا مرتبًا (n,an​)، حيث n هو ترتيب الحد و an​ هو قيمة الحد.
   • الحد الأول: (1,a1​)
   • الحد الثاني: (2,a2​)
   • الحد الثالث: (3,a3​) وهكذا.
2. رسم النقاط: نحدد هذه الأزواج المرتبة كنقاط على مستوى الإحداثيات.
3. توصيل النقاط (اختياري، ولكن توضيحي): يمكن توصيل النقاط بخط مستقيم، مع العلم أن المتتابعات الحسابية هي دوال منفصلة (Discrete Functions)، أي أن القيم موجودة فقط عند الأعداد الصحيحة لـ n. ومع ذلك، رسم الخط يساعد على رؤية العلاقة الخطية.

مثال: مثل المتتابعة الحسابية 3, 6, 9, 12, … بيانياً.

• الحد الأول: a1​=3
• الأساس المشترك: d=3
• الأزواج المرتبة:
  • (1,3)
  • (2,6)
  • (3,9)
  • (4,12)
• عند رسم هذه النقاط، ستلاحظ أنها تقع على خط مستقيم. الميل لهذا الخط سيكون 3، وهو الأساس المشترك للمتتابعة.

تطبيقات فهم المتتابعات الحسابية كدوال خطية

فهم هذا الربط يُمكننا من حل مشكلات متنوعة ويُسهم في مجالات متعددة:

1. التنبؤ بقيم مستقبلية: باستخدام صيغة الدالة الخطية (الحد العام)، يمكننا التنبؤ بقيمة أي حد مستقبلي في المتتابعة الحسابية دون الحاجة لحساب جميع الحدود السابقة.
   • مثال: إذا كان راتب موظف يزيد بمبلغ ثابت كل عام، يمكننا استخدام المتتابعة الحسابية كدالة خطية لتوقع راتبه في أي عام مستقبلي.
2. تحليل البيانات والأنماط: يُمكننا هذا الفهم من تحديد ما إذا كانت مجموعة من البيانات تتبع نمطًا خطيًا أم لا، وإيجاد القاعدة التي تصف هذا النمط.
   • مثال: تحليل معدلات النمو السكاني، أو تغير درجات الحرارة عبر فترات زمنية ثابتة.
3. حل مشكلات مالية: في حسابات الفائدة البسيطة، حيث يزداد المبلغ بمقدار ثابت كل فترة زمنية، يمكن نمذجة ذلك باستخدام المتتابعات الحسابية كدوال خطية.
4. علم الحاسوب: في برمجة بعض الخوارزميات التي تتطلب توليد سلاسل عددية بنمط ثابت.
5. الفيزياء: وصف الحركة المنتظمة، حيث تكون السرعة ثابتة، ويُمثل التغير في المسافة بالنسبة للزمن دالة خطية.

الخاتمة

إن الربط بين المتتابعات الحسابية والدوال الخطية ليس مجرد تقارب رياضي، بل هو نافذة تطل على فهم أعمق للأنماط العددية وكيفية تجسدها في العلاقات الخطية. إن إدراك أن الأساس المشترك للمتتابعة الحسابية هو الميل في الدالة الخطية المقابلة يُسهم في توحيد المفاهيم الجبرية والبيانية، ويُعزز القدرة على التحليل والتنبؤ. من خلال تحويل هذه الأنماط العددية إلى تمثيلات بيانية على خطوط مستقيمة، نكتسب أداة قوية لحل المشكلات في مجالات متنوعة، من العلوم والهندسة إلى الاقتصاد والحياة اليومية. هذا الفهم يُشكل أساسًا متينًا لمزيد من الاستكشاف في عالم الدوال وأنماطها، ويُمكن المتعلم من رؤية الجمال والترابط في بنية الرياضيات.