توسع المتوسط والوسيط والمنوال
مقدمة
لطالما شكلت مقاييس النزعة المركزية الثلاثة الأساسية – المتوسط الحسابي، والوسيط، والمنوال – حجر الزاوية في الإحصاء الوصفي، حيث تُقدم ملخصات موجزة حول القيمة “النموذجية” لمجموعة من البيانات. بيد أن فهم هذه المقاييس لا يتوقف عند طرق حسابها الأولية وتطبيقاتها البسيطة. هناك “توسع” في مفاهيمها وتطبيقاتها يتجاوز الأساسيات، يشمل استكشاف أنواع مختلفة من المتوسطات، وفهم أعمق لخصائص الوسيط في التوزيعات المعقدة، وتطبيقات متقدمة للمنوال في مجالات متنوعة. هذا التوسع يكشف عن ثراء هذه المقاييس وقدرتها على تقديم رؤى أعمق حول طبيعة البيانات وتوزيعها في سياقات إحصائية أكثر تعقيدًا.
إن “توسع المتوسط” يعني الخروج من نطاق المتوسط الحسابي البسيط إلى استكشاف أنواع أخرى من المتوسطات التي تكون أكثر ملاءمة لأنواع معينة من البيانات أو أغراض تحليلية محددة. يشمل ذلك المتوسط الهندسي الذي يُستخدم بشكل خاص للبيانات التي تنمو بشكل مضاعف أو لحساب متوسط النسب، والمتوسط التوافقي الذي يُستخدم لحساب متوسط المعدلات. كما يتضمن فهم كيفية تأثير الأوزان المختلفة على حساب المتوسط الموزون، والذي يُستخدم عندما تكون بعض القيم في البيانات أكثر أهمية من غيرها. أما “توسع الوسيط” فيتجاوز إيجاد القيمة الوسطى في البيانات المرتبة ليشمل فهم سلوكه في التوزيعات الاحتمالية المختلفة، واستخدامه في الإحصاءات اللا معلمية حيث لا تُفترض توزيعات محددة للبيانات، وتطبيقاته في تحليل البيانات الضخمة. وبالمثل، فإن “توسع المنوال” لا يقتصر على تحديد القيمة الأكثر تكرارًا، بل يشمل تحليل التوزيعات متعددة المنوالات وتفسيرها، واستخدامه في تحديد الأنماط السائدة في البيانات النوعية والكمية المنفصلة، وتطبيقاته في مجالات مثل تحليل سلوك المستهلك وعلم الأحياء.
توسع المتوسط (Beyond the Arithmetic Mean)
بينما يُعد المتوسط الحسابي هو الأكثر شيوعًا، هناك أنواع أخرى من المتوسطات تُستخدم في سياقات محددة:
- المتوسط الهندسي (Geometric Mean): يُستخدم لحساب متوسط النسب أو المعدلات، أو للبيانات التي تنمو بشكل مضاعف (مثل النمو السكاني أو العائد على الاستثمار المركب). يتم حسابه بأخذ الجذر النوني لحاصل ضرب n قيمة.
- المتوسط التوافقي (Harmonic Mean): يُستخدم لحساب متوسط المعدلات عندما تكون الوحدات مختلفة (مثل متوسط السرعات عندما تكون المسافات متساوية). يتم حسابه بأخذ مقلوب متوسط مقلوبات القيم.
- المتوسط الموزون (Weighted Mean): يُستخدم عندما تكون بعض القيم في البيانات أكثر أهمية من غيرها، حيث يتم إعطاء كل قيمة وزنًا مختلفًا قبل حساب المتوسط الحسابي.
فهم هذه الأنواع المختلفة من المتوسطات يسمح بتحليل البيانات بشكل أكثر دقة وملاءمة لطبيعتها.
توسع الوسيط
يتجاوز فهم الوسيط مجرد إيجاد القيمة الوسطى. خصائصه تجعله مفيدًا في حالات معينة:
- مقاومة القيم المتطرفة: كما ذكرنا، الوسيط أقل حساسية للقيم المتطرفة مقارنة بالمتوسط الحسابي، مما يجعله مقياسًا أفضل للنزعة المركزية في البيانات الملتوية أو التي تحتوي على قيم شاذة.
- الإحصاءات اللا معلمية: يُستخدم الوسيط بشكل واسع في الإحصاءات اللا معلمية، وهي أساليب إحصائية لا تفترض توزيعًا احتماليًا محددًا للبيانات.
- البيانات الترتيبية: يمكن استخدام الوسيط للبيانات الترتيبية (مثل تقييمات العملاء على مقياس من 1 إلى 5) حيث لا يكون للمسافات بين القيم معنى كمي دقيق.
- تحليل البيانات الضخمة: في مجموعات البيانات الكبيرة جدًا، قد يكون حساب الوسيط أكثر كفاءة من حساب المتوسط الحسابي من الناحية الحاسوبية في بعض الحالات.
توسع المنوال
لا يقتصر فهم المنوال على تحديد القيمة الأكثر تكرارًا:
- التوزيعات متعددة المنوالات: وجود أكثر من منوال في البيانات يشير إلى وجود مجموعات فرعية متميزة داخل البيانات. تحليل هذه المنوالات يمكن أن يكشف عن أنماط مهمة. على سبيل المثال، في تحليل أعمار العملاء في متجر، قد يشير وجود منوالين إلى وجود شريحتين رئيسيتين من العملاء.
- البيانات النوعية: المنوال هو المقياس الرئيسي للنزعة المركزية للبيانات النوعية (مثل تحديد اللون الأكثر شيوعًا للسيارات في مدينة ما).
- تطبيقات في مجالات متنوعة:
- تحليل سلوك المستهلك: تحديد المنتج الأكثر مبيعًا أو المفضل.
- علم الأحياء: تحديد الفئة الأكثر شيوعًا في تصنيف الكائنات الحية.
- تحليل النصوص: تحديد الكلمة الأكثر تكرارًا في نص ما.
- التعليم: تحديد درجة النجاح الأكثر شيوعًا بين الطلاب.
العلاقة بين المتوسط والوسيط والمنوال وشكل التوزيع
يعطي موقع المتوسط والوسيط والمنوال بالنسبة لبعضهم البعض فكرة عن شكل توزيع البيانات:
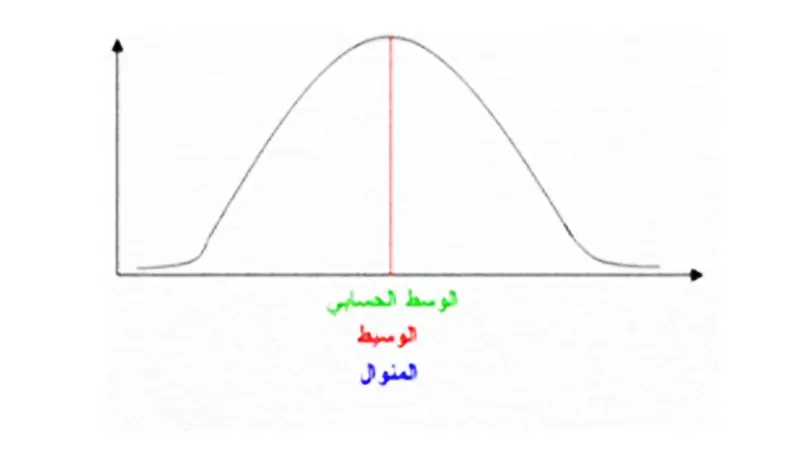
- التوزيع المتماثل: في التوزيع المتماثل (مثل التوزيع الطبيعي)، يكون المتوسط والوسيط والمنوال متساويين أو متقاربين جدًا.
- التوزيع الملتوي لليمين: في التوزيع الملتوي لليمين، يكون المنوال أصغر من الوسيط، الذي يكون أصغر من المتوسط (المنوال < الوسيط < المتوسط).
- التوزيع الملتوي لليسار: في التوزيع الملتوي لليسار، يكون المتوسط أصغر من الوسيط، الذي يكون أصغر من المنوال (المتوسط < الوسيط < المنوال).
فهم هذه العلاقة يساعد في تفسير طبيعة البيانات وتوزيعها.
استخدامات متقدمة لمقاييس النزعة المركزية
تُستخدم مقاييس النزعة المركزية في العديد من التحليلات الإحصائية المتقدمة ونماذج التنبؤ. على سبيل المثال، المتوسط الحسابي هو أساس العديد من الاختبارات الإحصائية (مثل اختبار t واختبار ANOVA). كما أن فهم القيمة النموذجية للبيانات يُستخدم في بناء نماذج التنبؤ وتحليل الانحدار. اختيار المقياس المناسب للنزعة المركزية يمكن أن يؤثر بشكل كبير على نتائج هذه التحليلات.
تحديات ومفاهيم خاطئة حول مقاييس النزعة المركزية
من المهم إدراك بعض التحديات والمفاهيم الخاطئة المتعلقة بمقاييس النزعة المركزية:
- افتراض “النموذجية”: قد يُفترض خطأً أن مقياس النزعة المركزية يمثل “القيمة النموذجية” لجميع البيانات، بينما قد لا يكون هذا صحيحًا في التوزيعات المتعددة القمم أو شديدة التباين.
- تأثير القيم المتطرفة: يجب أن يكون المستخدم واعيًا لتأثير القيم المتطرفة على المتوسط الحسابي واختيار المقياس المناسب بناءً على ذلك.
- تفسير المنوال: في التوزيعات التي تحتوي على عدة منوالات، يجب تفسير كل منوال في سياق البيانات.
الخاتمة
إن توسع فهمنا لمقاييس النزعة المركزية – المتوسط والوسيط والمنوال – يتجاوز طرق حسابها الأولية ليكشف عن أدوات تحليلية قوية ومتعددة الاستخدامات. من خلال استكشاف أنواع مختلفة من المتوسطات، وفهم خصائص الوسيط في التوزيعات المعقدة، وتحليل التطبيقات المتقدمة للمنوال، نكتسب رؤى أعمق حول طبيعة البيانات وتوزيعها. اختيار المقياس المناسب للنزعة المركزية بناءً على طبيعة البيانات وسؤال البحث المطروح هو مفتاح استخلاص معلومات دقيقة وذات مغزى. إن هذا التوسع في فهم هذه المقاييس الأساسية يُعزز قدرتنا على تحليل البيانات بشكل أكثر شمولية واتخاذ قرارات أكثر استنارة في مختلف المجالات.


