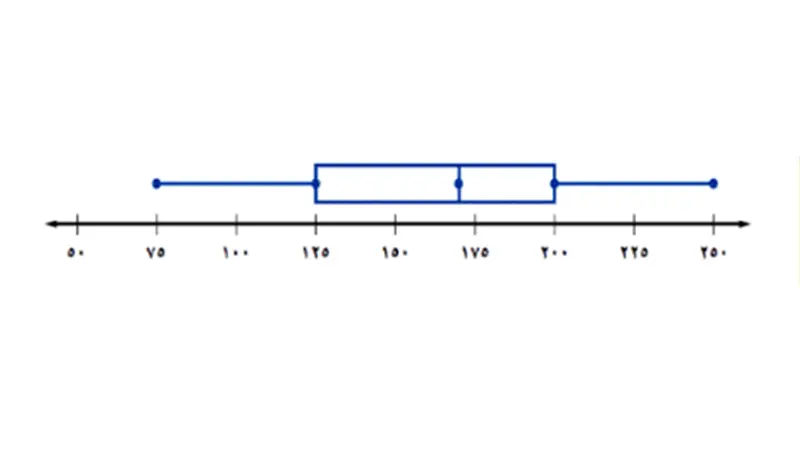
مقدمة

في رحلة استكشاف البيانات وتحليلها، نحتاج إلى أدوات بصرية تُمكننا من تلخيص المعلومات المعقدة وتقديمها بطريقة سهلة الفهم. يُعد التمثيل بالصندوق وطرفيه (Box and Whisker Plot أو Box Plot) أحد هذه الأدوات القوية والفعالة، حيث يُقدم ملخصًا بصريًا شاملاً لتوزيع مجموعة من البيانات الكمية. لا يقتصر هذا التمثيل على إظهار مقاييس النزعة المركزية فحسب، بل يُبرز أيضًا مقاييس التشتت والشكل العام لتوزيع البيانات، بالإضافة إلى تحديد القيم المتطرفة المحتملة. بفضل بساطته وقدرته على تلخيص خمس قيم إحصائية هامة (الحد الأدنى، الربع الأول، الوسيط، الربع الثالث، والحد الأقصى)، يُستخدم التمثيل بالصندوق وطرفيه على نطاق واسع في مختلف المجالات لمقارنة توزيعات مجموعات بيانات مختلفة، وتحديد مدى تماثل البيانات أو التوائها، والكشف عن القيم غير الاعتيادية. إن فهم كيفية إنشاء هذا التمثيل البياني وتفسيره يُعد مهارة أساسية في التحليل الإحصائي الوصفي.

لم يقتصر دور التمثيل بالصندوق وطرفيه على مجرد تلخيص البيانات وعرضها بصريًا، بل امتد ليشمل استخدامه كأداة استكشافية أولية لفهم الخصائص الرئيسية لتوزيع البيانات قبل تطبيق المزيد من التحليلات الإحصائية المتقدمة. فهو يُمكن المحلل من الحصول على نظرة عامة سريعة على مدى تمركز البيانات، ومدى انتشارها، وشكل توزيعها (هل هو متماثل، ملتوي لليمين، ملتوي لليسار؟)، ووجود أي قيم متطرفة قد تستدعي المزيد من التحقيق. كما أن التمثيل بالصندوق وطرفيه يُعد أداة ممتازة لمقارنة توزيعات متغير واحد عبر مجموعات مختلفة، مما يُسهل عملية تحديد الاختلافات والتشابهات بين هذه المجموعات. إن القدرة على قراءة هذا التمثيل البياني وتفسيره بشكل صحيح تُمكّننا من استخلاص رؤى قيمة من البيانات واتخاذ قرارات أكثر استنارة.

تعريف التمثيل بالصندوق وطرفيه

التمثيل بالصندوق وطرفيه هو رسم بياني يلخص توزيع مجموعة من البيانات الكمية باستخدام خمس قيم إحصائية أساسية:

1. الحد الأدنى (Minimum): أصغر قيمة في مجموعة البيانات.
2. الربع الأول (Q1 أو 25th Percentile): القيمة التي يقع تحتها 25% من البيانات بعد ترتيبها.
3. الوسيط (Median أو Q2 أو 50th Percentile): القيمة التي يقع تحتها 50% من البيانات (القيمة الوسطى).
4. الربع الثالث (Q3 أو 75th Percentile): القيمة التي يقع تحتها 75% من البيانات بعد ترتيبها.
5. الحد الأقصى (Maximum): أكبر قيمة في مجموعة البيانات.

خطوات إنشاء التمثيل بالصندوق وطرفيه

1. ترتيب البيانات: ترتيب مجموعة البيانات من الأصغر إلى الأكبر.
2. حساب القيم الخمس الملخصة: تحديد الحد الأدنى، والربع الأول، والوسيط، والربع الثالث، والحد الأقصى للبيانات.
3. رسم الصندوق: رسم مستطيل (الصندوق) يمتد من الربع الأول (Q1) إلى الربع الثالث (Q3).
4. رسم خط الوسيط: رسم خط أفقي داخل الصندوق يمثل قيمة الوسيط.
5. حساب المدى الربيعي الداخلي (IQR): IQR = Q3 – Q1.
6. تحديد الحدود العليا والسفلى للأطراف (Whiskers): تُستخدم هذه الحدود لتحديد القيم “النموذجية” القصوى والدنيا. عادة ما تُحسب الحدود على النحو التالي:
   • الحد العلوي = Q3 + 1.5 * IQR
   • الحد السفلي = Q1 – 1.5 * IQR
7. رسم الأطراف (Whiskers): رسم خطين أفقيين (الأطراف) يمتدان من منتصف ضلعي الصندوق إلى أبعد قيمة في البيانات تقع ضمن الحدود العليا والسفلى المحسوبة.
8. تحديد القيم المتطرفة: أي قيم تقع خارج الأطراف (أعلى الحد العلوي أو أقل من الحد السفلي) تُعتبر قيمًا متطرفة ويتم تمثيلها بنقاط فردية أو رموز أخرى.

العناصر الأساسية للتمثيل بالصندوق وطرفيه

يتكون التمثيل بالصندوق وطرفيه من العناصر التالية:

• الصندوق (Box): يمثل النطاق الذي تقع فيه الـ 50% الوسطى من البيانات (من الربع الأول إلى الربع الثالث). طول الصندوق يمثل المدى الربيعي الداخلي (IQR).
• خط الوسيط (Median Line): خط داخل الصندوق يشير إلى قيمة الوسيط.
• الأطراف (Whiskers): خطوط تمتد من الصندوق إلى القيم القصوى والدنيا ضمن الحدود المحددة. تعطي فكرة عن مدى انتشار الجزء العلوي والسفلي من البيانات.
• القيم المتطرفة (Outliers): نقاط فردية تقع خارج الأطراف، وتشير إلى قيم غير اعتيادية قد تحتاج إلى مزيد من التحقيق.

استخدام التمثيل بالصندوق وطرفيه في تلخيص البيانات وتحديد خصائص توزيعها

يُعد التمثيل بالصندوق وطرفيه أداة قوية لتلخيص البيانات وتحديد خصائص توزيعها بشكل بصري:

• النزعة المركزية: يمكن تحديد موقع الوسيط داخل الصندوق لتقدير مركز التوزيع.
• التشتت: طول الصندوق (IQR) يشير إلى تشتت الـ 50% الوسطى من البيانات. طول الأطراف يعطي فكرة عن تشتت بقية البيانات ضمن الحدود الطبيعية.
• شكل التوزيع:
  • التوزيع المتماثل: يكون الوسيط في منتصف الصندوق تقريبًا، ويكون طول الطرفين متساويًا تقريبًا، ولا توجد العديد من القيم المتطرفة.
  • التوزيع الملتوي لليمين: يكون الوسيط أقرب إلى الربع الأول، ويكون الطرف الأيمن أطول من الطرف الأيسر، وقد توجد قيم متطرفة على الجانب الأيمن.
  • التوزيع الملتوي لليسار: يكون الوسيط أقرب إلى الربع الثالث، ويكون الطرف الأيسر أطول من الطرف الأيمن، وقد توجد قيم متطرفة على الجانب الأيسر.
• القيم المتطرفة: النقاط المنفصلة خارج الأطراف تُشير إلى قيم قد تكون غير اعتيادية أو ناتجة عن أخطاء في جمع البيانات.

التطبيقات العملية للتمثيل بالصندوق وطرفيه في مجالات متنوعة

يُستخدم التمثيل بالصندوق وطرفيه على نطاق واسع في مختلف المجالات:

• مقارنة توزيعات: مقارنة أداء مجموعات مختلفة (مثل نتائج اختبارات بين فصول مختلفة، أو مبيعات منتجات مختلفة).
• مراقبة الجودة: تتبع تباين القياسات في عملية الإنتاج وتحديد القيم الخارجة عن السيطرة.
• البحث العلمي: عرض وتلخيص نتائج التجارب والمقارنة بين مجموعات العلاج والتحكم.
• تحليل البيانات المالية: مقارنة تقلبات أسعار الأسهم أو أداء محافظ استثمارية مختلفة.
• تحليل البيانات الاجتماعية: مقارنة توزيعات الدخل أو المستويات التعليمية بين مجموعات سكانية مختلفة.

تفسير التمثيل بالصندوق وطرفيه بفاعلية ومقارنة مجموعات البيانات

لتفسير التمثيل بالصندوق وطرفيه بفاعلية ومقارنة مجموعات البيانات، يجب التركيز على العناصر التالية:

• موقع الصندوق: يشير إلى مركز الـ 50% الوسطى من البيانات. مقارنة مواقع الصناديق تُظهر اختلافات في النزعة المركزية بين المجموعات.
• طول الصندوق (IQR): يشير إلى تشتت الـ 50% الوسطى من البيانات. مقارنة أطوال الصناديق تُظهر اختلافات في تشتت الجزء الأوسط من التوزيعات.
• موقع خط الوسيط داخل الصندوق: يشير إلى مدى تماثل الـ 50% الوسطى من البيانات. إذا كان الوسيط في منتصف الصندوق، يكون التوزيع متماثلًا تقريبًا.
• طول الأطراف: يشير إلى تشتت الجزء العلوي والسفلي من البيانات. مقارنة أطوال الأطراف تُظهر اختلافات في مدى انتشار القيم القصوى والدنيا.
• وجود القيم المتطرفة: يشير إلى قيم غير اعتيادية في البيانات. مقارنة عدد وموقع القيم المتطرفة يُمكن أن يكشف عن اختلافات مهمة بين المجموعات.

الخاتمة

يُعد التمثيل بالصندوق وطرفيه أداة بصرية قوية ومتعددة الاستخدامات لتلخيص البيانات الكمية وفهم توزيعها. من خلال تلخيص خمس قيم إحصائية هامة وعرضها بشكل بياني بسيط، يُمكننا الحصول على رؤى قيمة حول النزعة المركزية، والتشتت، وشكل التوزيع، والقيم المتطرفة في مجموعة البيانات. كما أنه يُعد أداة ممتازة لمقارنة توزيعات متغير واحد عبر مجموعات مختلفة، مما يُسهل عملية تحديد الاختلافات والتشابهات. إن إتقان إنشاء هذا التمثيل البياني وتفسيره بفاعلية يُعد مهارة أساسية للمحللين والباحثين وصناع القرار في مختلف المجالات، حيث يُمكنهم من استخلاص معلومات ذات مغزى من البيانات واتخاذ قرارات أكثر استنارة.