مقدمة

يُمثل مفهوم التطابق في علم الهندسة فكرة التماثل الكامل بين شكلين أو مجسمين. وعند الحديث عن المضلعات، يصبح التطابق بمثابة معيار دقيق للمقارنة والقياس، حيث يشير إلى أن مضلعين متطابقين يمتلكان نفس الشكل تمامًا ونفس الحجم بالضبط. هذا يعني أن كل ضلع في المضلع الأول يقابله ضلع مطابق له في الطول في المضلع الثاني، وأن كل زاوية في المضلع الأول تقابلها زاوية مطابقة لها في القياس في المضلع الثاني. إن فهم شروط التطابق ومعاييره يُعد أساسًا حيويًا في دراسة الأشكال الهندسية وتحليلها، وله تطبيقات واسعة في مجالات متنوعة كالتصميم، والهندسة، والتصنيع، وحتى في فهم الأنماط المتكررة في الطبيعة والفنون. فمن خلال تحديد ما إذا كان مضلعان متطابقين أم لا، نستطيع استنتاج العديد من الخصائص الهندسية لأحدهما بناءً على معرفتنا بخصائص الآخر.

لم يقتصر دور التطابق على مجرد تحديد التشابه التام بين المضلعات، بل امتد ليشمل بناء البراهين الهندسية وتطوير النظريات الرياضية. ففي العديد من البراهين، يتم إثبات تطابق مثلثين أو مضلعين للوصول إلى استنتاجات حول أضلاعهما وزواياهما وعلاقاتهما الهندسية الأخرى. كما أن مفهوم التطابق يُعد أساسًا في تعريف التحويلات الهندسية الحافظة للطول والزاوية، مثل الإزاحة والدوران والانعكاس، والتي تلعب دورًا هامًا في فهم التماثل والحركة في الفضاء. إن إتقان شروط التطابق يُمكننا من التفكير المنطقي في العلاقات الهندسية وإجراء مقارنات دقيقة بين الأشكال المختلفة.

تعريف تطابق المضلعات وشروطه الأساسية

يقال عن مضلعين بأنهما متطابقان (Congruent) إذا أمكن تحويل أحدهما إلى الآخر باستخدام سلسلة من التحويلات الهندسية الحافظة للطول والزاوية، وهي الإزاحة (Translation)، والدوران (Rotation)، والانعكاس (Reflection). بعبارة أخرى، يمكن وضع أحد المضلعين فوق الآخر بحيث ينطبق تمامًا عليه.

لتحقيق تطابق مضلعين، يجب أن يتحقق شرطان أساسيان:

1. تطابق الأضلاع المتناظرة: يجب أن يكون لكل ضلع في المضلع الأول ضلع مقابل له في المضلع الثاني بنفس الطول تمامًا.
2. تطابق الزوايا المتناظرة: يجب أن يكون لكل زاوية في المضلع الأول زاوية مقابلة لها في المضلع الثاني بنفس القياس تمامًا.

يُشار إلى تطابق مضلعين باستخدام الرمز ≅. فإذا كان المضلع ABCD يطابق المضلع EFGH، يُكتب ذلك على النحو التالي: ABCD≅EFGH. ويجب الانتباه إلى ترتيب الرؤوس عند كتابة عبارة التطابق، حيث يشير الترتيب إلى تناظر الأضلاع والزوايا.

معايير تطابق المثلثات

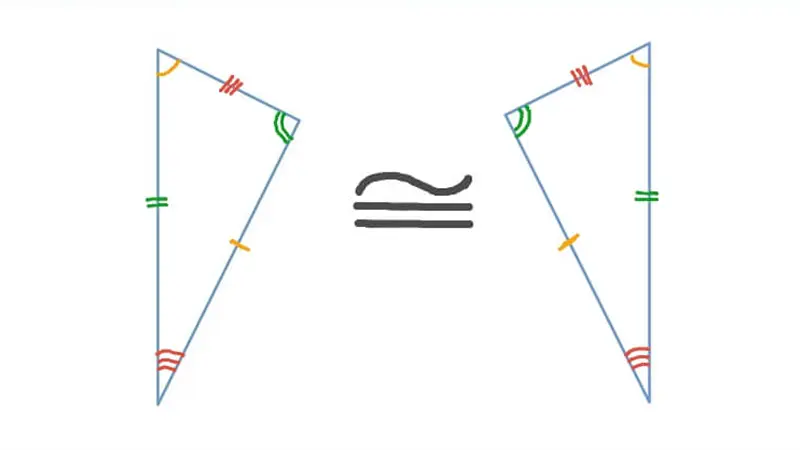
نظرًا لأهمية المثلثات في الهندسة، توجد معايير محددة تُسهل إثبات تطابق مثلثين دون الحاجة إلى إثبات تطابق جميع الأضلاع وجميع الزوايا. هذه المعايير هي:

• ضلع-ضلع-ضلع (SSS): إذا تطابقت أضلاع ثلاثة في مثلث مع أضلاع ثلاثة مناظرة لها في مثلث آخر، فإن المثلثين متطابقان.
• ضلع-زاوية-ضلع (SAS): إذا تطابق ضلعان وزاوية محصورة بينهما في مثلث مع ضلعين وزاوية محصورة بينهما مناظرة لها في مثلث آخر، فإن المثلثين متطابقان.
• زاوية-ضلع-زاوية (ASA): إذا تطابقت زاويتان وضلع واصل بينهما في مثلث مع زاويتين وضلع واصل بينهما مناظرة لها في مثلث آخر، فإن المثلثين متطابقان.
• زاوية-زاوية-ضلع (AAS): إذا تطابقت زاويتان وضلع غير واصل بينهما في مثلث مع زاويتين وضلع غير واصل بينهما مناظرة لها في مثلث آخر، فإن المثلثين متطابقان.
• وتر-ضلع (HL) (خاص بالمثلثات القائمة الزاوية): إذا تطابق وتر وضلع في مثلث قائم الزاوية مع وتر وضلع مناظر لهما في مثلث قائم الزاوية آخر، فإن المثلثين متطابقان.

معايير تطابق الرباعيات

إثبات تطابق رباعيين يتطلب شروطًا أكثر من المثلثات، حيث لا يكفي تطابق الأضلاع فقط أو الزوايا فقط. بشكل عام، لإثبات تطابق رباعيين، يجب إثبات تطابق أربعة أضلاع متناظرة وثلاث زوايا متناظرة (بالترتيب)، أو ثلاثة أضلاع متناظرة وزاويتين متناظرتين محصورتين بين هذه الأضلاع (بالترتيب). لا توجد معايير بسيطة ومحددة لتطابق جميع أنواع الرباعيات كما هو الحال في المثلثات. ومع ذلك، توجد شروط تطابق خاصة لأنواع معينة من الرباعيات:

• تطابق المستطيلين: يتطابق مستطيلان إذا تطابق طولاهما وعرضاهما.
• تطابق المربعين: يتطابق مربعان إذا تطابق طول ضلعيهما.
• تطابق متوازيي الأضلاع: يتطابق متوازيا الأضلاع إذا تطابق ضلعان متجاوران والزاوية المحصورة بينهما، أو إذا تطابقت أضلاعهما الأربعة والزاوية بين ضلعين متجاورين.

معايير تطابق المضلعات العامة

لتحديد ما إذا كان مضلعان لهما أكثر من أربعة أضلاع متطابقين، يجب تحقيق الشرطين الأساسيين للتطابق بشكل كامل:

1. تطابق جميع الأضلاع المتناظرة: يجب أن يكون لكل ضلع في المضلع الأول ضلع مقابل له في المضلع الثاني بنفس الطول.
2. تطابق جميع الزوايا المتناظرة: يجب أن يكون لكل زاوية في المضلع الأول زاوية مقابلة لها في المضلع الثاني بنفس القياس، مع مراعاة ترتيب التناظر بين الرؤوس والأضلاع والزوايا.

لا توجد معايير مختصرة عامة لتطابق المضلعات ذات عدد الأضلاع الأكبر من ثلاثة، كما هو الحال في المثلثات. يجب التحقق من تطابق جميع العناصر المتناظرة.

الخصائص الهندسية المترتبة على التطابق

إذا ثبت تطابق مضلعين، فإن ذلك يعني أن لهما العديد من الخصائص المشتركة:

• نفس المحيط: لأن أضلاعهما المتناظرة متساوية في الطول.
• نفس المساحة: لأنهما يشغلان نفس الحيز من المستوي.
• نفس قياسات الأقطار المتناظرة: لأن الأبعاد الداخلية متطابقة.
• نفس الخصائص الأخرى المتعلقة بالشكل والقياس.

استنتاج هذه الخصائص يوفر الكثير من الجهد في تحليل الأشكال الهندسية، فبمجرد إثبات التطابق، يمكننا تطبيق معرفتنا بأحد المضلعين على الآخر.

تطبيقات تطابق المضلعات في مجالات متنوعة

• التصميم والتصنيع: ضمان تطابق الأجزاء المصنعة لتجميع المنتجات بشكل صحيح ودقيق، مثل قطع غيار السيارات والطائرات والأجهزة الإلكترونية.
• الهندسة المعمارية والإنشاء: تصميم عناصر متكررة في المباني والمنشآت مع ضمان تطابق أبعادها وشكلها لتحقيق الانسجام والاستقرار.
• علم الخرائط والمسح: استخدام المثلثات المتطابقة في عمليات التثليث لتحديد المواقع والمسافات بدقة.
• الروبوتات: برمجة حركات الروبوتات لتكرار مهام محددة بدقة من خلال الاعتماد على تطابق الحركات والأبعاد.
• التعرف على الأنماط: في مجالات مثل معالجة الصور والذكاء الاصطناعي، يُستخدم التطابق في التعرف على الأشكال والأنماط المتكررة.
• الفنون والزخرفة: إنشاء تصاميم متناسقة ومتكررة باستخدام أشكال مضلعة متطابقة.

الخاتمة

يُمثل تطابق المضلعات مفهومًا أساسيًا في علم الهندسة، فهو لغة التماثل الكامل التي تُمكننا من المقارنة الدقيقة بين الأشكال وتحليل خصائصها. إن فهم شروط التطابق ومعاييره المختلفة، سواء للمثلثات أو الرباعيات أو المضلعات العامة، يُعد أداة قوية في بناء البراهين الهندسية وحل المسائل وتطوير النظريات. كما أن تطبيقات مفهوم التطابق تتجلى بوضوح في العديد من المجالات العملية، مما يؤكد على أهميته في حياتنا اليومية وفي التقدم التكنولوجي. إن إتقان هذا المفهوم يُعزز قدرتنا على التفكير المنطقي والهندسي ويُمكننا من تقدير الدقة والتناغم في الأشكال التي تحيط بنا.