حجم الأسطوانة
مقدمة
تُعد الأسطوانة من الأشكال الهندسية ثلاثية الأبعاد الشائعة والمهمة، تتميز ببساطة تركيبها وقاعدتيها الدائريتين المتطابقتين والمتوازيتين وسطحها الجانبي المنحني المنتظم الذي يربط بينهما. يمكن تصور الأسطوانة على أنها منشور خاص ذو قاعدة دائرية. إن فهم مفهوم الأسطوانة وأنواعها (مثل الأسطوانة القائمة والأسطوانة المائلة)، واستيعاب الطريقة الأساسية لحساب حجمها (مساحة القاعدة الدائرية مضروبة في الارتفاع)، يمثل خطوة أساسية في استكشاف الأشكال الدورانية وتطبيقاتها الواسعة في الهندسة الميكانيكية والهندسة المدنية والتصميم الصناعي وفي حياتنا اليومية.
لقد لعبت الأسطوانات دورًا محوريًا في تطور التكنولوجيا والهندسة. فمن الأنابيب والخزانات إلى المحركات والمضخات، تظهر الأشكال الأسطوانية في العديد من الآلات والأدوات والهياكل التي نستخدمها. إن القدرة على حساب حجم الأسطوانة بدقة تمكن المهندسين والمصممين من تقدير السعات، وحساب كميات المواد المطلوبة، وتصميم الأجزاء والأنظمة بكفاءة وفعالية.
مفهوم الأسطوانة وأنواعها المختلفة
مفهوم الأسطوانة: هي مجسم ثلاثي الأبعاد يتكون من:
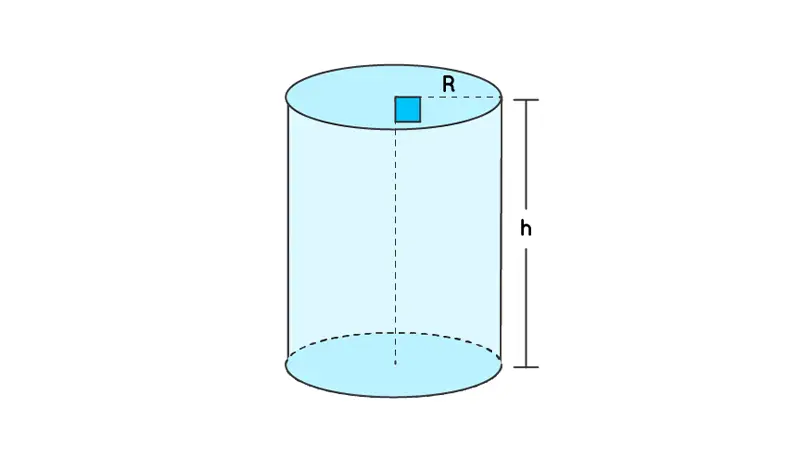
- قاعدتين دائريتين متطابقتين ومتوازيتين: هما الدائرتان اللتان تحددان طرفي الأسطوانة. لكل قاعدة نصف قطر (r).
- سطح جانبي منحني منتظم: يربط بين محيطي القاعدتين الدائريتين. يمكن تخيل هذا السطح على أنه مستطيل تم لفه حول القاعدتين.
- ارتفاع (h): هو المسافة العمودية بين القاعدتين الدائريتين المتوازيتين.
أنواع الأسطوانات:
- الأسطوانة القائمة (Right Cylinder): يكون فيها السطح الجانبي عموديًا على القاعدتين الدائريتين. في هذه الحالة، يكون ارتفاع الأسطوانة هو طول أي خط مستقيم يصل بين نقطتين متناظرتين على محيطي القاعدتين.
- الأسطوانة المائلة (Oblique Cylinder): يكون فيها السطح الجانبي مائلًا على القاعدتين الدائريتين. يكون ارتفاع الأسطوانة هو المسافة العمودية بين القاعدتين، وليس طول أي خط مستقيم على السطح الجانبي.
طريقة حساب حجم الأسطوانة
حجم الأسطوانة، سواء كانت قائمة أو مائلة، يُحسب بنفس الطريقة الأساسية المستمدة من مبدأ حساب حجم المنشور:
حجم الأسطوانة (V) = مساحة القاعدة الدائرية (B) × الارتفاع (h)
حيث:
- V: يمثل حجم الأسطوانة ويُقاس بوحدات مكعبة (مثل سم³، م³).
- B: يمثل مساحة إحدى القاعدتين الدائريتين (بما أنهما متطابقتان) ويُحسب باستخدام قانون مساحة الدائرة: B = πr²، حيث π (باي) ≈ 3.14159 و r هو نصف قطر القاعدة الدائرية ويُقاس بوحدات طول (مثل سم، م).
- h: يمثل ارتفاع الأسطوانة وهو المسافة العمودية بين القاعدتين الدائريتين ويُقاس بوحدات طول (مثل سم، م).
بالتالي، فإن قانون حجم الأسطوانة يصبح: V = πr²h
توضيح العلاقة بين مساحة القاعدة والارتفاع والحجم في الأسطوانة:
يمكن تصور حجم الأسطوانة على أنه عدد الوحدات المكعبة التي يمكن ملء الفراغ الداخلي للأسطوانة بها. تمثل مساحة القاعدة الدائرية عدد الوحدات المربعة التي تغطي إحدى القاعدتين. عند ضرب هذه المساحة في الارتفاع، فإننا نقوم بتكرار هذه الطبقة من الوحدات المربعة بارتفاع الأسطوانة بأكمله، مما ينتج عنه عدد الوحدات المكعبة التي تشغل حيز الأسطوانة.
أمثلة على حساب حجم الأسطوانات:
– أسطوانة قائمة بنصف قطر القاعدة 5 سم وارتفاع 10 سم:
- مساحة القاعدة (B) = π × (5 سم)² = 25π سم²
- الحجم (V) = 25π سم² × 10 سم = 250π سم³ ≈ 785.4 سم³
– أسطوانة مائلة بنصف قطر القاعدة 3 م وارتفاع عمودي 7 م:
- مساحة القاعدة (B) = π × (3 م)² = 9π م²
- الحجم (V) = 9π م² × 7 م = 63π م³ ≈ 197.9 م³
ملاحظة هامة: عند حساب حجم الأسطوانة المائلة، يجب التأكد من استخدام الارتفاع العمودي بين القاعدتين وليس طول أي خط على السطح الجانبي المائل.
أهمية فهم حجم الأسطوانة وتطبيقاتها المتنوعة
فهم كيفية حساب حجم الأسطوانة أمرًا بالغ الأهمية وله تطبيقات واسعة في مختلف المجالات:
الهندسة الميكانيكية:
- حساب حجم أسطوانات المحركات والمضخات والضواغط لتقدير السعات والأداء.
- تصميم الأنابيب والخراطيم وحساب كمية السوائل أو الغازات التي يمكن أن تحملها.
- تقدير حجم الأجزاء الأسطوانية المصنعة لتقدير كمية المواد الخام المطلوبة.
الهندسة المدنية:
- حساب حجم الأنابيب المستخدمة في أنظمة الصرف الصحي والمياه.
- تقدير سعة الخزانات والصوامع الأسطوانية لتخزين السوائل والمواد الصلبة.
- حساب حجم الأعمدة الأسطوانية المستخدمة في دعم الهياكل.
الكيمياء والهندسة الكيميائية:
- حساب حجم الأوعية والمفاعلات الأسطوانية المستخدمة في العمليات الكيميائية.
- تقدير حجم الغازات أو السوائل المحفوظة في أسطوانات.
التصميم الصناعي والتعبئة والتغليف:
- تصميم العلب والعبوات الأسطوانية (مثل علب المشروبات والأطعمة) وحساب سعاتها لتحديد كمية المنتج.
- تقدير كمية المواد الخام اللازمة لتصنيع الأسطوانات.
الطب:
- حساب حجم الأنابيب المستخدمة في الأجهزة الطبية.
- تقدير حجم بعض الأعضاء أو الأورام التقريبية الشكل الأسطواني باستخدام تقنيات التصوير الطبي.
الحياة اليومية:
- تقدير سعة الأكواب والأواني والبراميل الأسطوانية.
- فهم كمية السوائل أو المواد التي يمكن تخزينها في حاويات أسطوانية الشكل.
الرياضيات والتعليم:
- فهم حجم الأسطوانة هو أساس لفهم مفاهيم الحجوم للأشكال الدورانية الأخرى مثل المخروط والكرة.
- تطوير مهارات التفكير المكاني والتصور ثلاثي الأبعاد.
- تطبيق المفاهيم الرياضية في حل مشكلات عملية.
الخاتمة
يظل مفهوم حجم الأسطوانة وطريقة حسابه من الأساسيات الهامة في عالم الهندسة والأبعاد الثلاثية. من خلال العلاقة البسيطة بين مساحة القاعدة الدائرية والارتفاع، نتمكن من فهم وقياس الفراغ الذي تشغله هذه الأشكال الدورانية المنتظمة، مما يفتح الباب أمام تطبيقات عملية واسعة في مختلف جوانب حياتنا الهندسية والصناعية والعلمية. إن القدرة على تصور الأسطوانة وتحليل أبعادها وحساب حجمها بدقة تمثل مهارة قيمة تساهم في تصميم وبناء عالمنا بكفاءة وفعالية. مع استمرار تطور التكنولوجيا وتزايد استخدام الأشكال الأسطوانية في مختلف الصناعات، سيبقى فهم حجم الأسطوانة ذا أهمية قصوى.


