مقدمة

النظام العشري هو نظام عددي يستخدم الأساس 10، ويُعتبر من أكثر الأنظمة العددية استخدامًا في الحياة اليومية وفي العلوم والتكنولوجيا. يعتمد النظام العشري على عشرة أرقام هي: 0، 1، 2، 3، 4، 5، 6، 7، 8، 9. يُعتبر النظام العشري النظام الأساسي الذي يُستخدم لتمثيل الأعداد في معظم الثقافات والحضارات. في هذا البحث، سنتناول تعريف النظام العشري وأهميته وتاريخه وتمثيل الأعداد فيه والعمليات الحسابية التي يمكن تنفيذها باستخدام هذا النظام.

تعريف النظام العشري

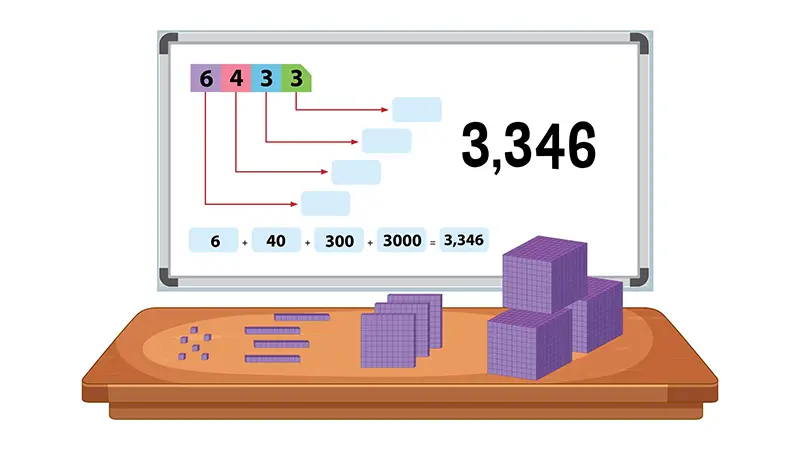
النظام العشري، أو Decimal System، هو نظام عددي يعتمد على الأساس 10، حيث يُمثل الأعداد باستخدام عشرة أرقام (0، 1، 2، 3، 4، 5، 6، 7، 8، 9). تُعتبر القيم المكانية للأرقام في النظام العشري أساسية لفهم كيفية تمثيل الأعداد. على سبيل المثال، الرقم 123 في النظام العشري يُعبر عن 1×100 + 2×10 + 3×1.

أهمية النظام العشري

الاستخدام اليومي

يُعتبر النظام العشري النظام الأساسي الذي يُستخدم في الحياة اليومية لتمثيل الأعداد وإجراء العمليات الحسابية. يمكن أن يساعد ذلك في تسهيل التفاعل مع الأعداد وفهمها واستخدامها بشكل فعّال.

العلوم والتكنولوجيا

يُستخدم النظام العشري بشكل واسع في العلوم والتكنولوجيا، حيث يُعتبر النظام الأساسي الذي يُستخدم في الحسابات العلمية والهندسية والمالية. يمكن أن يساعد ذلك في تحقيق الدقة والكفاءة في العمليات الحسابية والمعادلات العلمية.

التعليم

يُعتبر النظام العشري النظام الأساسي الذي يُدرّس في المدارس والجامعات، حيث يُعتبر من الأنظمة العددية الأساسية التي يجب على الطلاب فهمها واستخدامها في دراساتهم الأكاديمية.

تاريخ النظام العشري

الأصول القديمة

يعود تاريخ النظام العشري إلى الحضارات القديمة مثل الحضارة المصرية والحضارة البابلية، حيث كانوا يستخدمون أنظمة عددية تعتمد على الأساس 10. يُعتقد أن استخدام الأصابع العشرة لليدين في العد كان سببًا في تبني النظام العشري.

الرياضيات الهندية

تطور النظام العشري بشكل كبير في الهند القديمة، حيث قام العلماء والرياضيون الهنود بتطوير النظام العشري الحديث واستخدام الأرقام العشرية التي نعرفها اليوم. يُعتبر العالم الهندي براهماجوبتا من أبرز العلماء الذين ساهموا في تطوير النظام العشري في القرن السابع الميلادي.

الانتشار في العالم الإسلامي

انتقل النظام العشري إلى العالم الإسلامي من خلال العلماء والرياضيين الذين نقلوا المعرفة الهندية إلى الحضارة الإسلامية. قام العلماء المسلمون بتطوير النظام العشري واستخدامه في الحسابات الرياضية والفلكية.

الانتشار في أوروبا

انتقل النظام العشري إلى أوروبا خلال العصور الوسطى من خلال العلماء والرياضيين الذين نقلوا المعرفة من العالم الإسلامي إلى أوروبا. يُعتبر ليوناردو فيبوناتشي من أبرز العلماء الذين ساهموا في نشر النظام العشري في أوروبا من خلال كتابه “كتاب الحساب” الذي نشر في القرن الثالث عشر الميلادي.

تمثيل الأعداد في النظام العشري

الأعداد الصحيحة

يتم تمثيل الأعداد الصحيحة في النظام العشري باستخدام سلسلة من الأرقام العشرية (0، 1، 2، 3، 4، 5، 6، 7، 8، 9). على سبيل المثال، العدد 567 في النظام العشري يُمثل بالصيغة 5×100 + 6×10 + 7×1.

الأعداد السالبة

يتم تمثيل الأعداد السالبة في النظام العشري باستخدام علامة السالب (-) قبل العدد. على سبيل المثال، العدد -123 في النظام العشري يُمثل بالصيغة -1×100 – 2×10 – 3×1.

الأعداد العشرية

يتم تمثيل الأعداد العشرية في النظام العشري باستخدام الفاصلة العشرية (.) لتفصل بين الجزء الصحيح والجزء العشري من العدد. على سبيل المثال، العدد 45.67 في النظام العشري يُمثل بالصيغة 4×10 + 5×1 + 6×0.1 + 7×0.01.

العمليات الحسابية في النظام العشري

الجمع

يتم تنفيذ عملية الجمع في النظام العشري بإضافة الأعداد مباشرةً وفقًا للقيم المكانية للأرقام. على سبيل المثال، جمع العددين 123 و456 في النظام العشري يُعطي الناتج 579. تُعتبر عملية الجمع في النظام العشري أساسية وسهلة التنفيذ.

الطرح

يتم تنفيذ عملية الطرح في النظام العشري بطرح الأعداد مباشرةً وفقًا للقيم المكانية للأرقام. على سبيل المثال، طرح العدد 123 من العدد 456 في النظام العشري يُعطي الناتج 333. تُعتبر عملية الطرح في النظام العشري أساسية وسهلة التنفيذ.

الضرب

يتم تنفيذ عملية الضرب في النظام العشري بضرب الأعداد مباشرةً وفقًا للقيم المكانية للأرقام. على سبيل المثال، ضرب العددين 12 و34 في النظام العشري يُعطي الناتج 408. تُعتبر عملية الضرب في النظام العشري فعالة في تنفيذ العمليات الحسابية المعقدة.

القسمة

يتم تنفيذ عملية القسمة في النظام العشري بقسمة الأعداد مباشرةً وفقًا للقيم المكانية للأرقام. على سبيل المثال، قسمة العدد 144 على العدد 12 في النظام العشري يُعطي الناتج 12. تُعتبر عملية القسمة في النظام العشري فعالة في تقسيم الأعداد بدقة.

تطبيقات النظام العشري

الحسابات اليومية

يُستخدم النظام العشري بشكل واسع في الحسابات اليومية مثل التسوق، دفع الفواتير، وإدارة المال. يمكن أن يساعد النظام العشري في تسهيل العمليات الحسابية اليومية وتحقيق الدقة في الحسابات.

العلوم والهندسة

يُستخدم النظام العشري بشكل واسع في العلوم والهندسة، حيث يُعتبر النظام الأساسي الذي يُستخدم في الحسابات العلمية والهندسية. يمكن أن يساعد النظام العشري في تحقيق الدقة والكفاءة في العمليات الحسابية والمعادلات العلمية.

التعليم

يُعتبر النظام العشري النظام الأساسي الذي يُدرّس في المدارس والجامعات، حيث يُعتبر من الأنظمة العددية الأساسية التي يجب على الطلاب فهمها واستخدامها في دراساتهم الأكاديمية. يمكن أن يساعد النظام العشري في تعزيز مهارات الحساب والتفكير الرياضي لدى الطلاب.

الحوسبة

يُستخدم النظام العشري في الحوسبة لتمثيل الأعداد وإجراء العمليات الحسابية. على الرغم من أن النظام الثنائي يُستخدم بشكل أساسي في الحواسيب، إلا أن النظام العشري يُستخدم أيضًا لتمثيل الأعداد وتقديم البيانات بشكل يسهل فهمه.

التحويل بين الأنظمة العددية

التحويل من النظام العشري إلى النظام الثنائي

يتم تحويل الأعداد من النظام العشري إلى النظام الثنائي باستخدام طريقة القسمة المتكررة على 2. يتم تقسيم العدد العشري على 2 وحساب الباقي، ثم يتم تقسيم الناتج على 2 مرة أخرى وحساب الباقي، وهكذا حتى يتم الحصول على الناتج 0. تُجمع الأرقام المتبقية في الاتجاه العكسي لتكوين العدد الثنائي.

التحويل من النظام الثنائي إلى النظام العشري

يتم تحويل الأعداد من النظام الثنائي إلى النظام العشري باستخدام طريقة الضرب بالأعداد الأسية. يتم ضرب كل رقم ثنائي بقيمته في الأساس 2 ورفع الأساس إلى قوة معينة بناءً على موقع الرقم في السلسلة. تُجمع النتائج للحصول على العدد العشري المكافئ.

التحويل بين الأنظمة الأخرى

يمكن أيضًا تحويل الأعداد بين النظام العشري والأنظمة العددية الأخرى مثل النظام الثماني والنظام الستة عشري. يتم استخدام طرق رياضية معينة لتحقيق هذه التحويلات بدقة.

خاتمة

النظام العشري هو نظام عددي يستخدم الأساس 10، ويُعتبر من أكثر الأنظمة العددية استخدامًا في الحياة اليومية وفي العلوم والتكنولوجيا. يعتمد النظام العشري على عشرة أرقام هي: 0، 1، 2، 3، 4، 5، 6، 7، 8، 9. من خلال فهم تمثيل الأعداد في النظام العشري والعمليات الحسابية فيه وتطبيقاته والتحويل بين الأنظمة العددية، يمكننا تحسين قدرتنا على استخدام هذه التقنية بشكل فعال وتحقيق الفوائد المرجوة منها.