مقدمة

تُعد التحويلات الهندسية من الركائز الأساسية في علم الهندسة، حيث تصف الطرق التي يمكن بها تغيير موقع شكل هندسي أو حجمه أو اتجاهه. ومن بين هذه التحويلات الهندسية الهامة يأتي مفهوم الإزاحة (أو الانسحاب)، الذي يمثل تحريك جميع نقاط الشكل بنفس المسافة وفي نفس الاتجاه. فالإزاحة لا تُغير من شكل أو حجم أو اتجاه الشكل الأصلي، بل تنقله ببساطة من مكان إلى آخر في المستوى أو الفضاء. إن فهم الإزاحة وخصائصها وتمثيلها وتطبيقاتها يُعد أمرًا ضروريًا لفهم العديد من المفاهيم الهندسية والفنية والعلمية.

تعريف الإزاحة وخصائصها الأساسية

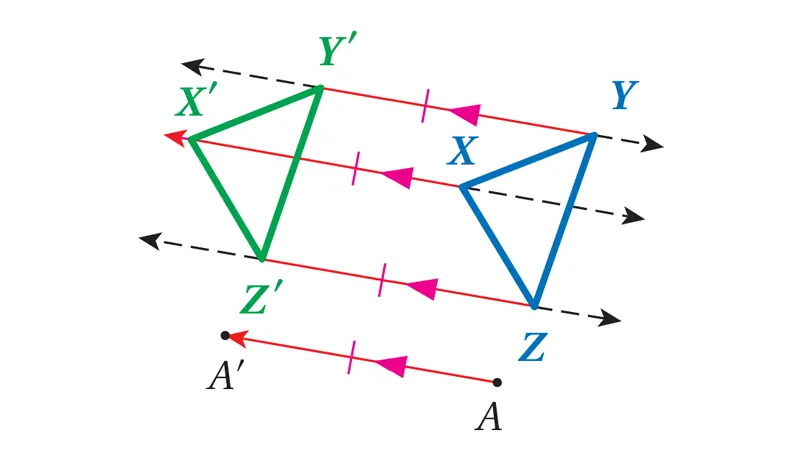
الإزاحة (Translation) هي تحويل هندسي ينقل كل نقطة من نقاط الشكل الأصلي بنفس المسافة وفي نفس الاتجاه المحدد. يمكن تصور الإزاحة على أنها انزلاق للشكل بأكمله دون تدويره أو قلبه أو تغيير حجمه.

تتميز الإزاحة بعدة خصائص أساسية وهامة:

1. الحفاظ على المسافة: المسافة بين أي نقطتين في الشكل الأصلي تساوي المسافة بين صورتيهما في الشكل المزاح. بمعنى آخر، لا تتغير أبعاد الشكل الأصلي بعد الإزاحة.
2. الحفاظ على قياس الزوايا: قياس أي زاوية في الشكل الأصلي يساوي قياس الزاوية المناظرة لها في الشكل المزاح.
3. الحفاظ على الاتجاه (التوجه): لا تُغير الإزاحة من اتجاه الشكل. فإذا كان ترتيب رؤوس الشكل الأصلي في اتجاه عقارب الساعة، فإن ترتيب رؤوس صورته المزاحة سيكون أيضًا في اتجاه عقارب الساعة.
4. توازي القطع المستقيمة: أي قطعة مستقيمة في الشكل الأصلي تكون موازية ومساوية في الطول للقطعة المستقيمة المناظرة لها في الشكل المزاح.
5. توازي المستقيمات: إذا كان مستقيمان متوازيين في الشكل الأصلي، فإنهما سيبقيان متوازيين بعد الإزاحة.

تمثيل الإزاحة

يمكن تمثيل الإزاحة بعدة طرق:

1. باستخدام متجه الإزاحة: يتم تحديد الإزاحة باستخدام متجه (أ، ب) حيث يمثل “أ” مقدار الإزاحة الأفقية (إلى اليمين إذا كان موجبًا وإلى اليسار إذا كان سالبًا)، ويمثل “ب” مقدار الإزاحة الرأسية (إلى الأعلى إذا كان موجبًا وإلى الأسفل إذا كان سالبًا).
2. في المستوى الإحداثي: إذا كانت لدينا نقطة (س، ص) في المستوى الإحداثي وتمت إزاحتها بمتجه الإزاحة (أ، ب)، فإن صورة هذه النقطة بعد الإزاحة ستكون النقطة (س + أ، ص + ب). يتم تطبيق هذا التحويل على جميع نقاط الشكل الأصلي للحصول على صورته المزاحة.

أنواع الإزاحة

يمكن تصنيف الإزاحة بناءً على اتجاه الحركة:

1. إزاحة أفقية: تحدث عندما يكون متجه الإزاحة على الصورة (أ، 0)، أي أن الشكل يتحرك فقط في الاتجاه الأفقي (إلى اليمين أو اليسار) دون أي حركة رأسية.
2. إزاحة رأسية: تحدث عندما يكون متجه الإزاحة على الصورة (0، ب)، أي أن الشكل يتحرك فقط في الاتجاه الرأسي (إلى الأعلى أو الأسفل) دون أي حركة أفقية.
3. إزاحة مائلة: تحدث عندما يكون متجه الإزاحة على الصورة (أ، ب) حيث يكون كل من “أ” و “ب” قيمًا غير صفرية، مما يعني أن الشكل يتحرك في اتجاه مائل يجمع بين الحركة الأفقية والرأسية.

الإزاحة في الفضاء ثلاثي الأبعاد

يمكن تطبيق مفهوم الإزاحة أيضًا في الفضاء ثلاثي الأبعاد. في هذه الحالة، يتم تحديد الإزاحة باستخدام متجه إزاحة ثلاثي الأبعاد (أ، ب، ج)، حيث يمثل “أ” مقدار الإزاحة على محور السينات، ويمثل “ب” مقدار الإزاحة على محور الصادات، ويمثل “ج” مقدار الإزاحة على محور العينات. إذا كانت لدينا نقطة (س، ص، ع) في الفضاء ثلاثي الأبعاد وتمت إزاحتها بالمتجه (أ، ب، ج)، فإن صورتها ستكون النقطة (س + أ، ص + ب، ع + ج).

تطبيقات الإزاحة في الحياة اليومية والعلوم المختلفة

تظهر الإزاحة في العديد من التطبيقات العملية في حياتنا اليومية وفي مختلف المجالات العلمية والتكنولوجية:

1. الرسومات الحاسوبية والتحريك: تُستخدم الإزاحة على نطاق واسع في مجال الرسومات الحاسوبية والتحريك لتحريك الأجسام والشخصيات على الشاشة.
2. علم الروبوتات: تعتمد الروبوتات على الإزاحة لتحريك أجزائها وتنفيذ المهام المختلفة.
3. خطوط الإنتاج في المصانع: يتم استخدام الإزاحة لتحريك المنتجات أو الأجزاء من محطة عمل إلى أخرى على طول خط الإنتاج.
4. علم الفيزياء: يمكن وصف حركة جسم يتحرك في خط مستقيم بسرعة ثابتة بأنها إزاحة.
5. ألعاب الفيديو: حركة الشخصيات والأشياء في ألعاب الفيديو تعتمد بشكل كبير على مفهوم الإزاحة.
6. الملاحة والخرائط: عند تحريك خريطة أو تحريك مؤشر على خريطة، فإننا نقوم بعملية إزاحة.
7. تصميم الأنماط والزخارف: يمكن إنشاء أنماط وزخارف متكررة باستخدام مفهوم الإزاحة لتكرار شكل معين.

الإزاحة والتطابق

تُعتبر الإزاحة تحويلًا يحافظ على التطابق. هذا يعني أن الشكل الناتج عن الإزاحة يكون مطابقًا تمامًا للشكل الأصلي من حيث الحجم والشكل والاتجاه. لذلك، يمكن اعتبار الإزاحة نوعًا من أنواع التحويلات الصلبة (Rigid Transformations) التي لا تغير من خصائص الشكل الهندسي.

أمثلة على الإزاحة

• عندما تحرك قطعة شطرنج على لوحة الشطرنج، فإنك تقوم بعملية إزاحة.
• عندما يسير شخص في خط مستقيم، فإن حركته تمثل إزاحة.
• حركة المصعد من طابق إلى آخر هي مثال على إزاحة رأسية.

خاتمة

في الختام، يمكننا القول بأن الإزاحة هي تحويل هندسي أساسي ينقل جميع نقاط الشكل بنفس المسافة وفي نفس الاتجاه، دون تغيير شكله أو حجمه أو اتجاهه. لقد استعرضنا في هذا البحث تعريف الإزاحة وخصائصها المختلفة، وكيفية تمثيلها باستخدام المتجهات وفي الإحداثيات، بالإضافة إلى أنواع الإزاحة وتطبيقاتها المتنوعة في الحياة اليومية والعلوم المختلفة.