مقدمة

في سياق دراسة المعادلات الجبرية، تُعد المعادلات التي تتضمن القيمة المطلقة (Absolute Value) من المواضيع التي تُضيف بُعدًا جديدًا ومثيرًا للتفكير الجبري. فالقيمة المطلقة لا تعني فقط إزالة الإشارة السالبة من العدد، بل تُشير في جوهرها إلى المسافة التي يبعدها العدد عن الصفر على خط الأعداد، بغض النظر عن الاتجاه. هذا المفهوم الجوهري يُفسر سبب وجود حلين محتملين لمعظم المعادلات التي تتضمن القيمة المطلقة، أحدهما موجب والآخر سالب، أو في بعض الأحيان لا يوجد حل على الإطلاق. إن فهم خصائص القيمة المطلقة وتطبيقها في حل المعادلات يتطلب تفكيرًا منهجيًا، ويُسهم في تطوير مهارات التحليل المنطقي والتعامل مع حالات متعددة. تُعد هذه المعادلات خطوة مهمة في مسيرة تعلم الجبر، حيث تُقدم تحديات تُثري الفهم الرياضي وتُجهز الطلاب لمعادلات ومسائل أكثر تعقيدًا في مجالات الرياضيات المتقدمة والعلوم التطبيقية.

مفهوم القيمة المطلقة وخصائصها

القيمة المطلقة لعدد حقيقي هي المسافة بين هذا العدد والصفر على خط الأعداد. تُرمز القيمة المطلقة للعدد x بالرمز ∣x∣. رياضيًا، تُعرّف القيمة المطلقة كما يلي:

• ∣x∣=x إذا كان x≥0 (أي إذا كان x عددًا موجبًا أو صفرًا).
• ∣x∣=−x إذا كان x<0 (أي إذا كان x عددًا سالبًا). في هذه الحالة، نضرب العدد السالب في سالب لجعله موجبًا، لأن المسافة دائمًا موجبة.

أمثلة:

• ∣5∣=5 (المسافة بين 5 والصفر هي 5 وحدات).
• ∣−5∣=5 (المسافة بين -5 والصفر هي 5 وحدات).
• ∣0∣=0 (المسافة بين 0 والصفر هي 0 وحدات).

خصائص القيمة المطلقة الأساسية:

1. الناتج دائمًا غير سالب: ∣x∣≥0 لأي عدد حقيقي x.
2. التماثل: ∣x∣=∣−x∣.
3. المساواة التربيعية: ∣x∣2=x
4. خاصية الضرب: ∣xy∣=∣x∣∣y∣.
5. خاصية القسمة: ∣x/y​∣=∣y∣/∣x∣​ بشرط ≠ y   
6. متراجحة المثلث (Triangle Inequality): ∣x+y∣≤∣x∣+∣y∣. هذه الخاصية مهمة في دراسة المتراجحات وليس المعادلات بشكل مباشر.

المبدأ الأساسي لحل المعادلات التي تتضمن القيمة المطلقة

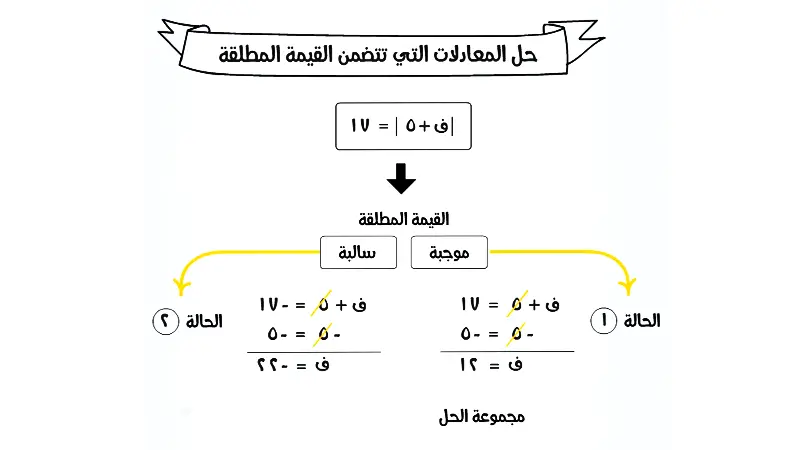
يكمن المبدأ الأساسي في تحويل المعادلة التي تتضمن القيمة المطلقة إلى معادلتين خطيتين أو أكثر. عندما يكون لدينا معادلة بالشكل ∣ax+b∣=c:

1. الحالة الأولى: إذا كان ما داخل القيمة المطلقة موجبًا أو صفرًا، فإنه يساوي الطرف الأيمن مباشرةً. ax+b=c
2. الحالة الثانية: إذا كان ما داخل القيمة المطلقة سالبًا، فإن معاكسه (أي سالب ما داخله) يساوي الطرف الأيمن. وهذا يعني أن ما داخله يساوي سالب الطرف الأيمن. ax+b=−c

شرط هام: قبل تطبيق هذا المبدأ، يجب التأكد من أن الطرف الأيمن للمعادلة (c) موجب أو صفر.

• إذا كان c<0 (عدد سالب)، فلا يوجد حل للمعادلة ∣ax+b∣=c، لأن القيمة المطلقة لا يمكن أن تكون سالبة.

خطوات حل المعادلات التي تتضمن القيمة المطلقة

لحل معادلة تتضمن القيمة المطلقة، يمكن اتباع الخطوات المنهجية التالية:

1. عزل تعبير القيمة المطلقة: يجب أن يكون تعبير القيمة المطلقة (الحد الذي يحتوي على علامة القيمة المطلقة) وحده في أحد طرفي المعادلة. إذا كانت هناك أعداد ثابتة مضافة أو مطروحة أو مضروبة أو مقسومة على تعبير القيمة المطلقة، يجب التخلص منها أولًا باستخدام العمليات العكسية.

مثال: في المعادلة 2∣x−1∣+5=11

• نطرح 5 من الطرفين: 2∣x−1∣=6
• نقسم على 2: ∣x−1∣=3

2. التحقق من إشارة الطرف الأيمن: بعد عزل تعبير القيمة المطلقة، انظر إلى الطرف الأيمن من المعادلة (العدد الثابت).

• إذا كان موجبًا (>0)، تابع إلى الخطوة 3 (سيكون هناك حلان).
• إذا كان صفرًا (=0)، تابع إلى الخطوة 3 (سيكون هناك حل واحد فقط).
  • إذا كان سالبًا (<0)، توقف! لا يوجد حل للمعادلة.

مثال: في المعادلة ∣x−1∣=3، الطرف الأيمن هو 3 (موجب)، لذا نتابع. مثال لعدم وجود حل: ∣x+2∣=−5 (لا يوجد حل).

3. إنشاء معادلتين خطيتين: بناءً على المبدأ الأساسي، قسّم المعادلة إلى معادلتين خطيتين عاديتين:

• المعادلة الأولى: ما داخل القيمة المطلقة يساوي الطرف الأيمن الموجب.
• المعادلة الثانية: ما داخل القيمة المطلقة يساوي الطرف الأيمن السالب.

مثال: من ∣x−1∣=3، نحصل على:

• المعادلة 1: x−1=3
• المعادلة 2: x−1=−3

4. حل كل معادلة خطية على حدة: استخدم طرق حل المعادلات الخطية العادية لإيجاد قيمة المتغير في كلتا المعادلتين.

مثال:

• للمعادلة 1: x−1=3⇒x=3+1⇒x=4
• للمعادلة 2: x−1=−3⇒x=−3+1⇒x=−2

5. التحقق من الحلول (اختياري ولكنه موصى به): عوض كل حل من الحلول التي حصلت عليها في المعادلة الأصلية للتأكد من صحتها.

مثال: المعادلة الأصلية 2∣x−1∣+5=11

• عندما x=4: 2∣4−1∣+5=2∣3∣+5=2(3)+5=6+5=11. (صحيح)
• عندما x=−2: 2∣−2−1∣+5=2∣−3∣+5=2(3)+5=6+5=11. (صحيح)

أمثلة تطبيقية متنوعة

لتعزيز الفهم، دعونا نستعرض أمثلة إضافية تغطي حالات مختلفة:

مثال 1: معادلة ذات حل واحد (عندما يكون الطرف الأيمن صفرًا):

حل المعادلة: ∣3x+6∣=0

1. عزل تعبير القيمة المطلقة: (معزول بالفعل)
2. التحقق من الإشارة: الطرف الأيمن هو 0.
3. إنشاء معادلة خطية واحدة: بما أن الناتج 0، لا يوجد فرق بين +0 و -0. 3x+6=0
4. حل المعادلة: 3x=−6 x= (3/−6)​ x=−2
5. التحقق: ∣3(−2)+6∣=∣−6+6∣=∣0∣=0. (صحيح)

مثال 2: معادلة لا يوجد لها حل:

حل المعادلة: ∣x+4∣+2=−1

1. عزل تعبير القيمة المطلقة: ∣x+4∣=−1−2 ∣x+4∣=−3
2. التحقق من الإشارة: الطرف الأيمن هو -3 (سالب).
3. النتيجة: لا يوجد حل لهذه المعادلة، لأن القيمة المطلقة لا يمكن أن تكون سالبة.

مثال 3: معادلة تتضمن تعبيرات جبرية معقدة داخل القيمة المطلقة:

حل المعادلة: ∣2x−7∣=x+1

1. عزل تعبير القيمة المطلقة: (معزول بالفعل)
2. التحقق من الإشارة: هنا، الطرف الأيمن هو تعبير جبري (x+1). يجب أن نفرض أن x+1≥0، أي x≥−1. إذا كانت الحلول التي نحصل عليها لا تحقق هذا الشرط، فيجب رفضها.
3. إنشاء معادلتين خطيتين:
   • المعادلة 1: 2x−7=x+1
   • المعادلة 2: 2x−7=−(x+1)
4. حل كل معادلة:
   • للمعادلة 1: 2x−x=1+7 x=8 التحقق من الشرط: هل 8≥−1؟ نعم. إذن هذا حل صحيح.
   • للمعادلة 2: 2x−7=−x−1 2x+x=−1+7 3x=6 x=2 التحقق من الشرط: هل 2≥−1؟ نعم. إذن هذا حل صحيح.
5. الحلول: x=8 و x=2.

تطبيقات المعادلات التي تتضمن القيمة المطلقة

تجد المعادلات التي تتضمن القيمة المطلقة تطبيقاتها في العديد من المجالات، خاصة تلك التي تتعلق بالمسافة أو الانحراف عن قيمة معينة:

• المسافة: في الهندسة والفيزياء، تُستخدم القيمة المطلقة لحساب المسافات أو الفروقات.
  • مثال: إذا كان متوسط درجة الحرارة 20 درجة مئوية، وتريد معرفة درجات الحرارة التي تنحرف بمقدار 5 درجات عن المتوسط. يمكن تمثيل ذلك بالمعادلة ∣T−20∣=5.
• التحكم في الجودة: في التصنيع، قد يكون هناك هامش خطأ مسموح به في أبعاد المنتج.
  • مثال: إذا كان طول جزء معين يجب أن يكون 10 سم، بهامش خطأ 0.1 سم. يمكن التعبير عن ذلك بالمعادلة ∣L−10∣=0.1.
• الفيزياء: في حساب الأخطاء المطلقة أو تحديد النطاقات المسموح بها للقياسات.
• الإحصاء: في حساب الانحراف المطلق أو في بعض نماذج تحليل البيانات.

الخاتمة

تُعد المعادلات التي تتضمن القيمة المطلقة إضافة مهمة ومثيرة للاهتمام في منهاج الجبر، فهي تُعزز الفهم العميق لمفهوم المسافة الرياضي وتُجبر الطلاب على التفكير في السيناريوهات المتعددة للحل. من خلال تحويل هذه المعادلات إلى معادلتين خطيتين عاديتين، والتحقق من إشارة الطرف الأيمن، يمكن للطلاب فك رموز هذه المعادلات بفعالية. إن إتقان هذا النوع من المعادلات لا يُعزز فقط المهارات الجبرية، بل يُنمي أيضًا القدرة على التحليل المنطقي والتعامل مع الحالات المختلفة، وهي مهارات ضرورية في مجالات أكاديمية ومهنية أوسع. تُشكل هذه المعادلات جسرًا حيويًا نحو فهم أعمق للوظائف والمتراجحات التي تتضمن القيمة المطلقة، وتُجهز المتعلم لتحديات رياضية أكثر تعقيدًا في المستقبل.