مقدمة

في عالم الرياضيات، تُعد المعادلات الخطية أدوات أساسية لوصف العلاقات التي تتغير فيها كمية واحدة بمعدل ثابت بالنسبة لأخرى. من بين الأشكال المتعددة التي يمكن أن تتخذها هذه المعادلات، تبرز صيغة الميل والمقطع (Slope-Intercept Form) كواحدة من أكثرها قوة ووضوحًا لتمثيل العلاقات الخطية بيانيًا. هذه الصيغة، التي تُكتب على الشكل y=mx+b، تُقدم مباشرةً معلومات حيوية عن الخط المستقيم الذي تُمثله: ميله (انحداره) والنقطة التي يقطع فيها المحور الرأسي. إن القدرة على تحويل أي معادلة خطية إلى هذه الصيغة، ثم استخدامها لرسم الخط بدقة وسهولة، تفتح آفاقًا واسعة لفهم سلوك الكميات المتغيرة بصريًا. هذا الفهم البصري ليس مجرد مهارة أكاديمية، بل هو أداة تحليلية أساسية في مجالات مثل الفيزياء، الاقتصاد، والهندسة، حيث تُترجم العلاقات العددية المجردة إلى صور مرئية تُسهل اتخاذ القرارات وحل المشكلات المعقدة.

مراجعة مفهوم المعادلة الخطية وصيغة الميل والمقطع

قبل الغوص في التمثيل البياني، من الضروري استذكار أساسيات المعادلة الخطية وصيغة الميل والمقطع.

المعادلة الخطية: هي معادلة جبرية تُشكل خطًا مستقيمًا عند تمثيلها بيانيًا. سميت “خطية” لأن أعلى أس لأي متغير فيها هو واحد. لا تتضمن هذه المعادلات متغيرات مرفوعة لقوى أكبر من واحد (مثل x²)، أو مضروبة في بعضها البعض (مثل xy)، أو موجودة في المقام أو تحت الجذر التربيعي.

صيغة الميل والمقطع (y=mx+b): تُعد هذه الصيغة من أهم طرق كتابة المعادلات الخطية، وتُعرف أيضًا بالصيغة الأساسية للدالة الخطية. في هذه الصيغة:

• y: هو المتغير التابع (المخرج)، وقيمته تعتمد على قيمة x.
• x: هو المتغير المستقل (المدخل)، ويمكننا اختيار قيم له.
• m: يمثل الميل (Slope) للخط. الميل هو قياس لانحدار الخط واتجاهه. إذا كان m موجبًا، يتجه الخط للأعلى من اليسار إلى اليمين. إذا كان m سالبًا، يتجه الخط للأسفل. إذا كان m صفرًا، يكون الخط أفقيًا. من المهم أن نتذكر أن الميل هو نسبة التغير الرأسي إلى التغير الأفقي بين أي نقطتين على الخط.
• b: يمثل الجزء المقطوع من المحور y (y-intercept). وهي النقطة التي يتقاطع فيها الخط مع المحور y. قيمة x عند هذه النقطة تكون دائمًا صفرًا، لذا فإن إحداثيات الجزء المقطوع من المحور y هي دائمًا (0,b).

مثال: في المعادلة y=3x+2:

• الميل (m) يساوي 3.
• الجزء المقطوع من المحور y (b) يساوي 2. هذا يعني أن الخط يمر بالنقطة (2,0).

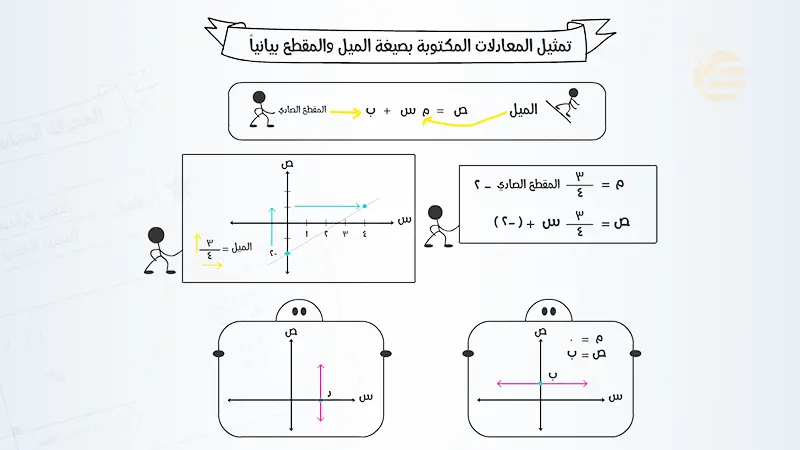
خطوات تمثيل المعادلات المكتوبة بصيغة الميل والمقطع بيانيًا

تُعد طريقة الميل والمقطع واحدة من أسرع وأسهل الطرق لرسم خط مستقيم، وذلك لأنها تُعطينا نقطة بداية واضحة (الجزء المقطوع من المحور y) ودليلًا على كيفية التحرك لإيجاد نقاط إضافية (الميل).

الخطوات الأساسية:

1. التأكد من أن المعادلة في صيغة الميل والمقطع: يجب أن تكون المعادلة على شكل y=mx+b. إذا لم تكن كذلك، يجب إعادة ترتيبها جبريًا لتحويلها إلى هذا الشكل. وهذا يتضمن عزل المتغير y في أحد طرفي المعادلة.
   • مثال على إعادة الترتيب: إذا كانت لدينا المعادلة 2x+y=5: نطرح 2x من كلا الطرفين لعزل y: y=−2x+5 الآن أصبحت المعادلة في صيغة الميل والمقطع، حيث m=−2 و b=5.
2. تحديد الجزء المقطوع من المحور y (b): ابحث عن قيمة b في المعادلة y=mx+b. هذه القيمة تُمثل الإحداثي y للنقطة التي يقطع فيها الخط المحور y. ارسم هذه النقطة على المستوى الإحداثي الديكارتي. ستكون دائمًا على المحور y (المحور الرأسي)، وإحداثياتها (0,b).
   • مثال: في y=−2x+5, قيمة b=5. ارسم النقطة (5,0).
3. تحديد الميل (m) واستخدامه لإيجاد نقطة ثانية: تذكر أن الميل هو “التغير في y على التغير في x” (يُعرف أيضًا بالارتفاع على المسافة الأفقية).
   • إذا كان الميل عددًا صحيحًا (مثل 3 أو -2): اكتبه ككسر بوضع 1 في المقام (مثل 3/1 أو −2/1). البسط يُمثل التغير الرأسي، والمقام يُمثل التغير الأفقي.
   • إذا كان الميل كسرًا (مثل 2/3 أو −1/4): البسط يُمثل التغير الرأسي، والمقام يُمثل التغير الأفقي.
   • من نقطة الجزء المقطوع من المحور y التي رسمتها في الخطوة 2:
     • التغير الرأسي (البسط): تحرك عموديًا للأعلى إذا كان البسط موجبًا، أو للأسفل إذا كان البسط سالبًا.
     • التغير الأفقي (المقام): تحرك أفقيًا لليمين إذا كان المقام موجبًا، أو لليسار إذا كان المقام سالبًا (في معظم الحالات، يكون المقام موجبًا).
   • ارسم النقطة الثانية التي توصلت إليها.
   • مثال: في y=−2x+5, الميل m=−2. يمكن كتابته كـ −2/1. من النقطة (0,5):
     • تحرك وحدتين للأسفل (لأن البسط -2).
     • ثم تحرك وحدة واحدة لليمين (لأن المقام 1). ستصل إلى النقطة (1,3). ارسم هذه النقطة.

4. رسم الخط المستقيم: باستخدام مسطرة، ارسم خطًا مستقيمًا يمر عبر النقطتين اللتين رسمتهما. تأكد من تمديد الخط في كلا الاتجاهين ليشمل سهمين عند الأطراف، للإشارة إلى أنه يمتد إلى ما لا نهاية.
   • مثال: ارسم خطًا مستقيمًا يمر بالنقطتين (0,5) و (1,3).

أمثلة تفصيلية لتمثيل المعادلات بيانياً

دعونا نطبق الخطوات على أمثلة متنوعة.

مثال 1: معادلة بميل موجب

مثل بيانيًا المعادلة: y=(2/1)​x+3

1. صيغة الميل والمقطع؟ نعم، هي بالفعل في هذه الصيغة.
2. الجزء المقطوع من المحور y (b): b=3. ارسم النقطة (0,3).
3. الميل (m): m=2/1​. من النقطة (0,3):
   • تحرك وحدة واحدة للأعلى (التغير الرأسي).
   • ثم تحرك وحدتين لليمين (التغير الأفقي). ستصل إلى النقطة (2,4). ارسم هذه النقطة.
4. رسم الخط: ارسم خطًا مستقيمًا يمر بالنقطتين (0,3) و (2,4).

مثال 2: معادلة بميل سالب

مثل بيانيًا المعادلة: y=−3x+1

1. صيغة الميل والمقطع؟ نعم، هي كذلك.
2. الجزء المقطوع من المحور y (b): b=1. ارسم النقطة (0,1).
3. الميل (m): m=−3. يمكن كتابته كـ −3/1. من النقطة (0,1):
   • تحرك 3 وحدات للأسفل (لأن البسط سالب).
   • ثم تحرك وحدة واحدة لليمين (المقام موجب). ستصل إلى النقطة (1,−2). ارسم هذه النقطة.
4. رسم الخط: ارسم خطًا مستقيمًا يمر بالنقطتين (0,1) و (1,−2).

مثال 3: معادلة تتطلب إعادة ترتيب

مثل بيانيًا المعادلة: 4x−2y=8

1. صيغة الميل والمقطع؟ لا، ليست كذلك. يجب عزل y.
   • اطرح 4x من كلا الطرفين: −2y=−4x+8
   • اقسم كلا الطرفين على -2: y=(−2/−4x)+(−2/8)​
   • بسط: y=2x−4 الآن أصبحت في صيغة الميل والمقطع، حيث m=2 و b=−4.
2. الجزء المقطوع من المحور y (b): b=−4. ارسم النقطة (0,−4).
3. الميل (m): m=2. يمكن كتابته كـ 2/1. من النقطة (0,−4):
   • تحرك وحدتين للأعلى.
   • ثم تحرك وحدة واحدة لليمين. ستصل إلى النقطة (1,−2). ارسم هذه النقطة.
4. رسم الخط: ارسم خطًا مستقيمًا يمر بالنقطتين (0,−4) و (1,−2).

حالات خاصة في التمثيل البياني

الخطوط الأفقية: المعادلات على شكل y=c (حيث c ثابت).

• في هذه الحالة، الميل هو صفر (m=0).
• الجزء المقطوع من المحور y هو c.
• الخط يكون أفقيًا تمامًا ويمر عبر النقطة (0,c) على المحور y.
• مثال: y=5. ارسم خطًا أفقيًا يمر عبر y=5 على المحور الرأسي.

الخطوط الرأسية: المعادلات على شكل x=c (حيث c ثابت).

• هذه المعادلات لا يمكن كتابتها بصيغة الميل والمقطع لأن ميلها غير معرف (خط رأسي).
• يجب تمثيلها ببساطة عن طريق رسم خط رأسي يمر عبر النقطة (c,0) على المحور x.
• مثال: x=−3. ارسم خطًا رأسيًا يمر عبر x=−3 على المحور الأفقي.

أهمية التمثيل البياني لصيغة الميل والمقطع

تُعد القدرة على تمثيل المعادلات الخطية بيانياً باستخدام صيغة الميل والمقطع ذات أهمية قصوى لعدة أسباب:

• الفهم البصري المباشر: تُقدم هذه الصيغة رؤية فورية لانحدار الخط ونقطة بدايته على المحور الرأسي. هذا الفهم البصري يُسهل تفسير العلاقة بين المتغيرات.
• تحليل معدل التغير: الميل (m) يُمثل معدل التغير الثابت في العلاقة. من الرسم البياني، يمكننا بصريًا تقدير مدى سرعة أو بطء تغير المتغير التابع بالنسبة للمتغير المستقل.
• التنبؤ: يمكن استخدام الخطوط المرسومة للتنبؤ بقيم المتغيرات خارج نطاق البيانات المتاحة.
• تحديد الحلول المشتركة: عند تمثيل نظام من المعادلات الخطية بيانيًا، فإن نقطة تقاطع الخطوط (إن وجدت) تُمثل الحل المشترك للنظام.
• تطبيقات عملية واسعة: تُستخدم المعادلات الخطية في نماذج لا حصر لها من الواقع. على سبيل المثال:
  • في الاقتصاد: لتمثيل منحنيات العرض والطلب.
  • في الفيزياء: لتمثيل الحركة بسرعة ثابتة (المسافة مقابل الزمن).
  • في الأعمال: لتخطيط التكاليف والإيرادات (نقطة التعادل).
  • في الحياة اليومية: حساب تكلفة خدمة معينة بناءً على استخدام ثابت ورسوم أساسية (مثل فاتورة الكهرباء).

الخاتمة

إن تمثيل المعادلات الخطية المكتوبة بصيغة الميل والمقطع بيانيًا ليس مجرد تمرين رياضي، بل هو مهارة تحليلية أساسية تُمكننا من رؤية وتفسير العلاقات العددية المعقدة. هذه الصيغة تُقدم لنا مفتاحًا بصريًا لخصائص الخط المستقيم: ميله الذي يُحدد انحداره، والجزء المقطوع من المحور y الذي يُشير إلى نقطة بدايته. من خلال إتقان هذه الطريقة، يكتسب الطلاب أداة قوية لتحليل البيانات، التنبؤ بالاتجاهات، وحل المشكلات في مختلف المجالات العلمية والعملية. تُسهم هذه المهارة في بناء فهم أعمق للجبر وتطبيقاته الواقعية، مما يُعزز من قدرة الفرد على التفكير النقدي واتخاذ قرارات مستنيرة بناءً على فهم واضح للعلاقات الكمية.