مقدمة

في قلب علم الجبر، تكمن المعادلات الخطية كأحد المفاهيم الأساسية التي تُشكل حجر الزاوية لفهم العلاقات بين الكميات. هذه المعادلات، التي تُعرف بكونها ذات أس واحد للمتغيرات، تُرسم على شكل خط مستقيم عند تمثيلها بيانياً. إن القدرة على تمثيل المعادلات الخطية بيانياً ليست مجرد مهارة تقنية، بل هي نافذة تُطل على فهم أعمق للعلاقات المتغيرة في العالم من حولنا. يتيح لنا هذا التمثيل رؤية النمط الذي يربط بين الكميات، وتحديد نقاط التقاطع، واستشراف سلوك المتغيرات بصريًا. إنه يُترجم الأرقام والرموز المجردة إلى صور مرئية ملموسة، مما يُسهم في تعزيز الفهم والتحليل وحل المشكلات في مجالات متنوعة تتجاوز حدود الرياضيات، مثل العلوم والهندسة والاقتصاد. يهدف هذا البحث إلى استكشاف مفهوم المعادلات الخطية، وطرق تمثيلها بيانياً، وخصائص الخط المستقيم الناتج، بالإضافة إلى أهمية هذا التمثيل في فهم وتطبيق المفاهيم الرياضية على أرض الواقع.

مفهوم المعادلة الخطية وخصائصها

ما هي المعادلة الخطية؟ المعادلة الخطية هي معادلة جبرية تُشكل، عند رسمها بيانياً، خطاً مستقيماً. تُسمى “خطية” لأن أعلى أس للمتغيرات فيها هو واحد. لا تتضمن هذه المعادلات أي متغيرات مرفوعة لقوى أكبر من واحد (مثل x² أو y³)، ولا متغيرات مضروبة في بعضها البعض (مثل xy)، ولا متغيرات في المقام أو تحت الجذر التربيعي (مثل  √x​).

الشكل العام للمعادلة الخطية: يمكن التعبير عن المعادلة الخطية في عدة أشكال، أشهرها:

• الصيغة القياسية (Standard Form): Ax+By=C حيث A, B, و C هي ثوابت، و x و y هما المتغيران. يجب أن يكون A و B لا يساويان صفرًا في نفس الوقت.
• صيغة الميل والمقطع (Slope-Intercept Form): y=mx+b تُعد هذه الصيغة الأكثر شيوعًا وسهولة في التمثيل البياني. هنا:
  • m يمثل الميل (Slope): وهو يُحدد انحدار الخط واتجاهه.
  • b يمثل الجزء المقطوع من المحور y (y-intercept): وهي النقطة التي يتقاطع فيها الخط مع المحور y.

خصائص الخط المستقيم:

• الميل (m):
  • الميل الموجب (m>0): الخط يتجه للأعلى من اليسار إلى اليمين (يزداد y كلما زاد x).
  • الميل السالب (m<0): الخط يتجه للأسفل من اليسار إلى اليمين (يتناقص y كلما زاد x).
  • الميل الصفري (m=0): الخط أفقي (معادلة على شكل y=b).
  • الميل غير المعرف (Undefined Slope): الخط رأسي (معادلة على شكل x=c).
• الجزء المقطوع من المحور y (b): يُشير إلى النقطة (0,b) حيث يقطع الخط المحور y.
• الجزء المقطوع من المحور x (x-intercept): هي النقطة التي يقطع فيها الخط المحور x. تُحسب بوضع y=0 في المعادلة وحل المعادلة لإيجاد قيمة x.

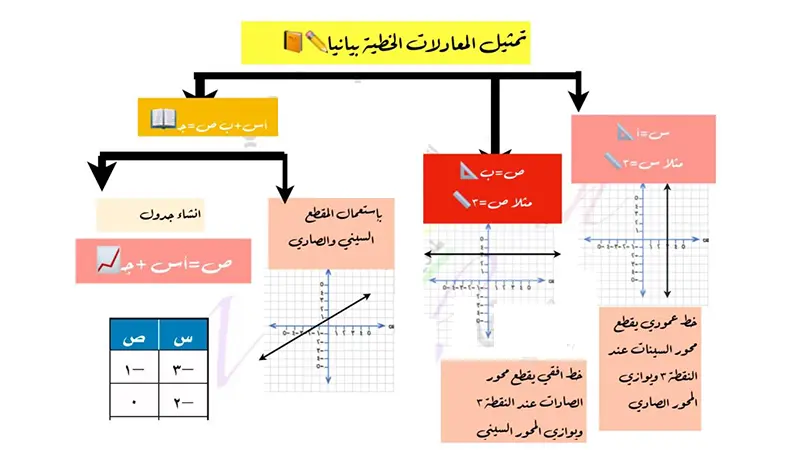
طرق تمثيل المعادلات الخطية بيانياً

هناك عدة طرق شائعة لتمثيل المعادلات الخطية بيانياً:

1. طريقة النقاط (Plotting Points Method):

تُعد هذه الطريقة الأكثر أساسية ومباشرة، وتصلح لأي معادلة خطية.

الخطوات:

1. اختر قيمًا لـ x: عادةً ما يكون اختيار 3 قيم على الأقل جيدًا لضمان دقة الرسم، مع مراعاة اختيار قيم سهلة للتعويض (مثل 0، 1، -1).
2. عوض القيم في المعادلة لإيجاد قيم y المقابلة: كل زوج من (x,y) يمثل نقطة على الخط.
3. ارسم النقاط: حدد كل زوج مرتب كنقطة في المستوى الإحداثي الديكارتي.
4. وصل النقاط: ارسم خطًا مستقيمًا يمر عبر جميع النقاط. يجب أن تكون النقاط على استقامة واحدة.

مثال: مثل المعادلة y=2x+1 بيانياً.

1. اختيار قيم لـ x:
   • إذا كان x=0: y=2(0)+1=1⇒(0,1)
   • إذا كان x=1: y=2(1)+1=3⇒(1,3)
   • إذا كان x=−2: y=2(−2)+1=−4+1=−3⇒(−2,−3)
2. رسم النقاط وتوصيلها: (تصور شبكة إحداثيات مرسوم عليها النقاط (0,1), (1,3), (-2,-3) وخط مستقيم يمر بها).
3. طريقة الميل والمقطع (Slope-Intercept Method):

تُعد هذه الطريقة فعالة جدًا عندما تكون المعادلة في صيغة الميل والمقطع (y=mx+b).

الخطوات:

1. حدد الجزء المقطوع من المحور y (b): ارسم النقطة (0,b) على المحور y.
2. استخدم الميل (m) لإيجاد نقطة أخرى: تذكر أن الميل هو “التغير في y على التغير في x” (الارتفاع على المسافة الأفقية).
   • إذا كان الميل كسرًا مثل ​ (rise/run)، فابدأ من نقطة الجزء المقطوع من المحور y وانتقل بمقدار “الصعود” عموديًا (لأعلى إذا كان موجبًا، لأسفل إذا كان سالبًا) ثم بمقدار “الجريان” أفقيًا (لليمين إذا كان موجبًا، لليسار إذا كان سالبًا) لتحديد النقطة الثانية.
   • إذا كان الميل عددًا صحيحًا، اجعله كسرًا بوضعه فوق 1 (مثل m=1/m​).
3. ارسم خطًا مستقيمًا يمر بالنقطتين.

مثال: مثل المعادلة y=(3/2)​x−2 بيانياً.

1. الجزء المقطوع من المحور y: b=−2. ارسم النقطة (0,−2).
2. الميل: m=3/2​. من النقطة (0,−2)، اصعد وحدتين لأعلى ثم تحرك 3 وحدات لليمين. ستصل إلى النقطة (3,0).

3. ارسم الخط: (تصور شبكة إحداثيات مرسوم عليها النقطتين (0,-2) و (3,0) وخط مستقيم يمر بهما).
4. طريقة الأجزاء المقطوعة (Intercepts Method):

تُعد هذه الطريقة مفيدة بشكل خاص عندما تكون المعادلة في الصيغة القياسية (Ax+By=C)، ولكنها قابلة للتطبيق على أي معادلة خطية.

الخطوات:

1. إيجاد الجزء المقطوع من المحور y: ضع x=0 في المعادلة وحلها لإيجاد قيمة y. النقطة هي (0,y).
2. إيجاد الجزء المقطوع من المحور x: ضع y=0 في المعادلة وحلها لإيجاد قيمة x. النقطة هي (x,0).
3. ارسم النقطتين ووصل بينهما بخط مستقيم.

مثال: مثل المعادلة 3x+4y=12 بيانياً.

1. الجزء المقطوع من المحور y (x=0): 3(0)+4y=12 4y=12 y=3⇒(0,3)
2. الجزء المقطوع من المحور x (y=0): 3x+4(0)=12 3x=12 x=4⇒(4,0)
3. ارسم الخط: (تصور شبكة إحداثيات مرسوم عليها النقطتين (0,3) و (4,0) وخط مستقيم يمر بهما).

حالات خاصة للمعادلات الخطية

• الخطوط الأفقية: المعادلات على شكل y=c (حيث c ثابت).
  • الميل هو صفر.
  • الخط يقطع المحور y عند النقطة (0,c) ولا يقطع المحور x (إلا إذا كان c=0).
  • مثال: y=5. (تصور خطًا أفقيًا يمر عبر y=5).
• الخطوط الرأسية: المعادلات على شكل x=c (حيث c ثابت).
  • الميل غير معرف.
  • الخط يقطع المحور x عند النقطة (c,0) ولا يقطع المحور y (إلا إذا كان c=0).
  • مثال: x=−3. (تصور خطًا رأسيًا يمر عبر x=−3).

أهمية التمثيل البياني للمعادلات الخطية

لا يقتصر تمثيل المعادلات الخطية بيانياً على كونه تمرينًا رياضيًا، بل له أهمية كبيرة في:

• الفهم البصري للعلاقات: يُسهل فهم العلاقة بين المتغيرات بصريًا، مما يُساعد على استيعاب كيفية تأثير التغير في متغير على الآخر.
• تحديد الحلول المشتركة (أنظمة المعادلات): عند رسم معادلتين خطيتين على نفس المستوى، يمكن تحديد نقطة تقاطعهما، والتي تمثل الحل المشترك للنظام.
• تحليل البيانات: تُستخدم النماذج الخطية لتمثيل وتوقع البيانات في مجالات مثل الاقتصاد والعلوم الاجتماعية.
• التنبؤ: يمكن استخدام الخطوط لتقدير قيم مجهولة بناءً على الاتجاه الموضح في الرسم البياني.
• فهم الميل والمقطع: يُعزز التمثيل البياني فهم معنى الميل (معدل التغير) والجزء المقطوع من المحور y (القيمة الابتدائية أو الأساسية).
• تطبيقات عملية: في تصميم المباني (خطوط البناء)، رسم الخرائط، تحليل مسارات الأجسام المتحركة، وغيرها.

تحديات شائعة عند التمثيل البياني وكيفية تجنبها

قد يواجه الطلاب بعض التحديات عند تمثيل المعادلات الخطية بيانياً:

• الأخطاء الحسابية: التعويض الخاطئ للقيم أو الأخطاء في تبسيط المعادلات.
  • الحل: استخدام الآلة الحاسبة للتحقق، والقيام بالخطوات ببطء وتركيز.
• عدم الدقة في الرسم: رسم النقاط بشكل غير دقيق أو عدم توصيلها بخط مستقيم تمامًا.
  • الحل: استخدام مسطرة وقلم رصاص مدبب، والتأكد من تحديد النقاط بدقة على المحاور.
• اختيار قيم غير مناسبة لـ x: اختيار قيم كبيرة جدًا أو صغيرة جدًا مما يجعل الرسم صعبًا.
  • الحل: اختيار قيم بسيطة وصغيرة نسبيًا، بما في ذلك الصفر والأعداد السالبة والموجبة لتغطية نطاق أوسع.
• عدم تحويل المعادلة إلى صيغة الميل والمقطع: إذا لم تكن المعادلة في هذه الصيغة، قد يكون من الأسهل تحويلها قبل استخدام طريقة الميل والمقطع.
  • الحل: مراجعة خطوات إعادة ترتيب المعادلات.
• الخلط بين المحاور: وضع قيم x على المحور y والعكس.
  • الحل: تذكر دائمًا أن الزوج المرتب هو (y,x) وأن المحور الأفقي هو x والمحور الرأسي هو y.

الخاتمة

يُعد تمثيل المعادلات الخطية بيانياً مهارة أساسية في الرياضيات تُترجم العلاقات الجبرية المجردة إلى صور بصرية ملموسة. إنه يُمكننا من استكشاف الخصائص الأساسية للخطوط المستقيمة مثل الميل والجزء المقطوع من المحور y، ويُقدم فهمًا عميقًا لكيفية تغير الكميات بشكل خطي. من خلال إتقان الطرق المختلفة للتمثيل البياني، يكتسب الطلاب أداة قوية للتحليل وحل المشكلات، ليس فقط في سياق الجبر، بل في مجالات واسعة من العلوم والهندسة والاقتصاد. إن القدرة على قراءة وتفسير الرسوم البيانية تُصبح لغة عالمية للتواصل العلمي والتحليلي، مما يُبرز أهمية هذا المفهوم كبوابة لتعميق الفهم الرياضي وتطبيقاته العملية التي تُسهم في تقدم المعرفة وحل تحديات العالم الحقيقي.