مقدمة

تُعد الدوال المنطقية (Logical Functions)، أو البوابات المنطقية (    )، اللبنات الأساسية التي تقوم عليها جميع الأنظمة الرقمية الحديثة، بدءًا من أبسط الدوائر الإلكترونية وصولًا إلى أعقد الحواسيب العملاقة وشبكات الإنترنت. إنها تمثل التجسيد العملي لمبادئ المنطق البولياني (Boolean Logic)، الذي يتعامل مع القيمتين الثنائيتين: الصواب (True أو 1) والخطأ (False أو 0). من خلال تجميع هذه الدوال المنطقية بطرق محددة، يمكن تصميم دوائر إلكترونية قادرة على اتخاذ القرارات المنطقية، وتنفيذ العمليات الحسابية، وتخزين البيانات، والتحكم في تدفق المعلومات. إن فهم طبيعة الدوال المنطقية، وأنواعها الأساسية، وكيفية عملها، وكيفية تمثيلها جبريًا ومنطقيًا، يمثل أساسًا ضروريًا لكل من يتعامل مع مجالات الهندسة الكهربائية وهندسة الحاسوب وعلوم الحاسوب.

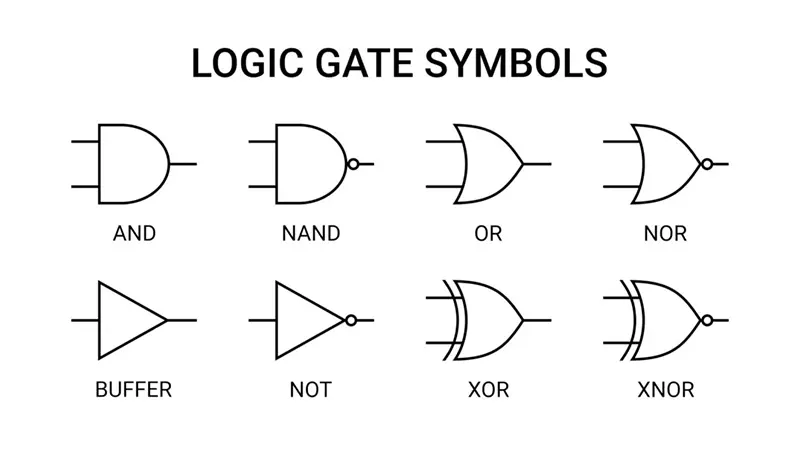
تعمل الدوال المنطقية على أساس مدخلات منطقية (إشارة كهربائية تمثل 0 أو 1) وتنتج مخرجًا منطقيًا واحدًا بناءً على قاعدة منطقية محددة. هناك عدد قليل من الدوال المنطقية الأساسية التي تشكل حجر الزاوية في تصميم الدوائر الرقمية، مثل دالة “و” (AND)، ودالة “أو” (OR)، ودالة “ليس” (NOT). من خلال دمج هذه الدوال الأساسية، يمكن بناء دوائر منطقية أكثر تعقيدًا لتنفيذ وظائف محددة. كما أن هناك دوال منطقية مشتقة مثل دالة “لا و” (NAND)، ودالة “لا أو” (NOR)، ودالة “أو الحصرية” (XOR)، ودالة “لا أو الحصرية” (XNOR)، والتي توفر مرونة وكفاءة أكبر في تصميم الدوائر.

تعريف الدوال المنطقية وأهميتها في الأنظمة الرقمية

الدالة المنطقية هي دائرة إلكترونية بسيطة لها مدخل واحد أو أكثر ومخرج واحد، وتنفذ عملية منطقية محددة على المدخلات لإنتاج المخرج. تعتمد هذه العمليات المنطقية على مبادئ الجبر البولياني، حيث تمثل المدخلات والمخرجات قيمًا ثنائية (0 أو 1).

تكمن أهمية الدوال المنطقية في الأنظمة الرقمية في:

• بناء الدوائر الرقمية: هي اللبنات الأساسية التي يتم تجميعها لتكوين دوائر أكثر تعقيدًا تقوم بتنفيذ وظائف محددة.
• اتخاذ القرارات المنطقية: تسمح للدوائر الرقمية باتخاذ قرارات بناءً على شروط منطقية محددة.
• تنفيذ العمليات الحسابية: يمكن تجميع الدوال المنطقية لتنفيذ عمليات الجمع والطرح والضرب والقسمة وغيرها من العمليات الحسابية.
• تخزين البيانات: تستخدم الدوال المنطقية في تصميم عناصر الذاكرة الرقمية مثل القلابات (Flip-Flops) والسجلات (Registers).
• التحكم في تدفق المعلومات: تستخدم في تصميم دوائر التحكم التي توجه تدفق البيانات والإشارات داخل النظام الرقمي.
• الواجهة بين الأجهزة: تلعب دورًا في تصميم الدوائر التي تربط بين المكونات المختلفة داخل النظام الرقمي وبين الأنظمة الرقمية المختلفة.

أنواع الدوال المنطقية الأساسية

هناك ثلاث دوال منطقية أساسية تشكل الأساس لتصميم أي دائرة رقمية:

• دالة “و” (AND Gate): تنتج مخرجًا منطقيًا قيمته 1 فقط إذا كانت جميع مدخلاتها المنطقية قيمتها 1. في أي حالة أخرى (إذا كان أحد المدخلات أو كلاهما 0)، يكون المخرج 0.
  • التمثيل الجبري البولياني: Y=A⋅B أو Y=AB
  • جدول الحقيقة: | A | B | Y | |—|—|—| | 0 | 0 | 0 | | 0 | 1 | 0 | | 1 | 0 | 0 | | 1 | 1 | 1 |
  • الرمز المنطقي: يختلف الرمز حسب المعيار، ولكنه عادةً ما يكون على شكل نصف دائرة مستطيلة مع مدخلين ومخرج واحد
• دالة “أو” (OR Gate): تنتج مخرجًا منطقيًا قيمته 1 إذا كان واحد أو أكثر من مدخلاتها المنطقية قيمتها 1. يكون المخرج 0 فقط إذا كانت جميع مدخلاتها 0.
  • التمثيل الجبري البولياني: Y=A+B
  • جدول الحقيقة: | A | B | Y | |—|—|—| | 0 | 0 | 0 | | 0 | 1 | 1 | | 1 | 0 | 1 | | 1 | 1 | 1 |
  • الرمز المنطقي: عادةً ما يكون على شكل هلال مدبب الطرف مع مدخلين ومخرج واحد
• دالة “ليس ” NOT Gate أو Inverter لها مدخل واحد ومخرج واحد. تقوم بعكس قيمة المدخل المنطقي. إذا كان المدخل 1، يكون المخرج 0، وإذا كان المدخل 0، يكون المخرج 1.
  • التمثيل الجبري البولياني: Y=A أو Y=A′
  • جدول الحقيقة: | A | Y | |—|—| | 0 | 1 | | 1 | 0 |
  • الرمز المنطقي: عادةً ما يكون على شكل مثلث يشير إلى اليمين مع دائرة صغيرة في نهايته

أنواع الدوال المنطقية المشتقة

من خلال دمج الدوال المنطقية الأساسية، يمكن اشتقاق دوال منطقية أخرى أكثر تعقيدًا:

• دالة “لا و” (NAND Gate): هي دمج لدالة “و” ودالة “ليس”. تنتج مخرجًا منطقيًا قيمته 0 فقط إذا كانت جميع مدخلاتها 1. في أي حالة أخرى، يكون المخرج 1.
  • التمثيل الجبري البولياني: Y=A⋅B
  • جدول الحقيقة: | A | B | Y | |—|—|—| | 0 | 0 | 1 | | 0 | 1 | 1 | | 1 | 0 | 1 | | 1 | 1 | 0 |
  • الرمز المنطقي: رمز دالة “و” مع دائرة صغيرة في نهايته
• دالة “لا أو” (NOR Gate): هي دمج لدالة “أو” ودالة “ليس”. تنتج مخرجًا منطقيًا قيمته 1 فقط إذا كانت جميع مدخلاتها 0. في أي حالة أخرى (إذا كان أي من المدخلات 1)، يكون المخرج 0.
  • التمثيل الجبري البولياني: Y=A+B​
  • جدول الحقيقة: | A | B | Y | |—|—|—| | 0 | 0 | 1 | | 0 | 1 | 0 | | 1 | 0 | 0 | | 1 | 1 | 0 |
  • الرمز المنطقي: (رمز دالة “أو” مع دائرة صغيرة في نهايته)
• دالة “أو الحصرية” (XOR Gate): تنتج مخرجًا منطقيًا قيمته 1 إذا كانت مدخلاتها المنطقية مختلفة (أحدهما 0 والآخر 1). يكون المخرج 0 إذا كانت المدخلات متماثلة (كلاهما 0 أو كلاهما 1).
  • التمثيل الجبري البولياني: Y=A⊕B=AB+AB
  • جدول الحقيقة: | A | B | Y | |—|—|—| | 0 | 0 | 0 | | 0 | 1 | 1 | | 1 | 0 | 1 | | 1 | 1 | 0 |
  • الرمز المنطقي: (رمز دالة “أو” مع خط منحني إضافي قبل المدخلات)

• دالة “لا أو الحصرية” (XNOR Gate): هي دمج لدالة “أو الحصرية” ودالة “ليس”. تنتج مخرجًا منطقيًا قيمته 1 إذا كانت مدخلاتها المنطقية متماثلة (كلاهما 0 أو كلاهما 1). يكون المخرج 0 إذا كانت المدخلات مختلفة.

• التمثيل الجبري البولياني: Y=A⊕B​=AB+AB
• جدول الحقيقة: | A | B | Y | |—|—|—| | 0 | 0 | 1 | | 0 | 1 | 0 | | 1 | 0 | 0 | | 1 | 1 | 1 |
• الرمز المنطقي: رمز دالة “أو الحصرية” مع دائرة صغيرة في نهايته

تجميع الدوال المنطقية لتكوين دوائر منطقية معقدة

يمكن تجميع الدوال المنطقية الأساسية والمشتقة معًا لتصميم دوائر منطقية أكثر تعقيدًا قادرة على تنفيذ وظائف محددة. يتم ذلك عن طريق ربط مخرج دالة منطقية بمدخل دالة منطقية أخرى. يمكن تمثيل هذه الدوائر باستخدام مخططات الدوائر المنطقية التي توضح كيفية توصيل البوابات المنطقية.

أمثلة على الدوائر المنطقية المعقدة:

• نصف جامع (Half Adder): دائرة منطقية تجمع رقمين ثنائيين وتنتج ناتج الجمع وحمل (Carry). تتكون من دالة “أو الحصرية” (للناتج) ودالة “و” (للحمل).
• جامع كامل (Full Adder): دائرة منطقية تجمع ثلاثة أرقام ثنائية (رقمان والناتج من عملية جمع سابقة) وتنتج ناتج الجمع وحمل. تتكون من دالتين “نصف جامع” ودالة “أو”.
• المقارنات (Comparators): دوائر منطقية تقارن بين قيمتين ثنائيتين وتنتج مخرجًا يشير إلى ما إذا كانت القيمتان متساويتين أو إحداهما أكبر من الأخرى.
• فك الشفرة (Decoders) و الترميز (Encoders): دوائر منطقية تقوم بتحويل المعلومات من شكل إلى آخر.
• الذاكرة (Memory Elements): تستخدم القلابات (Flip-Flops)، وهي دوائر منطقية تعتمد على التغذية الراجعة، لتخزين بت واحد من المعلومات.

دور الدوال المنطقية في تصميم الذاكرة والمعالجات والأنظمة الرقمية الأخرى

تلعب الدوال المنطقية دورًا حيويًا في تصميم المكونات الأساسية للأنظمة الرقمية:

• الذاكرة (Memory): تستخدم القلابات (Flip-Flops)، التي يتم بناؤها باستخدام دوال منطقية مثل “لا و” أو “لا أو”، لتخزين البيانات الثنائية في الذاكرة الرقمية (مثل ذاكرة الوصول العشوائي RAM والذاكرة للقراءة فقط ROM).
• المعالجات (Processors): تعتمد وحدة المعالجة المركزية (CPU) على ملايين من الدوال المنطقية المترابطة لتنفيذ العمليات الحسابية والمنطقية التي تشكل أساس عمل الحاسوب. تشمل هذه العمليات الجمع والطرح والمقارنة والتحكم في تدفق التعليمات.
• الأنظمة الرقمية الأخرى: تستخدم الدوال المنطقية في تصميم مجموعة واسعة من الأنظمة الرقمية الأخرى مثل:
  • أنظمة التحكم الرقمي: في المصانع والأجهزة.
  • أنظمة الاتصالات الرقمية: في الهواتف وشبكات الإنترنت.
  • أنظمة معالجة الإشارات الرقمية: في الصوت والصورة والفيديو.
  • الدوائر المتكاملة (Integrated Circuits – ICs): التي تحتوي على ملايين أو حتى مليارات من الترانزستورات المجمعة لتكوين دوال منطقية معقدة.

الخاتمة

تُعد الدوال المنطقية حجر الزاوية في عالم الحوسبة الرقمية، فهي الأساس الذي تقوم عليه جميع العمليات التي تجعل الأجهزة الرقمية تعمل. من خلال فهم أنواعها الأساسية والمشتقة وكيفية عملها وتمثيلها، ندرك كيف يمكن تجميع هذه اللبنات البسيطة لتكوين دوائر منطقية معقدة قادرة على اتخاذ القرارات وتنفيذ العمليات وتخزين المعلومات والتحكم في الأنظمة الرقمية. إن الدور الحيوي الذي تلعبه الدوال المنطقية في تصميم الذاكرة والمعالجات والأنظمة الرقمية الأخرى يؤكد على أهميتها الأساسية في تشكيل التكنولوجيا الحديثة التي نعتمد عليها في حياتنا اليومية. إن استمرار التطور في مجال تصميم وتصنيع الدوال المنطقية هو ما يدفع عجلة التقدم في عالم الحوسبة والإلكترونيات.