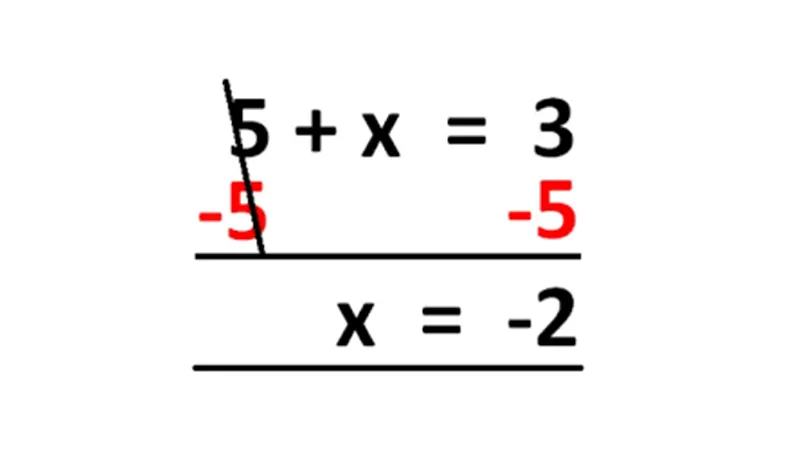
مقدمة

في عالم الرياضيات، تُعد المعادلات الجبرية لبنة أساسية تُستخدم لوصف العلاقات بين الكميات وحل المشكلات في مختلف المجالات، من العلوم والهندسة إلى الاقتصاد والحياة اليومية. وقبل الغوص في تعقيدات المعادلات الأكثر تعقيدًا، لا بد من فهم الأساسيات التي تبدأ بـ المعادلات ذات الخطوة الواحدة (One-Step Equations). هذه المعادلات، على بساطتها، تمثل نقطة انطلاق حاسمة في تعلم الجبر، حيث تُقدم مفهوم المتغيرات والعمليات العكسية بطريقة مباشرة. إنها تُعلمنا كيف يمكننا عزل المتغير المجهول باستخدام عملية رياضية واحدة فقط. تُعد المعادلات ذات الخطوة الواحدة بمثابة البوابة التي يعبر منها الطلاب إلى عالم التفكير الجبري، فهي تُرسخ لديهم فهمًا عميقًا لكيفية التعامل مع الرموز والمتغيرات، وتُمكنهم من بناء أساس قوي لمهارات حل المشكلات التي ستُخدمهم في المراحل المتقدمة من دراسة الرياضيات وما بعدها.

مفهوم المعادلة ذات الخطوة الواحدة ومكوناتها الأساسية

• المعادلة (Equation): في جوهرها، المعادلة هي عبارة رياضية تُظهر أن قيمتين أو تعبيرين متساويان. تُستخدم علامة المساواة (=) لربط الطرفين. على سبيل المثال، في المعادلة x+5=10، فإن الطرف الأيسر (x+5) يساوي الطرف الأيمن (10).
• المتغير (Variable): هو رمز، غالبًا ما يكون حرفًا (مثل x, y, z), يُستخدم لتمثيل قيمة مجهولة أو كمية تتغير. الهدف من حل المعادلة هو إيجاد قيمة هذا المتغير.
• العدد الثابت (Constant): هو قيمة عددية ثابتة لا تتغير في المعادلة. في المعادلة x+5=10, العدد 5 والعدد 10 هما ثابتان.
• المعادلة ذات الخطوة الواحدة: هي معادلة جبرية تتطلب عملية رياضية واحدة فقط (جمع، طرح، ضرب، قسمة) لعزل المتغير وإيجاد قيمته. بمعنى آخر، يمكن حلها في خطوة واحدة.

مبدأ الموازنة في حل المعادلات

الفهم الأساسي لحل أي معادلة، بما في ذلك المعادلات ذات الخطوة الواحدة، هو مبدأ الموازنة (Balancing). هذا المبدأ ينص على أن أي عملية رياضية تُطبق على أحد طرفي المعادلة يجب أن تُطبق أيضًا على الطرف الآخر للحفاظ على المساواة.

تخيل المعادلة كميزان ذو كفتين متساويتين. إذا أضفت وزنًا إلى كفة واحدة، فسوف يختل الميزان. للحفاظ على التوازن، يجب أن تضيف نفس الوزن إلى الكفة الأخرى. وبالمثل، إذا أزلت وزنًا من كفة، يجب أن تزيل نفس الوزن من الكفة الأخرى.

هذا المبدأ هو جوهر استخدام العمليات العكسية (Inverse Operations) لعزل المتغير.

أنواع المعادلات ذات الخطوة الواحدة وكيفية حلها

تُصنف المعادلات ذات الخطوة الواحدة بناءً على العملية الرياضية المستخدمة فيها:

1. معادلات الجمع (Addition Equations)

• الشكل العام: x+a=b
• الهدف: عزل x (جعل x وحده في أحد طرفي المعادلة).
• العملية العكسية: الطرح.
• كيفية الحل: نطرح العدد الثابت (a) من كلا طرفي المعادلة.

مثال: حل المعادلة x+7=15

1. الخطوة 1: لعزل x, نطرح 7 من كلا الطرفين: x+7−7=15−7
2. الخطوة 2: نبسط: x=8

التحقق: 8+7=15, إذن الحل صحيح.

2. معادلات الطرح (Subtraction Equations)

• الشكل العام: x−a=b
• الهدف: عزل x.
• العملية العكسية: الجمع.
• كيفية الحل: نجمع العدد الثابت (a) إلى كلا طرفي المعادلة.

مثال: حل المعادلة x−4=12

1. الخطوة 1: لعزل x, نجمع 4 إلى كلا الطرفين: x−4+4=12+4
2. الخطوة 2: نبسط: x=16

التحقق: 16−4=12, إذن الحل صحيح.

3. معادلات الضرب (Multiplication Equations)

• الشكل العام: ax=b (حيث a و b ثابتان، و  ≠  a 0)
• الهدف: عزل x.
• العملية العكسية: القسمة.
• كيفية الحل: نقسم كلا طرفي المعادلة على العدد الثابت (a) الذي يضرب المتغير.

مثال: حل المعادلة 3X=21

1. الخطوة 1: لعزل x, نقسم كلا الطرفين على 3: 3 3x/= 3/21​
2. الخطوة 2: نبسط:  x= 7

التحقق: 3×7=21, إذن الحل صحيح.

4. معادلات القسمة (Division Equations)

• الشكل العام: x/a​=b (حيث a و b ثابتان، و   ≠  a 0 )
• الهدف: عزل x.
• العملية العكسية: الضرب.
• كيفية الحل: نضرب كلا طرفي المعادلة في العدد الثابت (a) الذي يقسم المتغير.

مثال: حل المعادلة 5/x​=6

1. الخطوة 1: لعزل x, نضرب كلا الطرفين في 5: (5/x​)×5=6×5
2. الخطوة 2: نبسط: x=30

التحقق: 5/30​=6, إذن الحل صحيح.

أهمية المعادلات ذات الخطوة الواحدة في تعلم الجبر

على الرغم من بساطتها، تُقدم المعادلات ذات الخطوة الواحدة فوائد تعليمية جمة تُرسخ فهم الجبر لدى الطلاب:

• بناء المفاهيم الأساسية: تُعد حجر الزاوية لفهم مفهوم المتغيرات، وكيفية تمثيل الكميات المجهولة، والهدف من حل المعادلات.
• فهم العمليات العكسية: تُعلم الطلاب أن لكل عملية رياضية عملية عكسية تُبطلها، وهو مبدأ أساسي يُطبق في حل جميع أنواع المعادلات.
• تطوير التفكير المنطقي: تُشجع الطلاب على التفكير بشكل منهجي في كيفية عزل المتغير خطوة بخطوة.
• التحضير للمراحل المتقدمة: تُعد أساسًا لا غنى عنه لحل المعادلات الأكثر تعقيدًا (ذات الخطوتين، والمتعددة الخطوات)، بالإضافة إلى المعادلات الخطية وغير الخطية.
• تطبيق الموازنة: تُعزز فكرة أن أي تعديل في أحد طرفي المعادلة يجب أن يُعاد تطبيقه على الطرف الآخر للحفاظ على المساواة.
• حل المشكلات الواقعية: على الرغم من أن أمثلتها قد تبدو بسيطة، إلا أن المبادئ المستفادة تُطبق في حل مشكلات واقعية أكثر تعقيدًا تُترجم إلى معادلات جبرية.

أمثلة تطبيقية متنوعة

لتعزيز الفهم، دعونا نستعرض بعض الأمثلة المتنوعة، بما في ذلك الأمثلة التي تتضمن أعدادًا سالبة أو كسورًا:

1. معادلة جمع بأعداد سالبة:

y+(−3)=10

y−3=10 (نُعيد كتابتها لتبسيطها)

y−3+3=10+

3 y=13

2. معادلة طرح بأعداد سالبة:

z−(−5)=7

z+5=7 (نُعيد كتابتها لتبسيطها)

z+5−5=7−5

 z=2

3. معادلة ضرب بكسر: (3/2)​m=8

للتخلص من الكسر، نضرب كلا الطرفين في مقلوب الكسر (2/3​):

2/3​×(3/2)​m =8×2/3​

m=2/24​

m=12

4. معادلة قسمة بعدد سالب: −4/k​=5

−4k/​×(−4)=5×(−4)

k=−20

الخاتمة

تُعد المعادلات ذات الخطوة الواحدة بمثابة المدخل الأولي لعالم الجبر الواسع، فهي تُقدم المبادئ الأساسية لحل المعادلات بطريقة بسيطة ومفهومة. إن إتقان هذه المعادلات لا يُعزز فقط المهارات الرياضية الأساسية، بل يُنمي أيضًا التفكير النقدي والمنطقي، وهما مهارتان حيويتان ليس فقط في الرياضيات ولكن في حل المشكلات بشكل عام. من خلال فهم مبدأ الموازنة، وتطبيق العمليات العكسية، يستطيع الطلاب عزل المتغيرات وإيجاد قيمها بسهولة، مما يُرسخ لديهم الثقة في قدرتهم على التعامل مع تحديات جبرية أكبر. إن الأساس المتين الذي تُبنيه المعادلات ذات الخطوة الواحدة يُعد ضروريًا لنجاح الطلاب في مسيرتهم التعليمية في الرياضيات وما بعدها، فهو يُمكنهم من فك شفرة العلاقات العددية وفهم كيفية عمل العالم من حولهم.