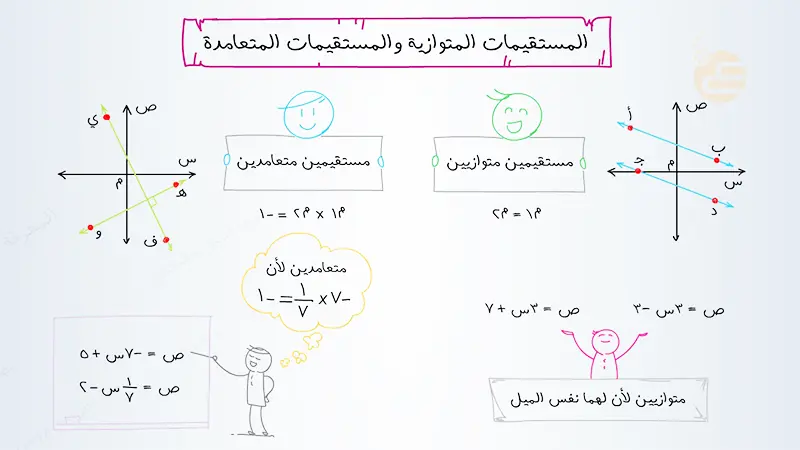
مقدمة

في قلب الهندسة الرياضية، تُعد دراسة العلاقات بين الخطوط المستقيمة أمرًا أساسيًا لفهم الفضاء ثنائي وثلاثي الأبعاد. من بين هذه العلاقات، يبرز مفهوما التوازي (Parallelism) والتعامد (Perpendicularity) كحجر الزاوية الذي تبنى عليه العديد من النظريات والتطبيقات. تُعرف المستقيمات المتوازية بأنها الخطوط التي لا تتقاطع أبدًا مهما امتدت، وتحافظ على مسافة ثابتة بينها، بينما تُشكل المستقيمات المتعامدة زوايا قائمة تمامًا عند نقطة تقاطعها. تتجاوز أهمية هذين المفهومين حدود الفصول الدراسية؛ فهي تُشكل أساسًا لتصميم المباني، وتخطيط المدن، وفهم الظواهر الفيزيائية، وحتى في الفنون والتصميم. إن فهم الخصائص الهندسية والجبرية للمستقيمات المتوازية والمتعامدة يُمكننا من تحليل العلاقات المكانية بدقة، وحل المشكلات الهندسية المعقدة، وبناء أساس رياضي متين يُسهم في فهم أعمق للعالم من حولنا.

تعريف المستقيمات المتوازية

المستقيمات المتوازية هي خطان مستقيمان أو أكثر يقعان في نفس المستوى ولا يتقاطعان أبدًا مهما امتدتا في أي من الاتجاهين. السمة الأساسية للمستقيمات المتوازية هي أنها تحافظ على مسافة ثابتة بينها في جميع النقاط.

الرمز: يُستخدم الرمز ∥ للإشارة إلى التوازي. فإذا كان المستقيم L₁​ موازياً للمستقيم L₂​, يُمكن كتابة ذلك كـ L₁​∥L₂​.

خصائص المستقيمات المتوازية

تُمكننا خصائص المستقيمات المتوازية من التعرف عليها وتحديدها، سواء بصريًا أو جبريًا:

1. عدم التقاطع: هذا هو التعريف الأساسي للمستقيمات المتوازية.
2. المسافة الثابتة: المسافة العمودية بين أي نقطة على أحد المستقيمين المتوازيين والنقطة المقابلة لها على المستقيم الآخر تظل ثابتة دائمًا.
3. الميل المتساوي: في المستوى الإحداثي الديكارتي، إذا كان خطان مستقيمان غير رأسيين متوازيين، فإن ميليهما متساويان تمامًا. هذا هو المفتاح لتحديد التوازي جبريًا.
   • إذا كان ميل الخط الأول هو m₁​ وميل الخط الثاني هو m₂​, وكان الخطان متوازيين، فإن m₁​=m₂​.
4. الخطوط الأفقية والرأسية المتوازية:
   • أي خطين أفقيين (لهما معادلة من الشكل ص يساوي ثابت) يكونان متوازيين. ميل كل منهما يساوي صفرًا.
   • أي خطين رأسيين (لهما معادلة من الشكل س يساوي ثابت) يكونان متوازيين. ميل كل منهما غير معرف.

أمثلة من الواقع

يمكن ملاحظة المستقيمات المتوازية في العديد من العناصر اليومية:

• قضبان السكك الحديدية.
• حواف الطريق المستقيمة.
• خطوط الدفتر أو الورقة المسطرة.
• أضلاع الطاولات المتقابلة.
• أسلاك الكهرباء الممتدة.

المستقيمات المتعامدة وخصائصها

تعريف المستقيمات المتعامدة

المستقيمات المتعامدة هي خطان مستقيمان يتقاطعان مكونين زاوية قائمة تمامًا عند نقطة تقاطعهما. الزاوية القائمة قياسها 90 درجة. عندما يتقاطع خطان ويشكلان زاوية قائمة، فإنهما بالضرورة يشكلان أربع زوايا قائمة عند نقطة التقاطع.

الرمز: يُستخدم الرمز ⊥ للإشارة إلى التعامد. فإذا كان المستقيم L₁​ متعامدًا مع المستقيم L₂​, يُمكن كتابة ذلك كـ L₁​⊥L₂​.

خصائص المستقيمات المتعامدة

تُمكننا خصائص المستقيمات المتعامدة من التعرف عليها وتحديدها:

1. التقاطع بزاوية قائمة: هذا هو التعريف الجوهري للتعامد.
2. الميل المقلوب السالب: في المستوى الإحداثي الديكارتي، إذا كان خطان مستقيمان غير رأسيين ومتعامدين، فإن حاصل ضرب ميليهما يساوي سالب واحد (-1).
   • أي، إذا كان ميل الخط الأول هو m₁​ وميل الخط الثاني هو m₂​, وكان الخطان متعامدين، فإن m₁​ مضروبًا في m₂​ يساوي سالب واحد.
   • بشكل مكافئ، يكون ميل أحد الخطين هو المقلوب السالب لميل الخط الآخر. هذا يعني أننا نقلب الكسر ونغير إشارته. على سبيل المثال، إذا كان ميل أحد الخطوط 2 (مكتوبًا 2 مقسومًا على 1)، فإن ميل الخط المتعامد معه سيكون سالب 1 مقسومًا على 2.
3. الخطوط الأفقية والرأسية: المستقيم الأفقي والمتعامد معه المستقيم الرأسي، يعتبران متعامدين دائمًا. هذه هي الحالة الوحيدة التي لا تنطبق عليها قاعدة حاصل ضرب الميلين يساوي سالب واحد، وذلك بسبب عدم وجود ميل معرف للمستقيم الرأسي.

أمثلة من الواقع

توجد المستقيمات المتعامدة في كل مكان حولنا:

• أركان الغرفة أو الزوايا بين الجدران والأرضية.
• تقاطع الشارع الرئيسي مع الشارع الجانبي في تخطيط المدن.
• تقاطع المحاور س و ص في المستوى الإحداثي الديكارتي.
• زوايا الأبواب والنوافذ وإطارات الصور.
• صليب إشارة المرور.

تحديد العلاقات بين المستقيمات جبريًا

تُعد القدرة على تحديد ما إذا كانت المستقيمات متوازية أو متعامدة أو لا شيء من ذلك باستخدام معادلاتها أو نقاطها مهارة أساسية في الجبر التحليلي.

خطوات التحديد

1. إيجاد ميل كل خط:
   • إذا كانت المعادلة في صيغة الميل والمقطع (ص = م س زائد ب)، فالميل هو العدد م.
   • إذا كانت المعادلة في الصيغة القياسية (أ س زائد ب ص يساوي ج)، يجب إعادة ترتيبها إلى صيغة الميل والمقطع لعزل ص وتحديد الميل. على سبيل المثال، 2 س زائد 4 ص يساوي 8 يمكن تحويلها إلى 4 ص يساوي سالب 2 س زائد 8، ثم ص يساوي سالب 0.5 س زائد 2. في هذه الحالة الميل هو سالب 0.5.
   • إذا كانت لدينا نقطتان على الخط، يمكننا حساب الميل باستخدام صيغة الميل: الميل يساوي (ص2 ناقص ص1) مقسومًا على (س2 ناقص س1).

المقارنة أو الضرب:

• • للتوازي: قارن ميلي الخطين. إذا كانا متساويين، فالمستقيمان متوازيان (مع استثناء الخطوط الرأسية التي لها ميل غير معرف، ولكنها متوازية مع بعضها البعض).
  • للتعامد: اضرب ميلي الخطين. إذا كان حاصل ضربهما يساوي سالب واحد، فالمستقيمان متعامدان (مع استثناء الخطوط الأفقية والرأسية التي هي دائمًا متعامدة).
  • إذا لم ينطبق أي من الشرطين، فالمستقيمان ليسا متوازيين ولا متعامدين، بل متقاطعين بشكل عام.

أمثلة توضيحية

مثال 1: تحديد التوازي

هل الخطان ص = 3 س زائد 7 و ص = 3 س ناقص 2 متوازيان؟

1. ميل الخط الأول م1 = 3.
2. ميل الخط الثاني م2 = 3.
3. بما أن م1 يساوي م2، والخطان غير رأسيين، فالمستقيمان متوازيان.

مثال 2: تحديد التعامد

هل الخطان ص = 2 س زائد 1 و ص = سالب 0.5 س زائد 4 متعامدان؟

1. ميل الخط الأول م1 = 2.
2. ميل الخط الثاني م2 = سالب 0.5.
3. حاصل ضرب الميلين: 2 مضروبًا في سالب 0.5 يساوي سالب 1.
4. بما أن حاصل الضرب يساوي سالب 1، فالمستقيمان متعامدان.

مثال 3: لا متوازيان ولا متعامدان

هل الخطان ص = 4 س زائد 5 و ص = 0.5 س ناقص 1 متوازيان أو متعامدان؟

1. ميل الخط الأول م1 = 4.
2. ميل الخط الثاني م2 = 0.5.
3. هل م1 = م2؟ لا، 4 لا يساوي 0.5. إذن ليسا متوازيين.
4. هل م1 مضروبًا في م2 يساوي سالب 1؟ 4 مضروبًا في 0.5 يساوي 2. لا يساوي سالب 1. إذن ليسا متعامدين.
5. الخطان ليسا متوازيين ولا متعامدين.

كتابة معادلات المستقيمات المتوازية والمتعامدة

تُعد القدرة على كتابة معادلة خط مستقيم يفي بمتطلبات التوازي أو التعامد مع خط آخر ويمر بنقطة معينة مهارة تطبيقية مهمة.

كتابة معادلة خط موازٍ

لإنشاء معادلة خط موازٍ لخط معطى ويمر بنقطة معينة:

1. إيجاد ميل الخط المعطى.
2. استخدام نفس الميل للخط الجديد، لأن الخطوط المتوازية لها نفس الميل.
3. استخدام صيغة الميل ونقطة: (ص ناقص ص1) يساوي م مضروبًا في (س ناقص س1).
   • استخدم الميل الذي وجدته في الخطوة 2 (م).
   • استخدم إحداثيات النقطة المعطاة (س1، ص1) التي يمر بها الخط الجديد.
4. تبسيط المعادلة (اختياري، غالبًا إلى صيغة الميل والمقطع).

مثال: اكتب معادلة الخط الموازي لـ ص = 2 س زائد 3 ويمر بالنقطة (4، 1).

1. ميل الخط المعطى هو م = 2.
2. ميل الخط الجديد سيكون أيضًا 2.
3. باستخدام النقطة (4، 1) والميل 2 في صيغة الميل ونقطة: ص ناقص 1 يساوي 2 مضروبًا في (س ناقص 4)
4. للتبسيط إلى صيغة الميل والمقطع: ص ناقص 1 يساوي 2 س ناقص 8 ص يساوي 2 س ناقص 8 زائد 1 ص يساوي 2 س ناقص 7

كتابة معادلة خط متعامد

لإنشاء معادلة خط متعامد مع خط معطى ويمر بنقطة معينة:

1. إيجاد ميل الخط المعطى (m₁​).
2. حساب ميل الخط المتعامد (m₂​). تذكر أن m₂​ هو المقلوب السالب لـ m₁​. إذا كان m₁​ يساوي رقمًا، فإن m₂​ سيكون سالب واحد مقسومًا على ذلك الرقم.
3. استخدام صيغة الميل ونقطة: (ص ناقص ص1) يساوي م مضروبًا في (س ناقص س1).
   • استخدم m_2​ (ميل الخط المتعامد) كقيمة لـ م.
   • استخدم إحداثيات النقطة المعطاة (س1، ص1) التي يمر بها الخط المتعامد.
4. تبسيط المعادلة (اختياري، غالبًا إلى صيغة الميل والمقطع).

مثال: اكتب معادلة الخط المتعامد مع ص = 3 س زائد 1 ويمر بالنقطة (6، 4).

1. ميل الخط المعطى م1 = 3.
2. ميل الخط المتعامد م2 = سالب 1 مقسومًا على 3.
3. باستخدام النقطة (6، 4) والميل سالب 1 مقسومًا على 3 في صيغة الميل ونقطة: ص ناقص 4 يساوي (سالب 1 مقسومًا على 3) مضروبًا في (س ناقص 6)
4. للتبسيط إلى صيغة الميل والمقطع: ص ناقص 4 يساوي (سالب 1 مقسومًا على 3) س زائد (1 مقسومًا على 3) مضروبًا في 6 ص ناقص 4 يساوي (سالب 1 مقسومًا على 3) س زائد 2 ص يساوي (سالب 1 مقسومًا على 3) س زائد 2 زائد 4 ص يساوي (سالب 1 مقسومًا على 3) س زائد 6

تطبيقات المستقيمات المتوازية والمتعامدة في الحياة العملية

تُعد المستقيمات المتوازية والمتعامدة مفاهيم أساسية في العديد من المجالات:

• الهندسة المعمارية والتشييد: أساس تصميم وبناء الهياكل المستقرة. الجدران المتوازية تضمن المساحة، والجدران المتعامدة مع الأرضية تضمن الاستقرار.
• تخطيط المدن: تصميم شبكات الطرق، حيث تتقاطع الشوارع غالبًا بشكل متوازٍ ومتعامد لتسهيل حركة المرور والتنقل.
• الفيزياء: فهم تحليل المتجهات والقوى. القوى المتعامدة لا تؤثر على بعضها البعض، بينما القوى المتوازية تتجمع. تُستخدم أيضًا في تحليل الحركة.
• النجارة والأعمال اليدوية: استخدام أدوات مثل مربع النجار لضمان زوايا قائمة دقيقة وتصنيع قطع متوازية.
• الرسومات الهندسية وتصميم الكمبيوتر: تُشكل المحاور المتعامدة (س، ص، ع) الأساس لتحديد المواقع ثلاثية الأبعاد، وتُستخدم الخطوط المتوازية لإنشاء منظورات متساوية القياس.
• الملاحة: في الخرائط والملاحة البحرية أو الجوية، تستخدم خطوط الطول (متوازية) وخطوط العرض (متعامدة) لتحديد المواقع بدقة.
• الفن والتصميم: استخدام الخطوط المتوازية والمتعامدة لخلق التوازن، الإيقاع، والمنظور في الأعمال الفنية.
• الرياضيات المتقدمة: تشكل أساسًا لدراسة الفضاءات المتعامدة والمتوازية في الجبر الخطي، والهندسة التحليلية، والتحليل المتجهي.

الخاتمة

تُشكل المستقيمات المتوازية والمستقيمات المتعامدة ركيزتين لا غنى عنهما في بناء الفهم الهندسي والجبري. فبينما تُعبر المستقيمات المتوازية عن الثبات وعدم التقاطع من خلال تساوي ميليهما، تُشير المستقيمات المتعامدة إلى تقاطع فريد بزاوية قائمة، يتميز بميليهما اللذين يكون حاصل ضربهما سالب واحد. إن إتقان هذه المفاهيم، سواء من حيث خصائصها النظرية أو تطبيقاتها العملية، يُعد ضروريًا لتطوير التفكير التحليلي والمكاني. من تصميم الهياكل المعمارية إلى فهم الظواهر الفيزيائية المعقدة، تُقدم المستقيمات المتوازية والمتعامدة إطارًا أساسيًا لوصف العالم من حولنا بدقة، مما يُعزز القدرة على حل المشكلات واتخاذ قرارات مستنيرة في مجالات لا حصر لها.