مقدمة

يُعتبر مفهوما المحيط والمساحة من الأسس الهندسية الهامة التي نتعامل معها في حياتنا اليومية وفي مختلف فروع العلوم والهندسة. يمثل المحيط قياس الطول الكلي للحدود الخارجية لشكل ثنائي الأبعاد، بينما تمثل المساحة قياس الحيز أو السطح الذي يغطيه هذا الشكل. من تحديد طول سياج يحيط بحديقة إلى حساب كمية الطلاء اللازمة لتغطية جدار، ومن تصميم قطع الأراضي إلى تقدير المواد المطلوبة لبناء هيكل، يلعب فهم المحيط والمساحة دورًا حيويًا في حل المشكلات العملية واتخاذ القرارات المستنيرة المتعلقة بالأبعاد والقياسات في عالمنا ثنائي الأبعاد.

يهدف هذا البحث إلى استكشاف مفهومي المحيط والمساحة بعمق، بدءًا من تعريفهما الأساسي وأهميتهما، مرورًا بطرق حسابهما للأشكال الهندسية الأساسية (مثل المربع، المستطيل، المثلث، الدائرة)، وصولًا إلى تطبيقاتهما الواسعة في حياتنا اليومية وفي مختلف المجالات العلمية والهندسية. سيتناول البحث الصيغ الرياضية المستخدمة لحساب المحيط والمساحة لكل شكل من هذه الأشكال، مع توضيح المنطق الهندسي الكامن وراء هذه الصيغ. كما سيسلط الضوء على العلاقة بين المحيط والمساحة وكيف يمكن أن يؤثر تغيير أحدهما على الآخر. إن إتقان مفاهيم المحيط والمساحة يمثل خطوة أساسية في بناء أساس هندسي قوي وتطوير مهارات التفكير المكاني وحل المشكلات العملية المتعلقة بالأبعاد والقياسات.

تعريف المحيط والمساحة وأهميتهما الأساسية

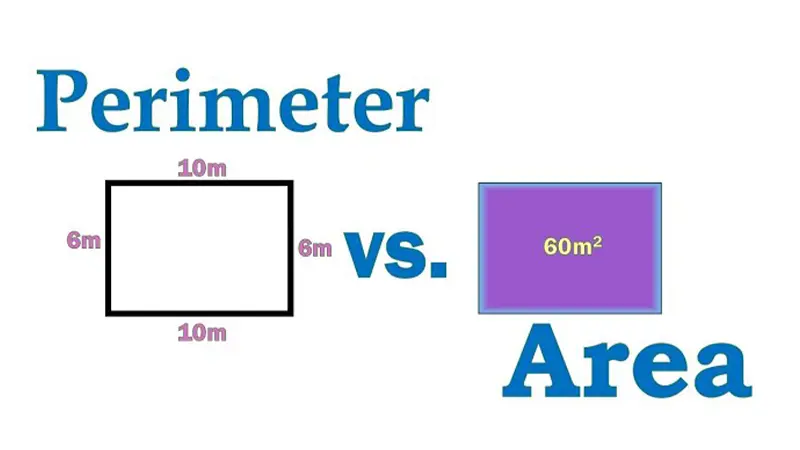
تعريف المحيط (Perimeter): المحيط هو الطول الكلي للحدود الخارجية لشكل ثنائي الأبعاد. يمكن تصوره على أنه المسافة التي تقطعها عند السير حول الحافة الخارجية للشكل. يُقاس المحيط بوحدات الطول مثل السنتيمتر، المتر، البوصة، القدم، وغيرها. لحساب محيط أي مضلع (شكل ذو جوانب مستقيمة)، يتم جمع أطوال جميع أضلاعه.

تعريف المساحة (Area): المساحة هي قياس الحيز أو السطح الذي يغطيه شكل ثنائي الأبعاد. تُقاس المساحة بوحدات مربعة مثل السنتيمتر المربع (cm2)، المتر المربع (m2)، البوصة المربعة (in2)، القدم المربع (ft2)، وغيرها. لحساب مساحة الأشكال المختلفة، تُستخدم صيغ رياضية محددة تعتمد على أبعاد الشكل.

أهميتهما الأساسية:

• القياس والتقدير: يساعدان في قياس وتقدير الأبعاد والكميات المتعلقة بالأشكال ثنائية الأبعاد.
• التخطيط والتصميم: ضروريان في التخطيط والتصميم في مجالات مثل الهندسة المعمارية، والهندسة المدنية، وتصميم الحدائق، وتصميم الأزياء.
• حساب التكاليف: يستخدمان في تقدير تكاليف المواد اللازمة لتغطية أو إحاطة مساحة معينة (مثل تكلفة السياج أو الطلاء أو البلاط).
• فهم العلاقات الهندسية: يساعدان في فهم العلاقات بين أبعاد الأشكال وقياساتها.
• حل المشكلات العملية: يستخدمان في حل العديد من المشكلات العملية المتعلقة بالأبعاد والقياسات في الحياة اليومية والمهنية.

حساب المحيط والمساحة للأشكال الهندسية الأساسية

لكل شكل هندسي أساسي صيغ محددة لحساب محيطه ومساحته:

• المربع (Square): شكل رباعي جميع أضلاعه متساوية الطول (لنفترض طول الضلع s).
  • المحيط: P=s+s+s+s=4s (أربعة أضعاف طول الضلع).
  • المساحة: A=s×s=s2 (طول الضلع مضروبًا في نفسه أو طول الضلع تربيع).
• المستطيل (Rectangle): شكل رباعي كل ضلعين متقابلين متساويين في الطول (لنفترض الطول l والعرض w).
  • المحيط: P=l+w+l+w=2l+2w=2(l+w) (ضعف مجموع الطول والعرض).
  • المساحة: A=l×w (الطول مضروبًا في العرض).
• المثلث (Triangle): شكل ثلاثي له ثلاثة أضلاع (لنفترض أطوال الأضلاع a, b, c) وارتفاع h (العمود النازل من أحد الرؤوس على الضلع المقابل أو امتداده).
  • المحيط: P=a+b+c (مجموع أطوال الأضلاع الثلاثة).
  • المساحة: A=21​×base×height=21​×b×h (نصف طول القاعدة مضروبًا في الارتفاع).
• الدائرة (Circle): شكل منحني مغلق جميع النقاط على محيطه تبعد نفس المسافة عن مركزها (لنفترض نصف القطر r والقطر d=2r). π (باي) هي ثابت رياضي تقريبيًا 3.14159.
  • المحيط (يُسمى أيضًا الطول أو المحيط): C=2πr=πd (ضعف باي مضروبًا في نصف القطر أو باي مضروبًا في القطر).
  • المساحة: A=πr2 (باي مضروبًا في مربع نصف القطر).

العلاقة بين المحيط والمساحة وتأثير تغيير أحدهما على الآخر

لا توجد علاقة ثابتة ومباشرة بين المحيط والمساحة لجميع الأشكال. يمكن لأشكال مختلفة أن يكون لها نفس المحيط ولكن مساحات مختلفة، أو نفس المساحة ولكن محيطات مختلفة.

على سبيل المثال، يمكن لمستطيلين مختلفين أن يكون لهما نفس المحيط ولكن أبعادًا مختلفة وبالتالي مساحات مختلفة. تخيل مستطيلاً أبعاده 10 وحدات و 2 وحدة (المحيط = 24 وحدة، المساحة = 20 وحدة مربعة) ومستطيلاً آخر أبعاده 8 وحدات و 4 وحدات (المحيط = 24 وحدة، المساحة = 32 وحدة مربعة).

وبالمثل، يمكن لأشكال مختلفة أن يكون لها نفس المساحة ولكن محيطات مختلفة. يمكن لمربع مساحته 16 وحدة مربعة (طول الضلع = 4 وحدات، المحيط = 16 وحدة) ومستطيل مساحته 16 وحدة مربعة (أبعاده 8 وحدات و 2 وحدة، المحيط = 20 وحدة).

عند تغيير أبعاد شكل معين، يتأثر كل من محيطه ومساحته، ولكن ليس بالضرورة بنفس النسبة. على سبيل المثال، إذا ضاعفنا طول ضلع مربع، فإن محيطه يتضاعف أيضًا، بينما تتضاعف مساحته أربع مرات.

تطبيقات المحيط والمساحة في الحياة اليومية والمجالات المختلفة

تتعدد تطبيقات المحيط والمساحة في حياتنا اليومية وفي مختلف المجالات:

• البناء والتشييد: حساب كميات مواد البناء (مثل الطوب، البلاط، الدهان)، وتقدير تكاليف الأرض والمساحات المبنية، وتحديد أطوال الأسوار والجدران.
• الزراعة: حساب مساحة الأراضي الزراعية لتحديد كمية البذور والأسمدة المطلوبة، وتقدير إنتاجية المحاصيل.
• تصميم الحدائق: تحديد طول السياج اللازم للحديقة، وحساب مساحة أحواض الزهور والممرات.
• النسيج والخياطة: حساب كمية القماش اللازمة لصنع قطعة ملابس، وتحديد أبعاد القص.
• التعبئة والتغليف: تصميم علب وعبوات بأبعاد ومساحات مناسبة للمنتجات.
• الرياضة: تحديد أبعاد الملاعب والمسارات الرياضية (مثل طول مضمار الجري ومساحة ملعب كرة القدم).
• الخرائط والجغرافيا: حساب المسافات على الخرائط وتقدير مساحات الدول والمناطق.
• التصوير والرسومات: تحديد أبعاد الصور واللوحات وحساب مساحات الألوان.

إن فهم كيفية حساب المحيط والمساحة يمكننا من حل العديد من المشكلات العملية واتخاذ قرارات أفضل في مختلف جوانب حياتنا.

خاتمة

يُعدّ مفهوما المحيط والمساحة أدوات أساسية في الهندسة والرياضيات التطبيقية، حيث يوفران لنا طرقًا لقياس الأبعاد الخارجية والحيز الداخلي للأشكال ثنائية الأبعاد. من خلال فهم تعريفهما وأهميتهما وطرق حسابهما للأشكال الأساسية، نكتسب القدرة على حل المشكلات العملية وتقدير الكميات واتخاذ القرارات المستنيرة في العديد من جوانب حياتنا اليومية وفي مختلف المجالات العلمية والهندسية. إن إتقان حساب المحيط والمساحة ليس مجرد مهارة رياضية، بل هو أساس لفهم أعمق للعالم المكاني من حولنا وتطوير قدراتنا على التفكير الهندسي وحل المشكلات العملية بفعالية.