مقدمة

في عالم الجبر، حيث تصف المعادلات الخطية العلاقات الثابتة بين الكميات، لا توجد صيغة واحدة فقط يمكننا استخدامها لتمثيل هذه العلاقات. فبالإضافة إلى صيغة الميل والمقطع المألوفة، تبرز صيغة الميل ونقطة (Point-Slope Form) كأداة قوية ومرنة لكتابة وتمثيل المعادلات الخطية. هذه الصيغة لا تتطلب معرفة الجزء المقطوع من المحور الصادي مباشرةً، بل تعتمد على أي نقطة معروفة تقع على الخط المستقيم بالإضافة إلى ميله. إن مرونتها تجعلها مفيدة بشكل خاص في السيناريوهات التي يكون فيها الميل ونقطة معينة معروفين، بدلاً من الميل والجزء المقطوع من المحور الصادي. يتيح لنا هذا البحث استكشاف بنية هذه الصيغة، وكيفية استخدامها لكتابة المعادلات، وتمثيلها بيانياً، وتحويلها إلى أشكال أخرى، مما يسهم في تعميق فهمنا لكيفية وصف الخطوط المستقيمة جبرياً وتطبيقاتها المتنوعة في الرياضيات والعلوم.

مراجعة سريعة للمفاهيم الأساسية

لفهم صيغة الميل ونقطة، دعنا نراجع سريعًا بعض المفاهيم الجبرية المرتبطة:

• المعادلة الخطية: هي معادلة جبرية تشكل خطًا مستقيمًا عند تمثيلها بيانيًا. تعرف بأنها خطية لأن أعلى قوة لأي متغير فيها هي واحد (مثلاً، س وليس س تربيع).
• الميل (Slope): هو قياس لانحدار الخط المستقيم واتجاهه. يعرف بأنه نسبة التغير الرأسي (التغير في ص) إلى التغير الأفقي (التغير في س) بين أي نقطتين على الخط. يمكن التفكير فيه كمعدل التغير. يرمز للميل بالحرف م.
  • إذا كان الميل م موجبًا، يتجه الخط للأعلى من اليسار إلى اليمين.
  • إذا كان الميل م سالبًا، يتجه الخط للأسفل من اليسار إلى اليمين.
  • إذا كان الميل م صفرًا، يكون الخط أفقيًا.
  • إذا كان الميل غير معرف (خط رأسي)، فلا يمكن التعبير عنه بهذه الصيغة بشكل مباشر.
• النقطة (Point): أي زوج مرتب (س1، ص1) يمثل إحداثيات نقطة تقع على الخط المستقيم.

صيغة الميل ونقطة: البنية والشرح

تكتب صيغة الميل ونقطة على النحو التالي:

ص ناقص ص1 يساوي م مضروبًا في (س ناقص س1)

دعنا نفكك هذه الصيغة لفهم كل جزء منها:

• ص: يمثل المتغير التابع (المحور الرأسي)، وهو الإحداثي ص لأي نقطة عامة على الخط.
• ص1: يمثل الإحداثي ص للنقطة المعروفة التي تقع على الخط (جزء من النقطة (س1، ص1)).
• م: يمثل الميل للخط المستقيم.
• س: يمثل المتغير المستقل (المحور الأفقي)، وهو الإحداثي س لأي نقطة عامة على الخط.
• س1: يمثل الإحداثي س للنقطة المعروفة التي تقع على الخط (جزء من النقطة (س1، ص1)).

الفكرة الأساسية وراء الصيغة:

تعتمد هذه الصيغة على تعريف الميل. فإذا كان الميل م يساوي (ص ناقص ص1) مقسومًا على (س ناقص س1) (التغير في ص مقسومًا على التغير في س بين نقطة عامة (س، ص) ونقطة معلومة (س1، ص1))، فعند ضرب الطرفين في (س ناقص س1)، نحصل على م مضروبًا في (س ناقص س1) يساوي ص ناقص ص1. ومن ثم، يمكننا إعادة ترتيبها لتصبح ص ناقص ص1 يساوي م مضروبًا في (س ناقص س1).

هذا يعني أنك إذا عرفت ميل الخط المستقيم م وإحداثيات نقطة واحدة فقط (س1، ص1) تقع على هذا الخط، يمكنك كتابة معادلته مباشرةً باستخدام هذه الصيغة.

كيفية كتابة معادلة خطية بصيغة الميل ونقطة

تعد هذه العملية مباشرة بمجرد فهم بنية الصيغة.

الخطوات:

1. تحديد الميل (م): يجب أن تكون قيمة الميل معروفة.
   • قد تعطى لك مباشرة.
   • قد تضطر لحسابها من نقطتين باستخدام صيغة الميل: م يساوي (ص2 ناقص ص1) مقسومًا على (س2 ناقص س1).
2. تحديد نقطة واحدة على الخط (س1، ص1): يجب أن تكون إحداثيات نقطة واحدة على الأقل معروفة.
   • قد تعطى لك مباشرة.
   • إذا أعطيت نقطتين، يمكنك اختيار أي واحدة منهما لاستخدامها في الصيغة.
3. التعويض في الصيغة: استبدل قيم م، س1، و ص1 في صيغة الميل ونقطة: ص ناقص ص1 يساوي م مضروبًا في (س ناقص س1).

مثال 1: إعطاء الميل ونقطة

اكتب معادلة الخط المستقيم الذي ميله 3 ويمر بالنقطة (4، 5).

1. الميل م = 3.
2. النقطة (س1، ص1) = (4، 5).
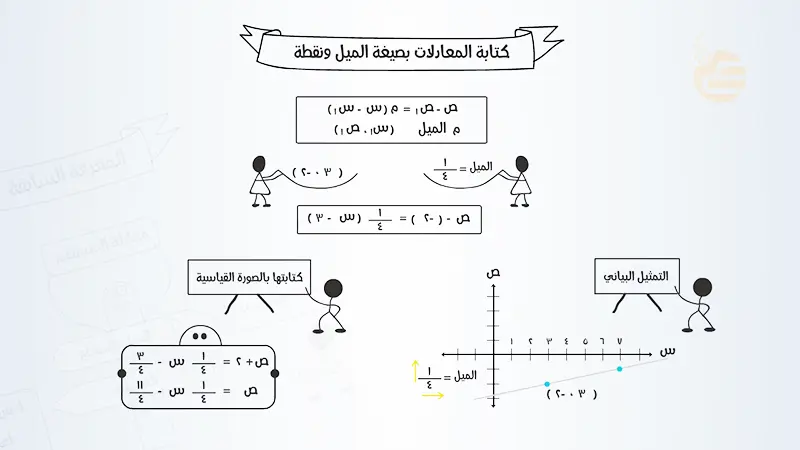
3. التعويض في الصيغة: ص ناقص 5 يساوي 3 مضروبًا في (س ناقص 4) هذه هي المعادلة بصيغة الميل ونقطة.

مثال 2: إعطاء نقطتين

اكتب معادلة الخط المستقيم الذي يمر بالنقطتين (2، 1) و (6، 9).

1. حساب الميل (م): م يساوي (9 ناقص 1) مقسومًا على (6 ناقص 2) م يساوي 8 مقسومًا على 4 م يساوي 2
2. اختيار نقطة: يمكننا اختيار أي من النقطتين. لنختر النقطة (2، 1) لتكون (س1، ص1).
3. التعويض في الصيغة: ص ناقص 1 يساوي 2 مضروبًا في (س ناقص 2) هذه هي المعادلة بصيغة الميل ونقطة. (لو اخترنا النقطة (6، 9) لكانت المعادلة ص ناقص 9 يساوي 2 مضروبًا في (س ناقص 6)، وهي معادلة مكافئة).

تحويل صيغة الميل ونقطة إلى صيغة الميل والمقطع

في كثير من الأحيان، بعد كتابة المعادلة بصيغة الميل ونقطة، قد تحتاج إلى تحويلها إلى صيغة الميل والمقطع (ص = م س زائد ب) لأنها أكثر شيوعًا لبعض التطبيقات (مثل تمثيلها بيانيًا باستخدام الجزء المقطوع من المحور الصادي).

الخطوات:

1. ابدأ بمعادلة بصيغة الميل ونقطة: ص ناقص ص1 يساوي م مضروبًا في (س ناقص س1).
2. وزع الميل (م) على القوس: اضرب م في كل حد داخل القوس (س ناقص س1). يصبح: ص ناقص ص1 يساوي م س ناقص م س1
3. عزل ص: أضف ص1 إلى كلا طرفي المعادلة. يصبح: ص يساوي م س ناقص م س1 زائد ص1

الآن، المعادلة في صيغة الميل والمقطع، حيث الميل هو م والجزء المقطوع من المحور الصادي هو (ناقص م س1 زائد ص1).

مثال: حول المعادلة ص ناقص 5 يساوي 3 مضروبًا في (س ناقص 4) إلى صيغة الميل والمقطع.

1. وزع الميل (3): ص ناقص 5 يساوي 3س ناقص 12
2. أضف 5 إلى كلا الطرفين: ص يساوي 3س ناقص 12 زائد 5 ص يساوي 3س ناقص 7

الآن، المعادلة بصيغة الميل والمقطع، حيث الميل م = 3 والجزء المقطوع من المحور الصادي ب = -7.

تمثيل المعادلات المكتوبة بصيغة الميل ونقطة بيانياً

على الرغم من أن صيغة الميل ونقطة لا تعطي الجزء المقطوع من المحور الصادي مباشرة، إلا أنها لا تزال سهلة الرسم بيانيًا.

الخطوات:

1. تحديد ورسم النقطة المعروفة (س1، ص1):
   • ابحث عن قيم س1 و ص1 في المعادلة ص ناقص ص1 يساوي م مضروبًا في (س ناقص س1).
   • قم برسم هذه النقطة على المستوى الإحداثي الديكارتي.
2. تحديد الميل (م) واستخدامه لإيجاد نقطة ثانية:
   • تذكر أن الميل هو “التغير في ص مقسومًا على التغير في س”.
   • إذا كان الميل عددًا صحيحًا، اكتبه ككسر بوضع 1 في المقام.
   • من النقطة (س1، ص1) التي رسمتها في الخطوة 1:
     • تحرك عموديًا للأعلى أو للأسفل (حسب إشارة البسط في الميل).
     • ثم تحرك أفقيًا لليمين أو لليسار (حسب إشارة المقام في الميل، غالبًا لليمين).
   • قم برسم النقطة الثانية التي توصلت إليها.
3. رسم الخط المستقيم:
   • باستخدام مسطرة، ارسم خطًا مستقيمًا يمر عبر النقطتين اللتين رسمتهما.
   • مد الخط في كلا الاتجاهين مع وضع أسهم عند الأطراف، للإشارة إلى أنه يمتد إلى ما لا نهاية.

مثال: مثل بيانياً المعادلة ص ناقص 2 يساوي سالب 1 مضروبًا في (س زائد 3). (لاحظ أن س زائد 3 تعني س ناقص سالب 3، لذا س1 = سالب 3).

1. النقطة المعروفة (س1، ص1): من المعادلة، ص1 = 2 و س1 = سالب 3. ارسم النقطة (سالب 3، 2).
2. الميل (م): م = سالب 1. يمكن كتابته كسالب 1 مقسومًا على 1.
   • من النقطة (سالب 3، 2): تحرك وحدة واحدة للأسفل (التغير في ص).
   • ثم تحرك وحدة واحدة لليمين (التغير في س).
   • ستصل إلى النقطة (سالب 2، 1). ارسم هذه النقطة.
3. رسم الخط: ارسم خطًا مستقيمًا يمر بالنقطتين (سالب 3، 2) و (سالب 2، 1).

متى نستخدم صيغة الميل ونقطة

تعد صيغة الميل ونقطة مفيدة بشكل خاص في السيناريوهات التالية:

1. عندما يعطى الميل ونقطة معينة: هذه هي الحالة الأكثر وضوحًا لاستخدامها، حيث يمكنك التعويض مباشرة في الصيغة.
2. عندما يعطى نقطتان فقط: يمكنك أولاً حساب الميل من النقطتين، ثم استخدام الميل وإحدى النقطتين لكتابة المعادلة بصيغة الميل ونقطة. هذه الطريقة غالبًا ما تكون أسهل من محاولة حساب الجزء المقطوع من المحور الصادي أولاً.
3. في تطبيقات معينة: قد تكون بعض المشكلات الواقعية تقدم الميل ونقطة بداية (ليست بالضرورة الجزء المقطوع من المحور الصادي)، مما يجعل هذه الصيغة الخيار الأمثل.
   • مثال: إذا عرفت أن تكلفة خدمة معينة تزداد بمعدل 10 دنانير لكل ساعة (الميل) وأنك دفعت 50 دينارًا مقابل 3 ساعات عمل (النقطة)، يمكنك كتابة المعادلة مباشرة.

الخاتمة

تعد صيغة الميل ونقطة أداة أساسية ومرنة في ترسانة الجبر، تمكننا من بناء معادلات الخطوط المستقيمة حتى عندما لا يكون الجزء المقطوع من المحور الصادي معروفًا مباشرة. من خلال فهم بنيتها التي تستند إلى مفهوم الميل ونقطة واحدة معلومة، يمكن للطلاب كتابة المعادلات بسهولة، وتحويلها إلى صيغة الميل والمقطع عند الحاجة، وتمثيلها بيانياً بدقة. إن هذه المرونة تجعلها ضرورية في حل مجموعة واسعة من المشكلات الرياضية والتطبيقية، حيث تقدم نقطة انطلاق قوية لوصف العلاقات الخطية في سياقات متنوعة. تعزز صيغة الميل ونقطة فهمنا العميق للطبيعة الخطية للعلاقات الكمية، وتسهم في بناء أساس رياضي متين للتعامل مع تحديات أكثر تعقيدًا في المستقبل.