مقدمة

تُعد الأشكال الرباعية (Quadrilaterals) من المفاهيم الأساسية في علم الهندسة المستوية، فهي تمثل مضلعات مغلقة تتكون من أربعة أضلاع وأربع زوايا وأربعة رؤوس. تشكل هذه الأشكال المتنوعة أساسًا لفهم العديد من المفاهيم الهندسية الأكثر تعقيدًا وتظهر في العديد من التطبيقات العملية في حياتنا اليومية، من تصميم المباني والأثاث إلى فهم الخرائط والرسومات التقنية. يتميز كل نوع من الأشكال الرباعية بخصائص فريدة تتعلق بأطوال أضلاعه وقياسات زواياه وعلاقات التوازي والتعامد بين أضلاعه، مما يجعل دراستها ضرورية لبناء أساس قوي في علم الهندسة.

تتنوع الأشكال الرباعية بشكل كبير، بدءًا من الأشكال غير المنتظمة التي لا تملك أي خصائص مميزة، وصولًا إلى الأشكال المنتظمة مثل المربع الذي يتمتع بأعلى درجة من التماثل. بين هذين الطرفين، نجد أنواعًا أخرى مثل المستطيل والمعين وشبه المنحرف ومتوازي الأضلاع، ولكل منها مجموعة محددة من الخصائص التي تميزه عن غيره. إن فهم هذه التصنيفات والخصائص يمكّننا من التعرف على الأشكال الرباعية المختلفة وتطبيق قواعدها في حل المسائل الهندسية واستنتاج العلاقات بينها.

يهدف هذا البحث إلى استكشاف عالم الأشكال الرباعية بعمق، وتوضيح تعريفها وخصائصها العامة، واستعراض أنواعها المختلفة وتصنيفاتها، بالإضافة إلى بيان أهميتها وتطبيقاتها في حل المسائل الهندسية وفهم العالم من حولنا. سنسعى لتقديم صورة شاملة لهذه الأشكال الأساسية التي تشكل جزءًا هامًا من دراسة الهندسة المستوية.

تعريف وخصائص الأشكال الرباعية العامة

الشكل الرباعي هو مضلع له أربعة أضلاع وأربع زوايا وأربعة رؤوس.

• الخصائص العامة:
  • يتكون من أربعة أضلاع مستقيمة تصل بين أربعة رؤوس مختلفة تقع في نفس المستوى.
  • له أربع زوايا داخلية.
  • مجموع قياسات زواياه الداخلية يساوي 360 درجة.
  • له قطران يصلان بين الرؤوس غير المتجاورة.

أنواع الأشكال الرباعية وتصنيفاتها

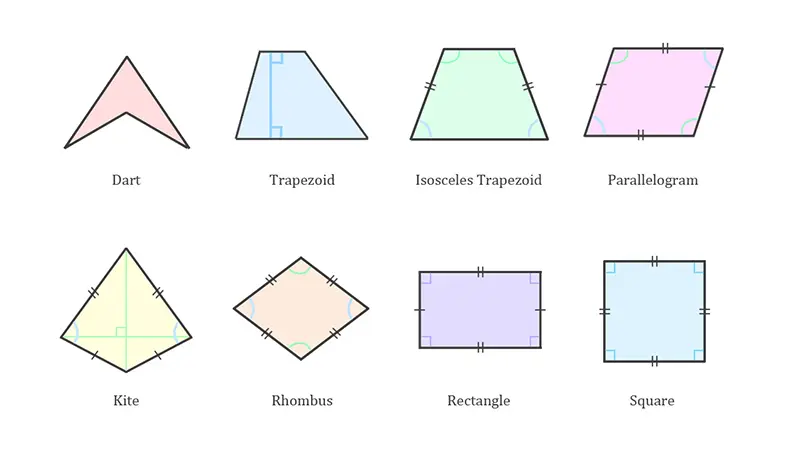
يمكن تصنيف الأشكال الرباعية إلى عدة أنواع بناءً على خصائص أضلاعها وزواياها:

• متوازي الأضلاع: هو شكل رباعي فيه كل ضلعين متقابلين متوازيين ومتساويين في الطول.
  • الخصائص الإضافية:
    • كل زاويتين متقابلتين متساويتين في القياس.
    • كل زاويتين متجاورتين متكاملتين (مجموع قياسيهما 180 درجة).
    • قطراه ينصف كل منهما الآخر.
• المستطيل: هو متوازي أضلاع جميع زواياه قائمة (90 درجة).
  • الخصائص الإضافية:
    • جميع خصائص متوازي الأضلاع تنطبق عليه.
    • قطراه متساويان في الطول.
• المعين: هو متوازي أضلاع جميع أضلاعه متساوية في الطول.
  • الخصائص الإضافية:
    • جميع خصائص متوازي الأضلاع تنطبق عليه.
    • قطراه متعامدان وينصفان زواياه.
• المربع: هو مستطيل جميع أضلاعه متساوية في الطول (أو هو معين جميع زواياه قائمة). يعتبر الشكل الرباعي المنتظم.
  • الخصائص الإضافية:
    • جميع خصائص المستطيل والمعين تنطبق عليه.
    • أضلاعه الأربعة متساوية في الطول.
    • زواياه الأربعة قائمة.
    • قطراه متساويان في الطول ومتعامدان وينصفان زواياه.
• شبه المنحرف: هو شكل رباعي فيه ضلعان فقط متقابلان متوازيان.
  • الخصائص الإضافية (لأنواع خاصة):
    • شبه المنحرف متساوي الساقين: فيه الساقان غير المتوازيين متساويان في الطول، وزوايا القاعدة متساوية.
    • شبه المنحرف القائم الزاوية: فيه زاويتان قائمتان.
• شبه المنحرف العام: فيه ضلعان فقط متقابلان متوازيان وليس له خصائص إضافية.
• الشكل الرباعي العام: هو شكل رباعي لا تتوفر فيه أي من خصائص التوازي أو تساوي الأضلاع أو الزوايا الخاصة.
• الطائرة الورقية (Kite): هو شكل رباعي فيه زوجان متجاوران من الأضلاع متساويان في الطول.
  • الخصائص الإضافية:
    • قطراه متعامدان.
    • أحد القطرين ينصف القطر الآخر وينصف الزاويتين الواقعتين على طرفيه.
    • زاويتان فقط متقابلتان متساويتان في القياس (الزاويتان بين الضلعين غير المتساويين).

العلاقات بين أنواع الأشكال الرباعية

توجد علاقات هرمية بين أنواع الأشكال الرباعية:

• المربع هو نوع خاص من المستطيل (بأضلاع متساوية) وهو أيضًا نوع خاص من المعين (بزوايا قائمة).
• المستطيل والمعين هما نوعان خاصان من متوازي الأضلاع (بزوايا قائمة وأضلاع متساوية على التوالي).
• متوازي الأضلاع هو نوع خاص من شبه المنحرف (فيه زوجان من الأضلاع المتوازية).
• كل من متوازي الأضلاع والمستطيل والمعين والمربع والطائرة الورقية وشبه المنحرف هي أشكال رباعية.

خصائص الأضلاع والزوايا والأقطار في الأشكال الرباعية

• الأضلاع: يمكن أن تكون متساوية في الطول أو مختلفة، متوازية أو غير متوازية.
• الزوايا: يمكن أن تكون قائمة أو حادة أو منفرجة، وقد تكون متساوية أو مختلفة. مجموع الزوايا الداخلية دائمًا 360 درجة.
• الأقطار: تصل بين الرؤوس غير المتجاورة، وقد تكون متساوية في الطول أو مختلفة، وقد تنصف بعضها البعض أو تكون متعامدة.

تطبيقات الأشكال الرباعية في الحياة العملية

تظهر الأشكال الرباعية في العديد من التطبيقات العملية:

• الهندسة المعمارية والبناء: تصميم الغرف والمباني والواجهات يعتمد على الأشكال الرباعية مثل المستطيلات والمربعات.
• التصميم الصناعي: تصميم المنتجات والأجزاء غالبًا ما يتضمن أشكالًا رباعية.
• الخرائط والمسح: تمثيل الأراضي والمناطق يعتمد على تقسيمها إلى أشكال رباعية.
• الأثاث: تصميم الطاولات والكراسي وغيرها يعتمد على الأشكال الرباعية.
• الفنون والتصميم الجرافيكي: استخدام الأشكال الرباعية في التكوينات الفنية والتصاميم.
• الرياضيات والعلوم: فهم العلاقات الهندسية وحل المسائل يعتمد على معرفة خصائص الأشكال الرباعية.
• التكنولوجيا: تصميم شاشات العرض ولوحات المفاتيح وغيرها يعتمد على الأشكال الرباعية.

كيفية تحديد نوع الشكل الرباعي

لتحديد نوع شكل رباعي معين، يمكن اتباع الخطوات التالية:

1. فحص الأضلاع: هل هناك أضلاع متوازية؟ هل هناك أضلاع متساوية في الطول؟
2. فحص الزوايا: هل هناك زوايا قائمة؟ هل هناك زوايا متساوية في القياس؟
3. فحص الأقطار: هل الأقطار متساوية في الطول؟ هل تنصف بعضها البعض؟ هل هي متعامدة؟

من خلال الإجابة على هذه الأسئلة ومقارنة الخصائص بالشروط المميزة لكل نوع من الأشكال الرباعية، يمكن تحديد نوع الشكل بدقة.

الخاتمة

في الختام، تتجلى لنا أهمية الأشكال الرباعية وتنوعها في علم الهندسة وتطبيقاتها العملية. من متوازي الأضلاع بفروعه المختلفة (المستطيل والمعين والمربع) إلى شبه المنحرف والطائرة الورقية والشكل الرباعي العام، يتميز كل نوع بخصائص فريدة تحدد شكله وسلوكه الهندسي. إن فهم هذه التصنيفات والخصائص والعلاقات بينها يمكّننا من تحليل الأشكال الهندسية وحل المسائل المعقدة وتفسير العالم من حولنا بطريقة أكثر دقة وعمقًا. فالأشكال الرباعية ليست مجرد مفاهيم نظرية، بل هي لبنات أساسية في بناء الفهم الهندسي وتطبيقاته الواسعة في حياتنا اليومية.