مقدمة

في عالمنا المليء بالحركة والتغير، تتجلى أهمية فهم كيفية تغير الكميات بعضها بالنسبة لبعض. في الرياضيات، يقدم مفهوم معدل التغير (Rate of Change) و الميل (Slope) الأدوات الأساسية لتحليل هذه الديناميكية. فبينما يشير معدل التغير إلى سرعة أو مدى تغير متغير واحد بالنسبة لمتغير آخر، يعتبر الميل التجسيد البياني لهذا المعدل، موضحًا انحدار الخط المستقيم الذي يمثل العلاقة. يعد هذان المفهومان حجر الزاوية في فهم الدوال الخطية، وهما لا يقتصران على المعادلات الجبرية المجردة فحسب، بل يمتدان إلى تطبيقات واسعة في الفيزياء، الاقتصاد، الهندسة، وحتى في تحليل الظواهر اليومية. إن استيعاب العلاقة الجوهرية بين معدل التغير والميل، وكيفية حسابهما وتفسيرهما، يعد مفتاحًا أساسيًا لفك شفرة العلاقات المتغيرة وبناء نماذج رياضية دقيقة للعالم من حولنا.

مفهوم معدل التغير

معدل التغير (Rate of Change) هو مقياس يحدد مدى تغير كمية ما (المتغير التابع) بالنسبة لتغير كمية أخرى (المتغير المستقل). ببساطة، يوضح كم يزيد أو ينقص المتغير التابع عندما يتغير المتغير المستقل بوحدة واحدة.

التعريف الرياضي: يعرف معدل التغير عادة كنسبة بين التغير في المتغير التابع والتغير في المتغير المستقل. يرمز له غالبًا بالحرف اليوناني دلتا (Δ) التي تعني “التغير في”. يمكننا القول أن معدل التغير يساوي التغير في المتغير التابع مقسومًا على التغير في المتغير المستقل. إذا كانت لدينا نقطتان (المدخل الأول، المخرج الأول) و (المدخل الثاني، المخرج الثاني)، فإن معدل التغير يحسب كالتالي: (المخرج الثاني ناقص المخرج الأول) مقسومًا على (المدخل الثاني ناقص المدخل الأول).

أنواع معدل التغير:

• معدل التغير الثابت (Constant Rate of Change): يحدث عندما تتغير الكمية بنفس المقدار لكل وحدة تغير في الكمية الأخرى. هذا النوع هو سمة الدوال الخطية، حيث يكون الميل ثابتًا.
• معدل التغير المتغير (Variable Rate of Change): يحدث عندما تتغير الكمية بمقادير مختلفة لكل وحدة تغير في الكمية الأخرى. هذا النوع يميز الدوال غير الخطية (المنحنيات)، حيث يتغير الميل من نقطة لأخرى، وهو ما يدرس في فروع الرياضيات المتقدمة مثل التفاضل.

وحدات القياس: وحدة قياس معدل التغير هي دائمًا وحدة المتغير التابع مقسومة على وحدة المتغير المستقل. مثال: إذا كانت المسافة تقاس بالأمتار والزمن بالثواني، فإن معدل التغير (السرعة) يقاس بالمتر لكل ثانية.

مفهوم الميل

الميل (Slope) هو مقياس انحدار الخط المستقيم واتجاهه في المستوى الإحداثي الديكارتي. إنه يقدم وصفًا بصريًا لمعدل التغير الثابت في الدالة الخطية.

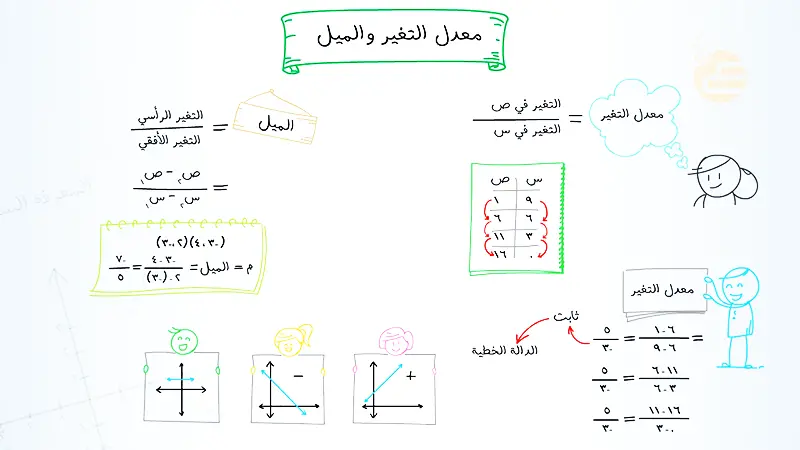
التعريف الرياضي: يعرف الميل بأنه “الارتفاع على المسافة الأفقية”، وهو يمثل نسبة التغير الرأسي إلى التغير الأفقي بين أي نقطتين على الخط. يمكننا التفكير في الميل كعدد الوحدات التي يتغير بها الخط رأسيًا لكل وحدة يتغيرها أفقيًا. صيغة حساب الميل (m) هي: التغير الرأسي مقسومًا على التغير الأفقي. أو، إذا كانت لدينا نقطتان (س1، ص1) و (س2، ص2)، فإن الميل يساوي (ص2 ناقص ص1) مقسومًا على (س2 ناقص س1).

أنواع الميل واتجاه الخط:

1. الميل الموجب (m > 0): الخط يتجه للأعلى من اليسار إلى اليمين. يشير إلى علاقة طردية بين المدخلات والمخرجات (كلما زادت المدخلات، زادت المخرجات).
2. الميل السالب (m < 0): الخط يتجه للأسفل من اليسار إلى اليمين. يشير إلى علاقة عكسية بين المدخلات والمخرجات (كلما زادت المدخلات، قلت المخرجات).
3. الميل الصفري (m = 0): الخط يكون أفقيًا. يشير إلى أن قيمة المخرجات ثابتة بغض النظر عن تغير المدخلات. في هذه الحالة، يكون الخط مستقيمًا وموازيًا للمحور الأفقي.
4. الميل غير المعرف (Undefined Slope): الخط يكون رأسيًا. يحدث عندما يكون التغير الأفقي صفرًا (أي أن المدخلات لا تتغير بين نقطتين مختلفتين على الخط)، مما يعني أن القسمة على صفر، وهو أمر غير ممكن رياضيًا. في هذه الحالة، يكون الخط مستقيمًا وموازيًا للمحور الرأسي.

صيغة الميل والمقطع: المعادلة الخطية في صيغة الميل والمقطع هي: ص = م س + ب. هذه الصيغة توضح مباشرة الميل (م) والجزء المقطوع من المحور الصادي (ب).

• م: هو الميل.
• ب: هو الجزء المقطوع من المحور الصادي (النقطة التي يقطع فيها الخط المحور الصادي، وهي دائمًا النقطة (0، ب)).

العلاقة بين معدل التغير والميل

في سياق الدوال الخطية، الميل هو نفسه معدل التغير الثابت. أي أن مفهومي الميل ومعدل التغير يستخدمان بالتبادل لوصف انحدار الخط المستقيم وكيفية تغير المتغير التابع بالنسبة للمتغير المستقل.

التكامل والتوضيح:

• عندما نتحدث عن معدل التغير، فإننا نركز على الكمية أو السرعة التي يتغير بها شيء ما في سياق معين (مثال: سرعة السيارة، معدل نمو السكان).
• عندما نتحدث عن الميل، فإننا نركز على التمثيل البياني لهذا التغير، أي الانحدار البصري للخط على الرسم البياني.
• إذا كان الرسم البياني للعلاقة بين متغيرين خطًا مستقيمًا، فهذا يعني أن معدل التغير ثابت، وقيمته هي قيمة الميل.

أمثلة لترسيخ الفهم:

• معدل نمو نبات: إذا نما نبات 5 سنتيمترات كل يوم، فإن معدل التغير هو 5 سنتيمترات لكل يوم. إذا رسمت علاقة طول النبات بالزمن، فإن ميل الخط سيكون 5.
• سرعة سيارة: إذا قطعت سيارة مسافة 100 كيلومتر في ساعتين، فإن معدل تغير المسافة بالنسبة للزمن (السرعة) هو 50 كيلومترًا لكل ساعة. على الرسم البياني للمسافة مقابل الزمن، سيكون ميل الخط 50.

حساب معدل التغير والميل (أمثلة عملية)

مثال 1: حساب الميل من نقطتين:

أوجد ميل الخط المستقيم الذي يمر بالنقطتين (2, 3) و (5, 9).

1. حدد إحداثيات النقاط:
   • النقطة الأولى (س1، ص1) = (2، 3)
   • النقطة الثانية (س2، ص2) = (5، 9)
2. طبق صيغة الميل:
   • التغير في ص = ص2 ناقص ص1 = 9 ناقص 3 = 6
   • التغير في س = س2 ناقص س1 = 5 ناقص 2 = 3
   • الميل = التغير في ص مقسومًا على التغير في س = 6 مقسومًا على 3 = 2 الميل هو 2. هذا يعني أن قيمة ص تزداد بمقدار 2 لكل وحدة زيادة في س.

مثال 2: حساب معدل التغير من معادلة خطية:

إذا كانت لدينا المعادلة: ص = 4س + 10. أوجد معدل التغير لهذه الدالة.

• هذه المعادلة مكتوبة في صيغة الميل والمقطع (ص = م س + ب).
• بالمقارنة، نجد أن قيمة الميل (م) هي 4.
• إذن، معدل التغير هو 4. هذا يعني أن قيمة ص تزداد بمقدار 4 وحدات لكل وحدة زيادة في س.

مثال 3: تحديد الميل من معادلة في صيغة الميل والمقطع:

حدد الميل للمعادلة ص = -3س + 7.

• المعادلة مكتوبة بالفعل في صيغة الميل والمقطع (ص = م س + ب).
• بالمقارنة، نجد أن قيمة م (الميل) هي -3.
• الميل هو -3. هذا يعني أن الخط يتجه للأسفل من اليسار إلى اليمين، وأن ص تتناقص بمقدار 3 لكل وحدة زيادة في س.

تطبيقات معدل التغير والميل في الحياة الواقعية

تستخدم مفاهيم معدل التغير والميل بشكل واسع في العديد من المجالات:

الفيزياء:

• السرعة: هي معدل تغير المسافة بالنسبة للزمن. ميل منحنى المسافة-الزمن يمثل السرعة. إذا تحرك جسم مسافة 20 مترًا في 5 ثوانٍ، فإن سرعته 4 أمتار في الثانية.
• التسارع: هو معدل تغير السرعة بالنسبة للزمن. ميل منحنى السرعة-الزمن يمثل التسارع.
• القوة: في قانون هوك، القوة المؤثرة على زنبرك تتناسب طرديًا مع إزاحته، والميل يمثل ثابت الزنبرك.

الاقتصاد والأعمال:

• التضخم: معدل تغير أسعار السلع والخدمات بمرور الوقت. إذا ارتفعت أسعار السلع بنسبة 5% في عام، فإن معدل التضخم هو 5% سنويًا.
• النمو الاقتصادي: معدل تغير الناتج المحلي الإجمالي.
• التكلفة الحدية: معدل تغير التكلفة الإجمالية لإنتاج وحدة إضافية واحدة.
• الإيرادات الحدية: معدل تغير الإيرادات الكلية من بيع وحدة إضافية واحدة.
• تحليل المبيعات والأرباح: يمكن حساب معدل التغير في المبيعات لتحديد الاتجاهات والتنبؤ بالمستقبل.

الهندسة:

• تصميم الطرق والمنحدرات: يستخدم الميل لتحديد انحدار الطرق والمنحدرات لضمان السلامة والكفاءة. على سبيل المثال، قد يتطلب قانون البناء أن يكون ميل المنحدر 1 على 12، مما يعني ارتفاع وحدة واحدة لكل 12 وحدة أفقية.
• تحليل ميل السقوف: في الهندسة المعمارية، يحدد الميل كيفية تصريف المياه من الأسطح.

العلوم البيولوجية:

• معدل نمو الكائنات الحية: كم يزداد وزن أو طول كائن حي بمرور الوقت. يمكن تتبع نمو طفل بمعدل معين من السنتيمترات شهريًا.
• معدل انتشار الأمراض: كيفية تغير عدد المصابين بمرور الوقت، وهو أمر حيوي في علم الأوبئة.

الإحصاء وتحليل البيانات:

• يستخدم الميل في تحليل الانحدار الخطي لتحديد قوة واتجاه العلاقة بين متغيرين.
• فهم الاتجاهات في البيانات الزمنية (مثل أسعار الأسهم، درجات الحرارة).

الحياة اليومية:

• استهلاك الوقود: معدل استهلاك السيارة للوقود لكل كيلومتر. على سبيل المثال، 10 كيلومترات لكل لتر.
• معدل ضربات القلب: عدد ضربات القلب في الدقيقة.
• فواتير الخدمات: معدل استهلاك الكهرباء أو المياه بمرور الوقت.

الخاتمة

يشكل مفهوما معدل التغير والميل ركيزتين أساسيتين في فهم ديناميكية العلاقات بين الكميات في الرياضيات وفي العالم الحقيقي. فمن خلال قدرتهما على قياس انحدار الخط المستقيم وتحديد سرعة التغير، يقدمان لنا أدوات تحليلية قوية. إن فهم العلاقة الجوهرية بين الميل ومعدل التغير الثابت في الدوال الخطية يفتح الأبواب أمام تطبيقات لا حصر لها، من تحليل البيانات الاقتصادية وتصميم الهياكل الهندسية إلى فهم الظواهر الطبيعية والتنبؤ بسلوكها. إن إتقان كيفية حساب وتفسير هذين المفهومين لا يعزز المهارات الرياضية فحسب، بل ينمي أيضًا التفكير النقدي والقدرة على تحليل العلاقات المتغيرة في سياقات متنوعة، مما يجعلهما أدوات لا غنى عنها في أي مجال يتطلب الفهم الكمي والتنبؤ.