مقدمة

في جوهر الرياضيات، لا تُعد الأعداد والعمليات مجرد كيانات منعزلة، بل هي جزء من شبكة واسعة من العلاقات التي تربط بينها وتُحدد سلوكها. فمنذ المراحل الأولى لتعلم الرياضيات، يبدأ الطلاب في استكشاف هذه العلاقات، بدءًا من العلاقة بين الأعداد في عمليات الجمع والطرح، وصولًا إلى العلاقات المعقدة بين المتغيرات في المعادلات والمتباينات، ودراسة الدوال التي تُعد تجسيدًا للعلاقات الخاصة. إن مفهوم العلاقة هو مفهوم أساسي يُمكننا من فهم كيفية ترابط العناصر في مجموعات مختلفة، وكيف يُمكننا وصف هذه الروابط بطرق رياضية دقيقة. تُقدم العلاقات إطارًا لتنظيم المعلومات، وتحليل الأنماط، وبناء التنبؤات، وهي بذلك تُشكل اللبنة الأساسية ليس فقط في الجبر والهندسة، بل في مجالات أوسع مثل المنطق وعلوم الحاسوب. إن استيعاب طبيعة العلاقات وأنواعها وخصائصها يُعد خطوة حاسمة نحو بناء فهم رياضي أعمق وأكثر شمولًا.

تعريف العلاقة في الرياضيات

في الرياضيات، تُعرف العلاقة بأنها مجموعة من الأزواج المرتبة التي تربط عناصر من مجموعة (تُسمى المجال) بعناصر من مجموعة أخرى (تُسمى المدى). ببساطة، تُحدد العلاقة كيفية ارتباط عنصر من المجموعة الأولى بعنصر من المجموعة الثانية.

• الزوج المرتب (Ordered Pair): هو زوج من العناصر، يُرمز له بالصورة (a,b)، حيث a هو العنصر الأول (من المجال) و b هو العنصر الثاني (من المدى). الترتيب هنا مهم، فـ (a,b) ليس بالضرورة هو نفسه (b,a).
• المجال (Domain): هو مجموعة كل العناصر الأولى في الأزواج المرتبة التي تُكون العلاقة. بعبارة أخرى، هي مجموعة المدخلات المحتملة للعلاقة.
• المدى (Range): هو مجموعة كل العناصر الثانية في الأزواج المرتبة التي تُكون العلاقة. بعبارة أخرى، هي مجموعة المخرجات المحتملة للعلاقة.

مثال بسيط: لنفترض أن لدينا مجموعتين: المجموعة A (أسماء طلاب): {علي، سارة، أحمد} المجموعة B (مواد دراسية): {رياضيات، علوم، تاريخ}

يمكننا تعريف علاقة “يُحب دراسة” بين الطلاب والمواد: R = {(علي, رياضيات), (سارة, علوم), (أحمد, رياضيات), (سارة, تاريخ)}

• المجال: {علي، سارة، أحمد}
• المدى: {رياضيات، علوم، تاريخ}

طرق تمثيل العلاقات

يمكن تمثيل العلاقات في الرياضيات بعدة طرق، كل منها يُبرز جانبًا مختلفًا من العلاقة:

1. قائمة الأزواج المرتبة: وهي الطريقة الأكثر مباشرة، حيث تُسرد جميع الأزواج المرتبة التي تُشكل العلاقة. مثال: R = {(1, 2), (2, 4), (3, 6)}
2. الجدول: تُمكننا الجداول من تنظيم الأزواج المرتبة في عمودين، أحدهما للمجال والآخر للمدى.

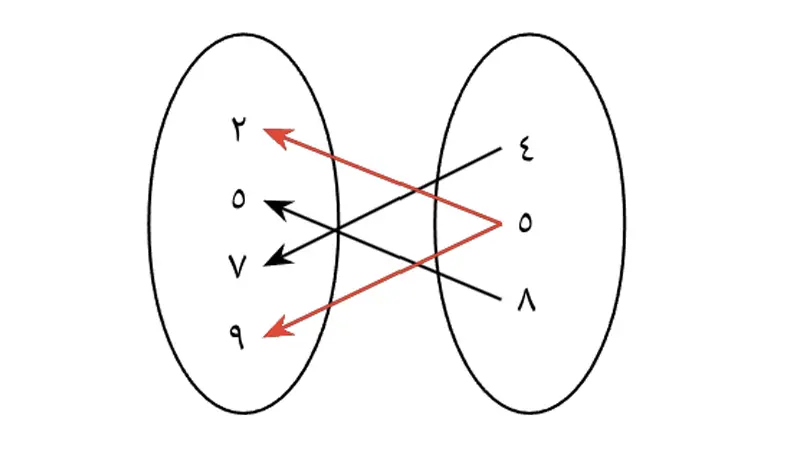
3. المخطط السهمي (Arrow Diagram): يُرسم دائرتان أو شكلان بيضاويان يُمثلان المجموعتين (المجال والمدى)، وتُرسم أسهم من عناصر المجال إلى عناصر المدى التي ترتبط بها.
   • (تصور دائرة للمجال تحتوي على 1, 2, 3 ودائرة للمدى تحتوي على 2, 4, 6، وأسهم من 1 إلى 2، من 2 إلى 4، من 3 إلى 6).
4. التمثيل البياني (Graphing): تُمكننا الرسوم البيانية من رؤية العلاقة بشكل مرئي. في النظام الإحداثي الديكارتي، يُنظر إلى كل زوج مرتب (x,y) كنقطة على المستوى.
   • (تصور نقاط (1,2), (2,4), (3,6) مرسومة على شبكة إحداثيات).
5. القاعدة أو المعادلة: عندما تكون العلاقة منتظمة وتتبع نمطًا معينًا، يمكن التعبير عنها بقاعدة أو معادلة رياضية. هذه هي الطريقة الأكثر شيوعًا وفعالية للتمثيل في الجبر. مثال: y=2x (للعلاقة R = {(1, 2), (2, 4), (3, 6)})

أنواع العلاقات (من منظور الدوال)

في سياق العلاقات بين مجموعتين، يمكن تصنيفها بناءً على كيفية ارتباط عناصر المجال بعناصر المدى. تُعد الدوال نوعًا خاصًا من العلاقات.

1. علاقة واحد إلى واحد (One-to-One Relation): كل عنصر في المجال يرتبط بعنصر واحد فقط في المدى، وكل عنصر في المدى يرتبط بعنصر واحد فقط في المجال. مثال: y=x+1 (كل x لها y فريدة، وكل y لها x فريدة).
2. علاقة واحد إلى كثير (One-to-Many Relation): كل عنصر في المجال يرتبط بعنصر واحد فقط في المدى. (هذه هي الدالة (Function)). مثال: y=x2 (كل x لها y واحدة، لكن y واحدة قد تكون ناتجة عن أكثر من x، مثل y=4 ناتجة عن x=2 و x=−2).
3. علاقة كثير إلى واحد (Many-to-One Relation): عنصر واحد في المجال يرتبط بأكثر من عنصر في المدى. (هذه ليست دالة). مثال: x=y2 (عندما x=4, y يمكن أن تكون 2 أو -2).
4. علاقة كثير إلى كثير (Many-to-Many Relation): عنصر واحد في المجال يرتبط بأكثر من عنصر في المدى، وعنصر واحد في المدى يرتبط بأكثر من عنصر في المجال. (هذه ليست دالة). مثال: العلاقة “صديق لـ” بين مجموعة من الأشخاص (شخص واحد قد يكون صديقًا لعدة أشخاص، وشخص ما قد يكون صديقًا لعدة أشخاص آخرين).

خصائص العلاقات (من منظور العلاقات الثنائية على مجموعة واحدة)

عندما تُعرف العلاقة على مجموعة واحدة (أي أن المجال والمدى هما نفس المجموعة)، فإن لها خصائص تُحدد طبيعتها:

لنفترض أن R هي علاقة معرفة على مجموعة A.

1. العلاقة الانعكاسية (Reflexive Relation): إذا كان كل عنصر في المجموعة A يرتبط بنفسه في العلاقة. أي، لكل a∈A، يكون (a,a)∈R. مثال: العلاقة “يساوي” (=) على مجموعة الأعداد الحقيقية. x=x دائمًا.
2. العلاقة التناظرية (Symmetric Relation): إذا كان (a,b)∈R، فإن (b,a)∈R دائمًا. مثال: العلاقة “صديق لـ” (إذا كان علي صديقًا لسارة، فإن سارة صديقة لعلي).
3. العلاقة المتعدية (Transitive Relation): إذا كان (a,b)∈R و (b,c)∈R، فإن (a,c)∈R دائمًا. مثال: العلاقة “أكبر من” (>) على مجموعة الأعداد الحقيقية. إذا كان x>y و y>z، فإن x>z.
4. العلاقة غير التناظرية (Antisymmetric Relation): إذا كان (a,b)∈R و (b,a)∈R، فإن a=b. مثال: العلاقة “أقل من أو يساوي” (≤) على مجموعة الأعداد الحقيقية. إذا كان x≤y و y≤x، فإن x=y.
5. العلاقة اللا انعكاسية (Irreflexive Relation): إذا لم يرتبط أي عنصر بنفسه في العلاقة. أي، لكل a∈A، يكون (a,a)∈/R. مثال: العلاقة “أكبر من” (>) على مجموعة الأعداد الحقيقية. x>x ليست صحيحة أبدًا.

أنواع خاصة من العلاقات

1. علاقة التكافؤ (Equivalence Relation): هي علاقة انعكاسية وتناظرية ومتعدية. تُقسم علاقة التكافؤ المجموعة إلى فئات من العناصر المتكافئة. مثال: العلاقة “يساوي” (=) على مجموعة الأعداد الحقيقية.
2. علاقة الترتيب الجزئي (Partial Order Relation): هي علاقة انعكاسية وغير تناظرية ومتعدية. تُستخدم لوصف ترتيب بين العناصر قد لا تكون جميعها قابلة للمقارنة. مثال: العلاقة “أقل من أو يساوي” (≤) على مجموعة الأعداد الحقيقية.
3. علاقة الترتيب الكلي (Total Order Relation): هي علاقة ترتيب جزئي، بالإضافة إلى أن كل عنصرين في المجموعة قابلين للمقارنة (أي a≤b أو b≤a). مثال: العلاقة “أقل من أو يساوي” (≤) على مجموعة الأعداد الحقيقية.

أهمية العلاقات في الرياضيات وتطبيقاتها

تُعد العلاقات مفهومًا محوريًا في الرياضيات ولها تطبيقات واسعة في مجالات متنوعة:

• أساس الدوال: الدوال هي نوع خاص ومهم من العلاقات، وفهم العلاقات يُعد تمهيدًا ضروريًا لدراسة الدوال.
• المنطق وعلوم الحاسوب: تُستخدم العلاقات في تصميم قواعد البيانات، وتطوير الخوارزميات، ونظرية الرسوم البيانية (Graph Theory)، التي تُطبق في الشبكات والتحسين.
• نظرية المجموعات: تُعرف العلاقات نفسها باستخدام مفاهيم المجموعات.
• الإحصاء وتحليل البيانات: تُستخدم العلاقات لوصف الارتباطات بين مجموعات البيانات والمتغيرات.
• الهندسة: تُستخدم العلاقات لوصف الخصائص الهندسية للأشكال والمواقع.
• الفيزياء والعلوم الطبيعية: تُستخدم المعادلات (وهي علاقات) لوصف القوانين الفيزيائية والعلاقات بين الكميات.
• الحياة اليومية: العلاقات موجودة في كل مكان حولنا، مثل علاقة “الأب والابن”، “المعلم والطالب”، “العمل والراتب”. الرياضيات تُوفر الأدوات لوصف وتحليل هذه العلاقات بشكل دقيق.

الخاتمة

تُشكل العلاقات حجر الزاوية في بناء الفهم الرياضي، فهي تُقدم إطارًا منظمًا لوصف الترابط بين العناصر والمجموعات. من خلال مفهوم الزوج المرتب والمجال والمدى، وبتنوع طرق التمثيل من القوائم والجداول إلى الرسوم البيانية والمعادلات، تُصبح العلاقات أدوات قوية لتحليل الأنماط وحل المشكلات. إن استيعاب الأنواع المختلفة للعلاقات وخصائصها، مثل الانعكاسية والتناظرية والتعدية، يُمكننا من تصنيفها وفهم سلوكها بشكل أعمق، ويُمهد الطريق لدراسة مفاهيم أكثر تعقيدًا مثل الدوال وأنواع الترتيب والتكافؤ. في نهاية المطاف، لا تُعد العلاقات مجرد مفاهيم نظرية بحتة، بل هي مفتاح لفهم العالم من حولنا وتطبيقاته العملية في شتى العلوم والمجالات، مما يُبرز دور الرياضيات كأداة أساسية في فك شفرة تعقيدات الكون.