المتتابعات
مقدمة
في عالم الرياضيات، غالبًا ما نصادف مجموعات من الأعداد أو القيم مرتبة وفقًا لقاعدة أو نمط محدد. تُعرف هذه المجموعات بالمتتابعات، وتمثل سلسلة من العناصر (عادةً أعداد) تتبع ترتيبًا معينًا. يمكن أن تكون هذه المتتابعات منتهية (لها عدد محدد من العناصر) أو غير منتهية (تمتد إلى ما لا نهاية). إن فهم مفهوم المتتابعة وأنواعها المختلفة، وطرق تمثيلها وصيغها الرياضية (مثل الصيغة الحدية والصيغة الاسترجاعية)، وإدراك أهميتها في التحليل الرياضي وحساب التفاضل والتكامل والعديد من فروع العلوم التطبيقية، يمثل أساسًا ضروريًا لاستكشاف الأنماط العددية وفهم سلوك الدوال والعمليات الرياضية على نطاق أوسع.
مفهوم المتتابعة وأنواعها المختلفة
مفهوم المتتابعة (Sequence): هي دالة مجالها مجموعة الأعداد الطبيعية N={1,2,3,…} (للمتتابعات غير المنتهية التي تبدأ بالحد الأول) أو مجموعة جزئية من الأعداد الطبيعية {1,2,…,n} (للمتتابعات المنتهية ذات n حدًا)، ومدى هذه الدالة هو مجموعة من الأعداد الحقيقية (أو أي مجموعة أخرى). غالبًا ما يُشار إلى عناصر المتتابعة بالرمز an حيث n هو رقم الحد في المتتابعة.
أنواع المتتابعات:
- المتتابعات المنتهية (Finite Sequences): هي المتتابعات التي لها عدد محدد من الحدود. مثال: (2, 4, 6, 8, 10) هي متتابعة منتهية لها 5 حدود.
- المتتابعات غير المنتهية (Infinite Sequences): هي المتتابعات التي تستمر إلى ما لا نهاية. مثال: (1, 2, 3, 4, …) هي متتابعة غير منتهية تمثل الأعداد الطبيعية.
- المتتابعات المتزايدة (Increasing Sequences): هي المتتابعات التي يكون فيها كل حد أكبر من الحد الذي يسبقه (an+1>an لجميع قيم n). مثال: (1, 3, 5, 7, …).
- المتتابعات المتناقصة (Decreasing Sequences): هي المتتابعات التي يكون فيها كل حد أصغر من الحد الذي يسبقه (an+1<an لجميع قيم n) مثال: (10, 8, 6, 4,…).
- المتتابعات الثابتة (Constant Sequences): هي المتتابعات التي تكون فيها جميع الحدود متساوية (an+1=an لجميع قيم n). مثال: (3, 3, 3, 3, …).
- المتتابعات المتقاربة (Convergent Sequences): هي المتتابعات غير المنتهية التي تقترب حدودها من قيمة حدية معينة كلما زاد رقم الحد (n→∞).
- المتتابعات المتباعدة (Divergent Sequences): هي المتتابعات غير المنتهية التي لا تقترب حدودها من قيمة حدية معينة. يمكن أن تتباعد بالزيادة أو النقصان بلا حدود أو تتذبذب بين قيمتين أو أكثر.
تمثيل المتتابعات وصيغها الرياضية
تمثيل المتتابعات:
- ذكر العناصر: يمكن تمثيل المتتابعة عن طريق سرد عدد قليل من حدودها الأولى مع الإشارة إلى استمرارها إذا كانت غير منتهية، مثل (2, 4, 6, …).
- التمثيل البياني: يمكن تمثيل حدود المتتابعة كنقاط على المستوى الإحداثي حيث يمثل رقم الحد (n) الإحداثي السيني وقيمة الحد (an) الإحداثي الصادي.
صيغ المتتابعات:
- الصيغة الحدية (Explicit Formula): هي صيغة رياضية تعبر عن قيمة الحد an بدلالة رقم الحد n. مثال: المتتابعة (2, 4, 6, …) يمكن التعبير عنها بالصيغة an=2n.
- الصيغة الاسترجاعية (Recursive Formula): هي صيغة رياضية تعبر عن قيمة الحد an بدلالة حد أو أكثر من الحدود التي تسبقه، بالإضافة إلى تحديد قيمة الحد أو الحدود الأولى. مثال: متتابعة فيبوناتشي (1, 1, 2, 3, 5, …) يمكن التعبير عنها بالصيغة الاسترجاعية a1=1,a2=1,an=an−1+an−2 لـ n>2.
أمثلة على متتابعات مشهورة:
- المتتابعة الحسابية (Arithmetic Sequence): هي متتابعة يكون فيها الفرق بين أي حد والحد الذي يسبقه ثابتًا، ويُعرف هذا الفرق بالأساس (d). صيغتها الحدية هي an=a1+(n−1)d. مثال: (2, 5, 8, 11, …).
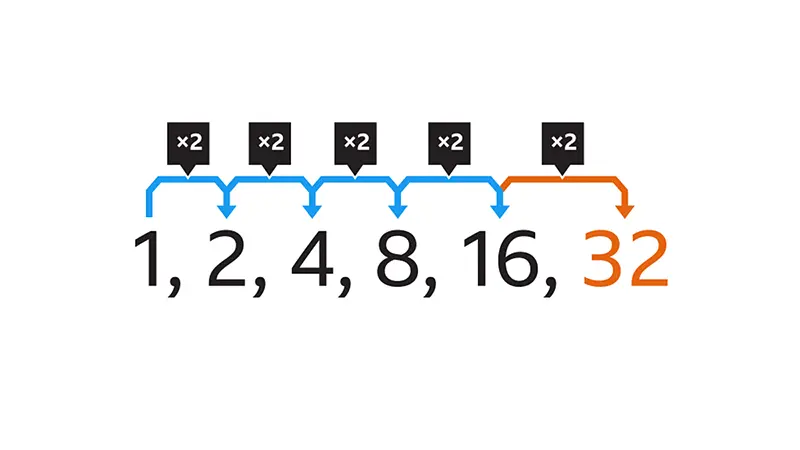
- المتتابعة الهندسية (Geometric Sequence): هي متتابعة يكون فيها حاصل قسمة أي حد على الحد الذي يسبقه ثابتًا، ويُعرف هذا الحاصل بالنسب (r). صيغتها الحدية هي an=a1⋅rn−1. مثال: (3, 6, 12, 24, …).
- متتابعة فيبوناتشي (Fibonacci Sequence): تم تعريفها بالصيغة الاسترجاعية a1=1,a2=1,an=an−1+an−2. تظهر في العديد من الظواهر الطبيعية.
أهمية المتتابعات وتطبيقاتها المتنوعة
تعتبر المتتابعات مفهومًا أساسيًا في العديد من فروع الرياضيات والعلوم التطبيقية:
- التحليل الرياضي: تعتبر دراسة تقارب وتباعد المتتابعات نقطة انطلاق لفهم النهايات والاستمرار والتفاضل والتكامل. مفهوم نهاية الدالة يُعرّف باستخدام نهايات المتتابعات.
- حساب التفاضل والتكامل: تلعب المتتابعات دورًا هامًا في تعريف التكامل (كتكامل ريمان الذي يعتمد على مجاميع ريمان التي هي متتابعات) وفي دراسة سلاسل القوى ومتسلسلات تايلور وماكلورين.
- البرمجة وعلوم الحاسوب: تُستخدم المتتابعات لتمثيل هياكل البيانات مثل القوائم والمصفوفات. كما تظهر في تحليل الخوارزميات (مثل عدد العمليات في خطوات متتابعة) وفي توليد الأرقام العشوائية.
- الاحتمالات والإحصاء: تُستخدم المتتابعات في دراسة العمليات العشوائية وسلاسل ماركوف.
- الفيزياء: تظهر المتتابعات في وصف حركة الجسيمات في أبعاد منفصلة، وفي تحليل الاهتزازات والموجات، وفي دراسة النظم الديناميكية.
- الهندسة: تُستخدم المتتابعات في تعريف بعض المنحنيات والأشكال الهندسية (مثل حدود كسور معينة).
- الاقتصاد والمالية: تُستخدم المتتابعات في نمذجة النمو الاقتصادي، وحساب الفوائد المركبة، وتحليل سلاسل البيانات الزمنية.
- علم الأحياء: تظهر متتابعات في تحليل تسلسل الحمض النووي (DNA) والبروتينات.
الخاتمة
تُعد المتتابعات لبنة أساسية في بناء الفهم الرياضي للأنماط والتغيرات. من خلال تحديد أنواعها وتمثيلها باستخدام الصيغ المختلفة، نكتسب القدرة على وصف وتحليل السلوك المنتظم وغير المنتظم للقيم. إن تطبيقات المتتابعات الواسعة في فروع الرياضيات المختلفة والعلوم التطبيقية تؤكد على أهميتها كأداة قوية لاستكشاف الأنماط، ونمذجة العمليات، وفهم العالم من حولنا. مع استمرار تطور العلوم والتكنولوجيا، ستظل دراسة المتتابعات والتعمق في خصائصها ذات أهمية بالغة في فتح آفاق جديدة للمعرفة والتطبيق.


