مقدمة

في عالم الهندسة التحليلية والجبر، يُعد مفهوم ميل المستقيم (Slope) من المفاهيم الأساسية التي تصف خاصية هامة للخطوط المستقيمة وهي انحدارها واتجاهها. يمثل الميل مقياسًا كميًا لمقدار التغير الرأسي (الصادي) للخط لكل وحدة تغير أفقي (سيني). إن فهم مفهوم ميل المستقيم وأهميته، واستيعاب طريقة حسابه باستخدام إحداثيات نقطتين صحيحتين تقعان على الخط، وإدراك تفسيره الفيزيائي والهندسي، يمثل أساسًا ضروريًا لتحليل العلاقات الخطية ووصف التغير المنتظم في العديد من الظواهر الرياضية والعلمية. فالميل لا يقتصر على كونه قيمة عددية تصف انحدار الخط، بل يحمل في طياته معلومات قيمة عن معدل التغير واتجاه العلاقة بين المتغيرات التي يمثلها الخط.

مفهوم ميل المستقيم وأهميته

مفهوم ميل المستقيم (Slope of a Line): هو عدد يصف انحدار الخط المستقيم واتجاهه على المستوى الإحداثي. يمثل الميل مقدار التغير الرأسي (التغير في الإحداثي الصادي، Δy) لكل وحدة تغير أفقي (التغير في الإحداثي السيني، Δx) بين أي نقطتين مختلفتين تقعان على الخط.

أهمية ميل المستقيم:

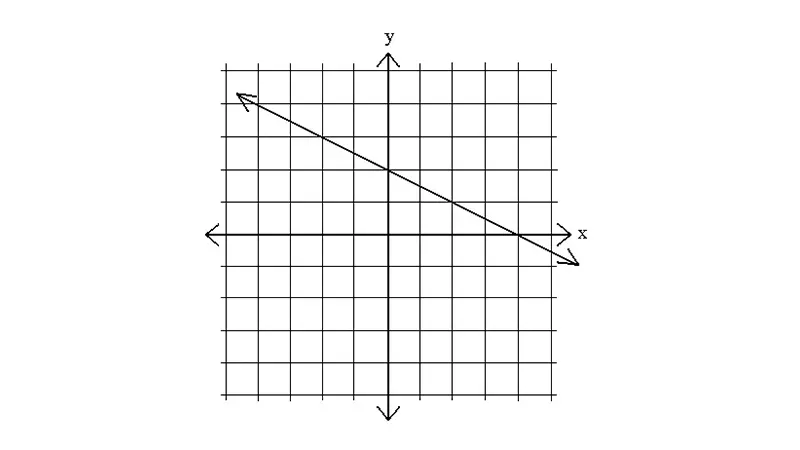
• وصف انحدار الخط: يحدد الميل ما إذا كان الخط صاعدًا (ميل موجب)، أو هابطًا (ميل سالب)، أو أفقيًا (ميل صفر).
• قياس معدل التغير: في سياق الدوال الخطية التي تمثل علاقات بين متغيرين، يمثل الميل معدل التغير الثابت للمتغير التابع بالنسبة للمتغير المستقل.
• تحديد توازي وتعامد الخطوط: خطان مستقيمان غير رأسيين متوازيان إذا كان لهما نفس الميل. خطان مستقيمان غير رأسيين ومتعامدان إذا كان حاصل ضرب ميلهما يساوي سالب واحد (في هذا البحث، سنركز على حالات الميل الصحيح).
• تحليل العلاقات الخطية: يساعد الميل في فهم قوة واتجاه العلاقة الخطية بين المتغيرات في النماذج الرياضية والإحصائية.
• التطبيقات الفيزيائية والهندسية: يستخدم الميل في وصف السرعة، والتسارع (في سياقات مبسطة)، وانحدار الأسطح، وزوايا الميل.

تفسير ميل المستقيم وتطبيقاته

التفسير الهندسي للميل: يمثل الميل مقدار “ارتفاع” الخط أو “انخفاضه” لكل وحدة “امتداد” أفقي. الميل الموجب يعني أن الخط يرتفع عند التحرك من اليسار إلى اليمين، والميل السالب يعني أن الخط ينخفض، والميل الصفر يعني أن الخط أفقي، والميل غير المعرف يعني أن الخط رأسي.

التفسير الفيزيائي للميل: في العديد من التطبيقات الفيزيائية، يمثل ميل الخط معدل تغير كمية فيزيائية بالنسبة لكمية أخرى. على سبيل المثال:

• في الرسم البياني للمسافة مقابل الزمن لحركة منتظمة، يمثل الميل السرعة الثابتة (إذا كانت السرعة عددًا صحيحًا).
• في الرسم البياني للجهد مقابل التيار في مقاومة ثابتة (قانون أوم)، يمثل الميل قيمة المقاومة (إذا كانت المقاومة عددًا صحيحًا).

تطبيقات ميل المستقيم في الرياضيات والعلوم:

• تحديد معادلة الخط المستقيم: إذا علمنا ميل الخط ونقطة يمر بها (أو المقطع الصادي)، يمكننا تحديد معادلة الخط المستقيم.
• التحقق من استقامة النقاط: إذا كانت مجموعة من النقاط تقع على نفس الخط المستقيم، فإن ميل الخط بين أي زوج من هذه النقاط يجب أن يكون هو نفسه.
• تحليل النمو الخطي: في النماذج التي تصف النمو الخطي (مثل نمو نبات بمعدل ثابت)، يمثل الميل معدل النمو.
• حساب الانحدار في التضاريس: يستخدم مفهوم الميل (أو الانحدار المئوي) في الجغرافيا والهندسة المدنية لوصف انحدار الأراضي والطرق.

أمثلة على تطبيقات ميل المستقيم بقيم صحيحة:

• سيارة تتحرك بسرعة ثابتة: إذا كانت سيارة تتحرك بسرعة ثابتة 20 مترًا في الثانية، فإن الرسم البياني للمسافة مقابل الزمن سيكون خطًا مستقيمًا يمر بنقطة الأصل وميله يساوي 20.
• زيادة طول شمعة تحترق بمعدل ثابت: إذا كانت شمعة طولها 30 سم وتحترق بمعدل 2 سم في الساعة، فإن العلاقة بين طول الشمعة والزمن يمكن تمثيلها بخط مستقيم ميله -2 (لأن الطول يتناقص).
• تكلفة إنتاج عدد من المنتجات بتكلفة متغيرة ثابتة: إذا كانت تكلفة إنتاج الوحدة الواحدة 5 دولارات، فإن العلاقة بين التكلفة الكلية وعدد الوحدات المنتجة هي خط مستقيم يمر بنقطة الأصل وميله يساوي 5.

الخاتمة

يُعد ميل المستقيم مفهومًا أساسيًا وقويًا في الرياضيات والعلوم، حيث يوفر وسيلة كمية لوصف انحدار الخطوط المستقيمة ومعدل التغير المنتظم بين المتغيرات. من خلال حسابه باستخدام إحداثيات نقطتين صحيحتين وتفسيره الهندسي والفيزيائي، نكتسب رؤى قيمة حول طبيعة العلاقات الخطية وتطبيقاتها المتنوعة في وصف وتحليل الظواهر المختلفة. إن فهم ميل المستقيم يمثل لبنة أساسية في بناء فهم أعمق للجبر التحليلي والدوال الخطية وتطبيقاتها العملية.