مقدمة

في سياق الجبر، لا تقتصر العلاقات بين الكميات دائمًا على شرط واحد؛ ففي كثير من الأحيان، يجب أن يُلبي المتغير شروطًا متعددة في آن واحد ليُعد حلًا صحيحًا. هنا يبرز مفهوم المتباينات المركبة (Compound Inequalities)، وهي عبارات رياضية تتكون من متباينتين بسيطتين أو أكثر متصلتين بكلمة “و” (AND) أو “أو” (OR). تُعد هذه المتباينات أداة قوية لوصف القيود الأكثر تعقيدًا في الواقع، حيث تُمكننا من تحديد مجموعات الحلول التي تقع ضمن نطاقات محددة أو تُمثل اتحادات لمجموعات حلول متعددة. إن فهم كيفية تحليل هذه المتباينات وخطوات حلها، مع التمييز الواضح بين روابط “و” و “أو”، يُعد مهارة أساسية تُمكننا من تفسير الظواهر التي تتضمن شروطًا متداخلة أو بديلة، مثل نطاقات درجات الحرارة الآمنة، أو المتطلبات المالية المشروطة، أو مواصفات جودة المنتجات. يهدف هذا البحث إلى استكشاف بنية المتباينات المركبة، وتوضيح طرق حلها وتمثيل مجموعات الحلول بيانيًا، مما يُسهم في تعميق فهمنا لكيفية التعامل مع القيود المتعددة في التحليل الجبري والتطبيقات العملية.

مفهوم المتباينة المركبة وأنواعها

المتباينة المركبة (Compound Inequality): هي متباينة تتكون من متباينتين بسيطتين أو أكثر يتم ربطهما باستخدام الروابط المنطقية “و” (AND) أو “أو” (OR). الهدف من حلها هو إيجاد مجموعة القيم التي تحقق كل الشروط في حالة “و”، أو تحقق أحد الشروط على الأقل في حالة “أو”.

أنواع المتباينات المركبة:

1. المتباينات المركبة بـ “و” (AND Compound Inequalities):
   • تُشير هذه المتباينات إلى أن المتغير يجب أن يُلبي جميع الشروط المحددة في المتباينات الفردية في نفس الوقت.
   • تُمثل مجموعة حل هذه المتباينات تقاطع مجموعتي الحل للمتباينتين الفرديتين.
   • غالبًا ما تُكتب هذه المتباينات في شكل مُكثف، حيث يكون المتغير محصورًا بين قيمتين.
     • مثال: س أكبر من 2 و س أصغر من 7. (يمكن كتابتها 2 أصغر من س أصغر من 7).
     • معناها أن س يجب أن تكون أكبر من 2 وفي نفس الوقت أصغر من 7.

2. المتباينات المركبة بـ “أو” (OR Compound Inequalities):
   • تُشير هذه المتباينات إلى أن المتغير يجب أن يُلبي أحد الشرطين على الأقل (أو كلاهما).
   • تُمثل مجموعة حل هذه المتباينات اتحاد مجموعتي الحل للمتباينتين الفرديتين.
   • تُكتب دائمًا كعبارتين منفصلتين متصلتين بالكلمة “أو”.
     • مثال: س أصغر من 1 أو س أكبر من 5.
     • معناها أن س يمكن أن تكون أي عدد أصغر من 1، أو أي عدد أكبر من 5. لا يشترط أن تكون س ضمن نطاق واحد.

خصائص المتباينات الأساسية (مراجعة مختصرة)

قبل البدء في حل المتباينات المركبة، نُذكر بالخصائص الأساسية لعمليات الجمع والطرح والضرب والقسمة على المتباينات، والتي تُطبق على كل جزء من المتباينة المركبة على حدة:

1. خاصية الإضافة والطرح: عند إضافة أو طرح نفس الكمية من كلا طرفي المتباينة، لا يتغير اتجاه علامة المتباينة.
   • إذا كان أ < ب، فإن أ + ج < ب + ج.
   • إذا كان أ > ب، فإن أ – ج > ب – ج.
2. خاصية الضرب والقسمة على عدد موجب: عند ضرب أو قسمة كلا طرفي المتباينة على نفس الكمية الموجبة، لا يتغير اتجاه علامة المتباينة.
   • إذا كان أ < ب و ج > 0، فإن أ مضروبًا في جـ < ب مضروبًا في جـ.
   • إذا كان أ > ب و ج > 0، فإن أ مقسومًا على جـ > ب مقسومًا على جـ.
3. خاصية الضرب والقسمة على عدد سالب: عند ضرب أو قسمة كلا طرفي المتباينة على نفس الكمية السالبة، ينعكس اتجاه علامة المتباينة.
   • إذا كان أ < ب و ج < 0، فإن أ مضروبًا في جـ > ب مضروبًا في جـ.
   • إذا كان أ > ب و ج < 0، فإن أ مقسومًا على جـ < ب مقسومًا على جـ.
   • هذه القاعدة حاسمة ويجب الانتباه إليها جيدًا عند حل المتباينات.

خطوات حل المتباينات المركبة بـ “و”

تُحل المتباينات المركبة بـ “و” بطريقتين رئيسيتين:

الطريقة الأولى: الحل في صورة متباينة ثلاثية الأجزاء (إذا كانت ممكنة)

هذه الطريقة فعالة عندما يكون المتغير في الجزء الأوسط من المتباينة ويتم تطبيق نفس العمليات على جميع الأجزاء.

1. عزل المتغير في الجزء الأوسط: قم بتطبيق العمليات العكسية (جمع، طرح، ضرب، قسمة) على جميع أجزاء المتباينة (الطرف الأيسر، الطرف الأوسط، الطرف الأيمن) لعزل المتغير في المنتصف.
2. تذكر قاعدة الضرب والقسمة على عدد سالب: إذا ضربت أو قسمت جميع الأجزاء على عدد سالب، يجب أن تعكس اتجاه علامتي المتباينة.
3. كتابة مجموعة الحل: غالبًا ما تكون مجموعة الحل في شكل نطاق (فترة).

مثال 1: حل المتباينة: 2 أصغر من س زائد 3 أصغر من أو تساوي 8

1. عزل س: نطرح 3 من جميع الأجزاء: 2 ناقص 3 أصغر من س زائد 3 ناقص 3 أصغر من أو تساوي 8 ناقص 3 سالب 1 أصغر من س أصغر من أو تساوي 5
2. مجموعة الحل: الأعداد بين سالب 1 و 5، شاملة 5 وغير شاملة سالب 1.
   • التمثيل البياني على خط الأعداد: دائرة مفتوحة عند سالب 1، دائرة مغلقة عند 5، وخط يربط بينهما.
   • الترميز الفتري: (سالب 1، 5].

مثال 2: حل المتباينة: سالب 10 أصغر من أو تساوي سالب 2س أصغر من 6

1. عزل س: نقسم جميع الأجزاء على سالب 2. يجب عكس اتجاه علامتي المتباينة. سالب 10 مقسومًا على سالب 2 أكبر من أو تساوي سالب 2س مقسومًا على سالب 2 أكبر من 6 مقسومًا على سالب 2 5 أكبر من أو تساوي س أكبر من سالب 3
2. إعادة ترتيب للوضوح: من الأفضل دائمًا كتابة المتباينة بحيث يكون العدد الأصغر على اليسار والعدد الأكبر على اليمين. سالب 3 أصغر من س أصغر من أو تساوي5
3. مجموعة الحل: الأعداد بين سالب 3 و 5، شاملة 5 وغير شاملة سالب 3.
   • التمثيل البياني: دائرة مفتوحة عند سالب 3، دائرة مغلقة عند 5، وخط يربط بينهما.
   • الترميز الفتري: (سالب 3، 5].

الطريقة الثانية: الحل كعبارتين منفصلتين (دائمًا ممكنة)

يمكن دائمًا تفكيك المتباينة المركبة بـ “و” إلى متباينتين بسيطتين وحل كل منهما على حدة، ثم إيجاد التقاطع.

1. فصل المتباينة المركبة: إلى متباينتين بسيطتين منفصلتين.
2. حل كل متباينة: باستخدام الخطوات العادية لحل المتباينات.
3. إيجاد تقاطع الحلول: قم بتمثيل كل مجموعة حل على خط أعداد منفصل، ثم ابحث عن الجزء الذي تتداخل فيه مجموعتا الحل. هذا الجزء المشترك هو مجموعة الحل للمتباينة المركبة الأصلية.

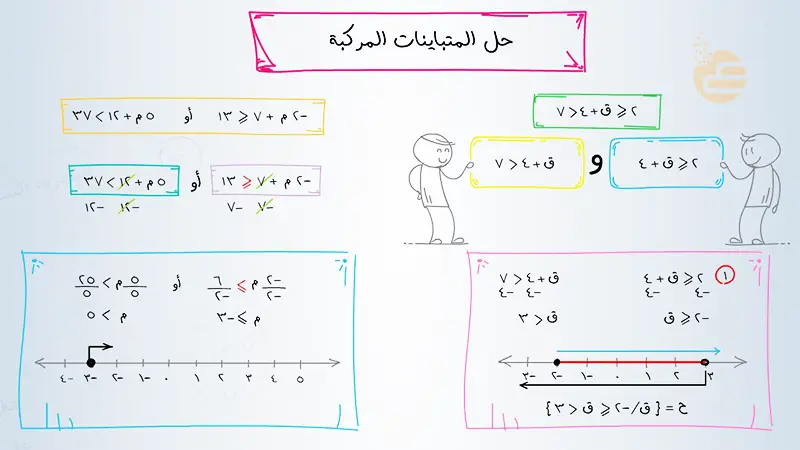
مثال 3: حل المتباينة: 4س زائد 1 أكبر من 9 و 3س ناقص 5 أصغر من أو تساوي 10

1. حل المتباينة الأولى: 4س زائد 1 أكبر من 9 4س أكبر من 9 ناقص 1 4س أكبر من 8 س أكبر من 2
2. حل المتباينة الثانية: 3س ناقص 5 أصغر من أو تساوي 10 3س أصغر من أو تساوي 10 زائد 5 3س أصغر من أو تساوي 15 س أصغر من أو تساوي 5
3. إيجاد التقاطع (و): التقاطع هو الأعداد التي هي أكبر من 2 و أصغر من أو تساوي5.
   • مجموعة الحل: 2 أصغر من س أصغر من أو تساوي 5.
   • التمثيل البياني: دائرة مفتوحة عند 2، دائرة مغلقة عند 5، وخط يربط بينهما.
   • الترميز الفتري: (2، 5].

خطوات حل المتباينات المركبة بـ “أو”

تُحل المتباينات المركبة بـ “أو” دائمًا عن طريق حل المتباينتين البسيطتين بشكل منفصل ثم إيجاد الاتحاد.

1. حل كل متباينة: باستخدام الخطوات العادية لحل المتباينات.
2. إيجاد اتحاد الحلول: قم بتمثيل كل مجموعة حل على خط أعداد منفصل، ثم اجمع جميع الأجزاء التي يُغطيها أي من الخطين (تداخل أو عدم تداخل).

مثال 4: حل المتباينة: س ناقص 3 أصغر من 2 أو س زائد 5 أكبر من أو تساوي 9

1. حل المتباينة الأولى: س ناقص 3 أصغر من 2 س أصغر من 2 زائد 3 س أصغر من 5
2. حل المتباينة الثانية: س زائد 5 أكبر من أو تساوي 9 س أكبر من أو تساوي 9 ناقص 5 س أكبر من أو تساوي 4
3. إيجاد الاتحاد (أو): مجموعة الحل هي الأعداد التي هي أصغر من 5 أو أكبر من أو تساوي 4. عند النظر إلى خط الأعداد، نلاحظ أن الأعداد الأصغر من 5 تشمل كل الأعداد وصولًا إلى ما لا نهاية سالبًا، والأعداد الأكبر من أو تساوي 4 تشمل كل الأعداد وصولًا إلى ما لا نهاية موجبًا. هاتان المجموعتان تتداخلان وتُغطيان كل خط الأعداد.
   • مجموعة الحل: جميع الأعداد الحقيقية.
   • التمثيل البياني: خط أعداد مظلل بالكامل (من سالب ما لا نهاية إلى موجب ما لا نهاية).
   • الترميز الفتري: (سالب ما لا نهاية، موجب ما لا نهاية).

مثال 5: حل المتباينة: 2س زائد 1 أصغر من سالب 5 أو 3س ناقص 4 أكبر من 8

1. حل المتباينة الأولى: 2س زائد 1 أصغر من سالب 5 2س أصغر من سالب 5 ناقص 1 2س أصغر من سالب 6 س أصغر من سالب 3
2. حل المتباينة الثانية: 3س ناقص 4 أكبر من 8 3س أكبر من 8 زائد 4 3س أكبر من 12 س أكبر من 4
3. إيجاد الاتحاد (أو): مجموعة الحل هي الأعداد التي هي أصغر من سالب 3 أو أكبر من 4.
   • مجموعة الحل: لا يوجد تداخل بين المجموعتين.
   • التمثيل البياني: دائرة مفتوحة عند سالب 3 وسهم لليسار. دائرة مفتوحة عند 4 وسهم لليمين. (فجوة بين المجموعتين).
   • الترميز الفتري: (سالب ما لا نهاية، سالب 3) اتحاد (4، موجب ما لا نهاية).

تطبيقات المتباينات المركبة في الحياة الواقعية

تُعد المتباينات المركبة أدوات قوية لوصف و حل المشكلات التي تتضمن شروطًا معقدة أو بدائل:

1. الصحة والسلامة: تحديد نطاقات درجات الحرارة أو الرطوبة الآمنة.
   • مثال: للحفاظ على سلامة الغذاء، يجب أن تكون درجة الحرارة (د) أكبر من أو تساوي 0 درجة مئوية و أصغر من أو تساوي 5 درجات مئوية. تُكتب 0 أصغر من أو تساوي د أصغر من أو تساوي 5.
2. المالية والاقتصاد: تحديد نطاقات الدخل المؤهل للحصول على مزايا معينة، أو الشروط لتقديم العروض.
   • مثال: لتكون مؤهلاً للحصول على قرض، يجب أن يكون دخلك الشهري (د) أكبر من 3000 دولار أو أن يكون لديك رصيد بنكي (ر) أكبر من 20000 دولار.
3. العلوم والهندسة: تحديد نطاقات القياسات المسموح بها أو الظروف التجريبية.
   • مثال: يجب أن يكون ضغط المحرك (ض) أكبر من 100 كيلو باسكال و أصغر من 200 كيلو باسكال ليعمل بكفاءة. تُكتب 100 أصغر من ض أصغر من 200.
4. نظم التحكم والأتمتة: تحديد الشروط التي يجب أن تتحقق لتفعيل نظام معين.
   • مثال: سيعمل نظام التبريد إذا كانت درجة الحرارة (د) أكبر من 25 درجة مئوية أو إذا كانت الرطوبة (ر) أكبر من 80 بالمائة.
5. المسافات والسرعات: تحديد الفترات الزمنية أو المسافات التي تُلبي عدة شروط.
   • مثال: قد تكون على الطريق لمدة تتراوح بين ساعتين (2) وخمس ساعات (5) (2 أصغر من أو تساوي س أصغر من أو تساوي 5)، أو إذا كنت تسير بسرعة لا تقل عن 80 كيلومترًا في الساعة (ع أكبر من أو تساوي 80).

الخاتمة

تُمثل المتباينات المركبة خطوة متقدمة ومهمة في رحلة تعلم الجبر، حيث تُمكننا من التعبير عن شروط متعددة ومتداخلة بشكل دقيق. إن التمييز الواضح بين روابط “و” و “أو” هو مفتاح فهم طبيعة مجموعة الحل: فالأولى تُشير إلى التقاطع وتتطلب تحقيق جميع الشروط، بينما الثانية تُشير إلى الاتحاد وتتطلب تحقيق شرط واحد على الأقل. من خلال إتقان خطوات حل المتباينات البسيطة ثم تطبيقها بشكل منهجي على كل جزء من المتباينة المركبة، مع الانتباه الحاسم لقاعدة عكس علامة المتباينة عند الضرب أو القسمة على الأعداد السالبة، يُصبح بإمكاننا فك شفرة القيود المعقدة. لا تقتصر أهمية هذه المتباينات على التمارين الأكاديمية فحسب؛ بل تُعد أداة تحليلية قوية في مجالات لا حصر لها، مما يُعزز التفكير النقدي، ويُمكننا من اتخاذ قرارات مستنيرة في مواقف تتطلب فهمًا عميقًا للعلاقات اللامتساوية ومتغيراتها المتعددة.