مقدمة

في سياق الجبر، لا تُستخدم القيمة المطلقة فقط لتمثيل المسافة عن الصفر في المعادلات، بل تُصبح أداة قوية لوصف نطاقات قيم تقع ضمن مسافة معينة من نقطة مرجعية أو تتجاوزها عند استخدامها في المتباينات (Inequalities). تُقدم المتباينات التي تتضمن القيمة المطلقة تحديًا فريدًا وتتطلب فهمًا عميقًا لمفهوم المسافة الرياضية. فهي لا تُشير إلى نقطة واحدة أو نطاق مستمر بسيط، بل إلى مجموعة من النقاط التي تُلبي شروط المسافة المحددة. يُعد إتقان هذه المتباينات ضروريًا ليس فقط في الجبر المتقدم، بل في تطبيقات متنوعة تتطلب تحديد نطاقات التفاوت أو الحدود المقبولة، مثل التحكم في الجودة، أو تحليل الأخطاء في القياسات، أو حتى في فهم الفروقات في الظواهر الطبيعية. يهدف هذا البحث إلى تفكيك بنية المتباينات التي تتضمن القيمة المطلقة، وتوضيح كيفية تحويلها إلى متباينات مركبة بسيطة باستخدام قواعد محددة، ثم حلها وتمثيل مجموعات الحلول بيانيًا، مما يُسهم في تعزيز فهمنا لكيفية التعامل مع القيود المستندة إلى المسافة في التحليل الرياضي والتطبيقات العملية.

مفهوم القيمة المطلقة ومراجعة المتباينات الأساسية

قبل الغوص في المتباينات التي تتضمن القيمة المطلقة، دعنا نُراجع المفاهيم الأساسية:

• القيمة المطلقة: تُمثل المسافة بين العدد والصفر على خط الأعداد. تُرمز القيمة المطلقة للعدد x بالرمز ∣x∣.
  • رياضيًا:
    • ∣x∣=x إذا كان x أكبر من أو يساوي 0.
    • ∣x∣=سالب x إذا كان x أصغر من 0.
  • الخاصية الجوهرية: ناتج القيمة المطلقة دائمًا غير سالب (أكبر من أو يساوي صفرًا).
• مراجعة سريعة لخصائص المتباينات:
  • عند الجمع أو الطرح لنفس العدد من طرفي المتباينة، لا يتغير اتجاه العلامة.
  • عند الضرب أو القسمة على عدد موجب في طرفي المتباينة، لا يتغير اتجاه العلامة.
  • عند الضرب أو القسمة على عدد سالب في طرفي المتباينة، يجب عكس اتجاه العلامة.

المبادئ الأساسية لحل المتباينات التي تتضمن القيمة المطلقة

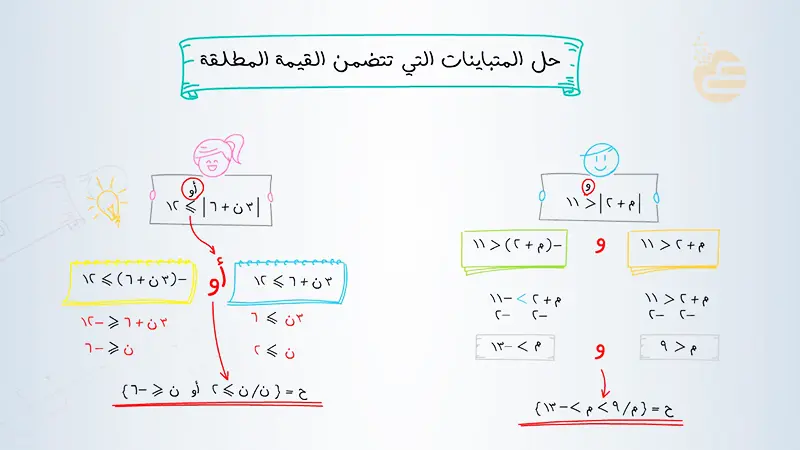
النهج الأساسي لحل المتباينات التي تتضمن القيمة المطلقة هو تحويلها إلى متباينة مركبة (تتضمن “و” أو “أو”)، ثم حل المتباينة المركبة الناتجة. يعتمد نوع المتباينة المركبة على اتجاه علامة المتباينة الأصلية.

هناك نوعان رئيسيان من المتباينات التي تتضمن القيمة المطلقة:

1. القيمة المطلقة أصغر من (أو أصغر من أو تساوي) عدد موجب:
   • الشكل العام: ∣ax+b∣<c أو ∣ax+b∣≤c (حيث c عدد موجب).
   • المبدأ: إذا كانت المسافة من الصفر أقل من c، فهذا يعني أن التعبير داخل القيمة المطلقة يقع بين −c و c.
   • التحويل: تُحول إلى متباينة مركبة بـ “و”:
     • −c<ax+b<c
     • أو −c≤ax+b≤c (إذا كانت العلامة الأصلية ≤)
   • سبب هذا التحويل: تخيل خط الأعداد. إذا كانت المسافة من الصفر أقل من 5 (مثلاً)، فإن الأعداد المحققة هي الأعداد بين -5 و 5 (أي س > -5 و س < 5).

2. القيمة المطلقة أكبر من (أو أكبر من أو تساوي) عدد موجب:
   • الشكل العام: ∣ax+b∣>c أو ∣ax+b∣≥c (حيث c عدد موجب).
   • المبدأ: إذا كانت المسافة من الصفر أكبر من c، فهذا يعني أن التعبير داخل القيمة المطلقة أكبر من c أو أصغر من −c.
   • التحويل: تُحول إلى متباينة مركبة بـ “أو”:
     • ax+b>c أو ax+b<−c
     • أو ax+b≥c أو ax+b≤−c (إذا كانت العلامة الأصلية ≥)
   • سبب هذا التحويل: تخيل خط الأعداد. إذا كانت المسافة من الصفر أكبر من 5 (مثلاً)، فإن الأعداد المحققة هي الأعداد الأكبر من 5، أو الأعداد الأصغر من -5.

الحالات الخاصة (معامل c):

• إذا كان c يساوي صفرًا:
  • ∣ax+b∣<0: لا يوجد حل (لأن القيمة المطلقة لا يمكن أن تكون سالبة).
  • ∣ax+b∣≤0: الحل الوحيد هو ax+b=0 (لأن القيمة المطلقة لا تكون سالبة أبدًا، والحل الوحيد هو أن تكون صفرًا).
  • ∣ax+b∣>0: الحل هو كل الأعداد الحقيقية باستثناء القيم التي تجعل ax+b=0.
  • ∣ax+b∣≥0: الحل هو جميع الأعداد الحقيقية (لأن القيمة المطلقة دائمًا أكبر من أو تساوي صفرًا).
• إذا كان c عددًا سالبًا:
  • ∣ax+b∣<عدد سالب: لا يوجد حل (القيمة المطلقة لا يمكن أن تكون أقل من عدد سالب).
  • ∣ax+b∣≤عدد سالب: لا يوجد حل.
  • ∣ax+b∣>عدد سالب: الحل هو جميع الأعداد الحقيقية (لأن القيمة المطلقة دائمًا موجبة، وهي دائمًا أكبر من أي عدد سالب).
  • ∣ax+b∣≥عدد سالب: الحل هو جميع الأعداد الحقيقية.

خطوات حل المتباينات التي تتضمن القيمة المطلقة (النهج المنهجي)

1. عزل تعبير القيمة المطلقة: يجب أن يكون تعبير القيمة المطلقة (الحد الذي يحتوي على علامة القيمة المطلقة) وحده في أحد طرفي المتباينة. تخلص من أي أعداد ثابتة مضافة أو مطروحة أو مضروبة أو مقسومة على تعبير القيمة المطلقة أولًا باستخدام العمليات العكسية.
   • تذكر: إذا قمت بالضرب أو القسمة على عدد سالب أثناء هذه الخطوة، اعكس علامة المتباينة حتى لو كانت القيمة المطلقة لا تزال موجودة.
2. تحديد نوع المتباينة المركبة:
   • إذا كان لديك ∣ax+b∣<c أو ∣ax+b∣≤c (أي “القيمة المطلقة أصغر من”): حولها إلى متباينة مركبة بـ “و”: −c<ax+b<c.
   • إذا كان لديك ∣ax+b∣>c أو ∣ax+b∣≥c (أي “القيمة المطلقة أكبر من”): حولها إلى متباينة مركبة بـ “أو”: ax+b>c أو ax+b<−c.
   • انتبه جيدًا لحالات c التي تساوي صفرًا أو تكون سالبة كما ذكرنا في القسم الثاني.
3. حل المتباينة المركبة الناتجة:
   • لمتباينات “و”: قم بحل المتباينة ثلاثية الأجزاء عن طريق تطبيق نفس العمليات على جميع الأجزاء (الطرف الأيسر، الطرف الأوسط، الطرف الأيمن) لعزل المتغير. تذكر عكس العلامات إذا قسمت أو ضربت في عدد سالب.
   • لمتباينات “أو”: قم بحل كل متباينة بسيطة على حدة.
4. تمثيل مجموعة الحل بيانيًا وكتابتها بالترميز الفتري:
   • لمتباينات “و”: تكون مجموعة الحل فترة واحدة على خط الأعداد (تقاطع).
     • دائرتان مفتوحتان أو مغلقان عند طرفي الفترة، وخط يربط بينهما.
   • لمتباينات “أو”: تكون مجموعة الحل فترتين منفصلتين غالبًا (اتحاد)، أو كل الأعداد الحقيقية إذا كان هناك تداخل كامل.
     • دائرتان مفتوحتان أو مغلقان عند طرفي الفترتين، وأسهم تتجه خارجًا من الدائرتين.

أمثلة تطبيقية متنوعة

مثال 1: القيمة المطلقة أصغر من عدد موجب

حل المتباينة: ∣x−4∣<3

1. عزل تعبير القيمة المطلقة: معزول بالفعل.
2. تحديد النوع والتحويل: “أصغر من” عدد موجب (3)، لذا نحولها إلى متباينة مركبة بـ “و”: −3<x−4<3
3. حل المتباينة المركبة: نضيف 4 إلى جميع الأجزاء: −3+4<x−4+4<3+4 1<x<7
4. مجموعة الحل: الأعداد بين 1 و 7، غير شاملة الطرفين.
   • التمثيل البياني: دائرة مفتوحة عند 1، دائرة مفتوحة عند 7، وخط يربط بينهما.
   • الترميز الفتري: (1، 7).

مثال 2: القيمة المطلقة أكبر من عدد موجب

حل المتباينة: ∣2x+1∣≥9

1. عزل تعبير القيمة المطلقة: معزول بالفعل.
2. تحديد النوع والتحويل: “أكبر من أو تساوي” عدد موجب (9)، لذا نحولها إلى متباينة مركبة بـ “أو”: 2x+1≥9 أو 2x+1≤−9
3. حل كل متباينة بسيطة:
   • الأولى: 2x+1≥9 2x≥9−1 2x≥8 x≥4 (قسمنا على 2 موجب، لم نعكس العلامة)
   • الثانية: 2x+1≤−9 2x≤−9−1 2x≤−10 x≤−5 (قسمنا على 2 موجب، لم نعكس العلامة)
4. مجموعة الحل: x≥4 أو x≤−5.
   • التمثيل البياني: دائرة مغلقة عند 4 وسهم يتجه لليمين، ودائرة مغلقة عند -5 وسهم يتجه لليسار.
   • الترميز الفتري: (سالب ما لا نهاية، -5] اتحاد [4، موجب ما لا نهاية).

مثال 3: متباينة تتطلب عزل القيمة المطلقة أولًا

حل المتباينة: −2∣x+5∣+7<1

1. عزل تعبير القيمة المطلقة:
   • نطرح 7 من الطرفين: −2∣x+5∣<1−7 −2∣x+5∣<−6
   • نقسم على -2 (عدد سالب). نعكس علامة المتباينة. ∣x+5∣>3 (علامة < تحولت إلى >)
2. تحديد النوع والتحويل: أصبحت الآن “القيمة المطلقة أكبر من” عدد موجب (3)، لذا نحولها إلى متباينة مركبة بـ “أو”: x+5>3 أو x+5<−3
3. حل كل متباينة بسيطة:
   • الأولى: x+5>3 x>3−5 x>−2
   • الثانية: x+5<−3 x<−3−5 x<−8
4. مجموعة الحل: x>−2 أو x<−8.
   • التمثيل البياني: دائرة مفتوحة عند -2 وسهم يتجه لليمين، ودائرة مفتوحة عند -8 وسهم يتجه لليسار.
   • الترميز الفتري: (سالب ما لا نهاية، -8) اتحاد (-2، موجب ما لا نهاية).

تطبيقات المتباينات التي تتضمن القيمة المطلقة في الحياة الواقعية

تُعد المتباينات التي تتضمن القيمة المطلقة مفيدة بشكل خاص في نمذجة وتحديد النطاقات أو التفاوتات:

1. التحكم في الجودة والتصنيع: تحديد المواصفات المسموح بها للمنتج.
   • مثال: يجب أن يكون طول قطعة معينة 10 سنتيمترات مع هامش خطأ لا يزيد عن 0.1 سنتيمتر. يمكن التعبير عن ذلك كـ ∣L−10∣≤0.1 (حيث L هو الطول الفعلي)، مما يعني أن L يجب أن يكون بين 9.9 و 10.1 سنتيمتر.
2. الفيزياء والهندسة: تحديد نطاقات الأخطاء في القياسات أو درجات الحرارة.
   • مثال: إذا كانت درجة حرارة غرفة العمليات يجب أن تكون 20 درجة مئوية، مع هامش تفاوت بمقدار 2 درجة مئوية. يمكن التعبير عن ذلك كـ ∣T−20∣≤2 (حيث T هي درجة الحرارة).
3. الإحصاء والتحليل: في تحليل الانحرافات عن المتوسط أو القيم المتطرفة.
   • مثال: تحديد البيانات التي تنحرف عن متوسط معين بأكثر من قيمة محددة.
4. الملاحة وتحديد المواقع: تحديد نطاق المسافة من نقطة معينة.
   • مثال: لتكون ضمن منطقة تغطية شبكة معينة، يجب أن تكون على مسافة لا تزيد عن 5 كيلومترات من برج الإرسال.
5. المناخ والبيئة: تحديد نطاقات درجة الحرارة الآمنة للكائنات الحية.
   • مثال: قد يكون نوع من النباتات قادرًا على البقاء إذا كانت درجة الحرارة اليومية تختلف عن 25 درجة مئوية بأقل من 8 درجات.

الخاتمة

تُشكل المتباينات التي تتضمن القيمة المطلقة مرحلة متقدمة ومهمة في دراسة الجبر، حيث تُقدم طريقة قوية لوصف العلاقات المستندة إلى المسافة. إن القدرة على تحويل هذه المتباينات إلى متباينات مركبة من نوع “و” أو “أو” بناءً على اتجاه علامة المتباينة، مع الالتزام الصارم بقواعد عكس العلامة عند الضرب أو القسمة على الأعداد السالبة، هي جوهر إتقان هذه المهارة. لا تقتصر أهمية هذه المتباينات على التمارين الجبرية فحسب؛ بل تُعد أداة تحليلية أساسية في مجموعة واسعة من التطبيقات الواقعية، من التحكم في الجودة الصناعية إلى نمذجة الظواهر الطبيعية. تُعزز هذه المتباينات التفكير النقدي، وتُمكننا من فهم وتفسير القيود المعقدة التي تُحدد نطاقات القيم الممكنة، مما يُسهم في بناء أساس رياضي متين لمواجهة التحديات المستقبلية.