مقدمة

بعد استيعاب كيفية حل المتباينات باستخدام عمليتي الجمع والطرح، ننتقل إلى مستوى آخر من التعقيد والمرونة: حل المتباينات بالضرب أو القسمة. هذا النوع من المتباينات يفتح آفاقًا جديدة لوصف العلاقات اللامتساوية، حيث تتضمن هذه المرة معاملات مضروبة في المتغيرات أو مقسومة عليها. بينما تتشارك هذه العمليات مع الجمع والطرح في هدف عزل المتغير، إلا أن هناك قاعدة حاسمة ومميزة يجب مراعاتها عند الضرب أو القسمة على الأعداد السالبة، وهي ما يميز حل المتباينات عن حل المعادلات. إن إتقان هذه القاعدة ليس مجرد تفصيل رياضي، بل هو مفتاح لحل مجموعة واسعة من المشكلات في مجالات متنوعة، من تحديد التكاليف الحقيقية بناءً على نسبة معينة، إلى فهم القيود الفيزيائية في المعادلات التي تتضمن سرعة أو كثافة. يمثل هذا البحث دليلًا شاملًا لفهم المبادئ التي تحكم حل المتباينات بالضرب أو القسمة، مع التركيز على أهمية التفريق بين الأعداد الموجبة والسالبة لضمان دقة الحلول.

مراجعة سريعة للمتباينات ومفاهيمها الأساسية

قبل الغوص في تفاصيل الضرب والقسمة، دعنا نُذكر أنفسنا بالمفاهيم الأساسية للمتباينات:

المتباينة (Inequality): هي عببير رياضي يُقارن بين قيمتين أو تعبيرين باستخدام علامات عدم التساوي. على عكس المعادلة التي تُحدد قيمة واحدة (أو عدد محدود من القيم) للمتغير، تُحدد المتباينة مجموعة من القيم التي يمكن أن يتخذها المتغير.

علامات المتباينة:

• أصغر من (<): تعني أن القيمة اليسرى أقل من اليمنى. مثال: 5 < 8.
• أكبر من (>): تعني أن القيمة اليسرى أكبر من اليمنى. مثال: 10 > 3.
• أصغر من أو تساوي (≤): تعني أن القيمة اليسرى أقل من أو تساوي اليمنى. مثال: س ≤ 7.
• أكبر من أو تساوي (≥): تعني أن القيمة اليسرى أكبر من أو تساوي اليمنى. مثال: ص ≥ 2.
• لا يساوي (≠): تعني أن القيمتين ليستا متساويتين. مثال: س ≠ 4.

حل المتباينة: هو مجموعة كل القيم التي يمكن أن يأخذها المتغير لجعل المتباينة صحيحة. عادة ما تُمثل مجموعة الحل على خط الأعداد أو باستخدام الترميز الفتري.

الخصائص الأساسية لعمليتي الضرب والقسمة في المتباينات

يكمن الاختلاف الجوهري بين حل المعادلات والمتباينات في التعامل مع الضرب والقسمة على الأعداد السالبة.

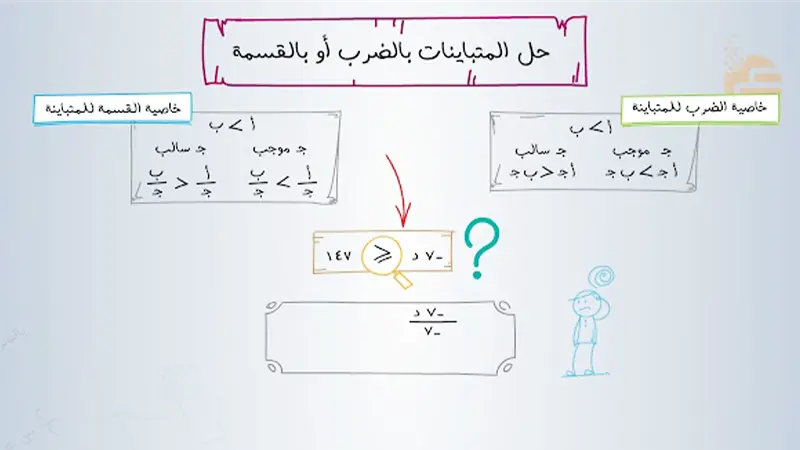
1. خاصية الضرب (للأعداد الموجبة): إذا ضربنا كلا طرفي المتباينة في نفس الكمية الموجبة، فإن اتجاه علامة المتباينة لا يتغير.
   • إذا كان أ < ب و ج > 0، فإن أ مضروبًا في جـ < ب مضروبًا في جـ.
   • مثال: إذا كان 2 < 4، وضربنا الطرفين في 3: 2 مضروبًا في 3 < 4 مضروبًا في 3 6 < 12 (صحيح).
2. خاصية القسمة (للأعداد الموجبة): إذا قسمنا كلا طرفي المتباينة على نفس الكمية الموجبة، فإن اتجاه علامة المتباينة لا يتغير.
   • إذا كان أ > ب و ج > 0، فإن أ مقسومًا على جـ > ب مقسومًا على جـ.
   • مثال: إذا كان 10 > 5، وقسمنا الطرفين على 5: 10 مقسومًا على 5 > 5 مقسومًا على 5 2 > 1 (صحيح).
3. خاصية الضرب (للأعداد السالبة): إذا ضربنا كلا طرفي المتباينة في نفس الكمية السالبة، فإن اتجاه علامة المتباينة ينعكس.
   • إذا كان أ < ب و ج < 0، فإن أ مضروبًا في جـ > ب مضروبًا في جـ. (لاحظ أن علامة < تحولت إلى >)
   • مثال: إذا كان 2 < 4، وضربنا الطرفين في سالب 3: 2 مضروبًا في سالب 3 هو سالب 6. 4 مضروبًا في سالب 3 هو سالب 12. الآن، يجب أن نعكس العلامة لتصبح: سالب 6 > سالب 12 (صحيح).
4. خاصية القسمة (للأعداد السالبة): إذا قسمنا كلا طرفي المتباينة على نفس الكمية السالبة، فإن اتجاه علامة المتباينة ينعكس.
   • إذا كان أ > ب و ج < 0، فإن أ مقسومًا على جـ < ب مقسومًا على جـ. (لاحظ أن علامة > تحولت إلى <)
   • مثال: إذا كان 10 > سالب 2، وقسمنا الطرفين على سالب 2: 10 مقسومًا على سالب 2 هو سالب 5. سالب 2 مقسومًا على سالب 2 هو 1. الآن، يجب أن نعكس العلامة لتصبح: سالب 5 < 1 (صحيح).

هذه القاعدة (عكس علامة المتباينة عند الضرب أو القسمة على عدد سالب) هي الأهم والأكثر شيوعًا للخطأ في حل المتباينات.

خطوات حل المتباينات بالضرب أو القسمة

الهدف الأساسي هو عزل المتغير في أحد طرفي المتباينة.

1. تحديد العملية التي تربط المتغير بالعدد الثابت: هل المتغير مضروب في عدد، أم مقسوم على عدد؟
2. تطبيق العملية العكسية:
   • إذا كان المتغير مضروبًا في عدد، قم بقسمة كلا طرفي المتباينة على هذا العدد.
   • إذا كان المتغير مقسومًا على عدد، قم بضرب كلا طرفي المتباينة في هذا العدد.
3. الانتباه لإشارة العدد:
   • إذا كان العدد الذي تضربه أو تقسم عليه موجبًا، فحافظ على اتجاه علامة المتباينة كما هي.
   • إذا كان العدد الذي تضربه أو تقسم عليه سالبًا، فاعكس اتجاه علامة المتباينة.

أمثلة توضيحية:

مثال 1: حل متباينة بالقسمة على عدد موجب

حل المتباينة: 4 س أكبر من أو تساوي 20

1. المتغير س مضروب في 4.
2. نقسم كلا الطرفين على 4 (عدد موجب). 4 س مقسومًا على 4 أكبر من أو تساوي 20 مقسومًا على 4 س أكبر من أو تساوي 5
3. مجموعة الحل: جميع الأعداد التي هي أكبر من أو تساوي 5.
   • التمثيل البياني: دائرة مغلقة عند 5، وسهم يتجه إلى اليمين.
   • الترميز الفتري: [5، موجب ما لا نهاية).

مثال 2: حل متباينة بالضرب في عدد موجب

حل المتباينة: س مقسومًا على 3 أصغر من 7

1. المتغير س مقسوم على 3.
2. نضرب كلا الطرفين في 3 (عدد موجب). س مقسومًا على 3 مضروبًا في 3 أصغر من 7 مضروبًا في 3 س أصغر من 21
3. مجموعة الحل: جميع الأعداد التي هي أصغر من 21.
   • التمثيل البياني: دائرة مفتوحة عند 21، وسهم يتجه إلى اليسار.
   • الترميز الفتري: (سالب ما لا نهاية، 21).

مثال 3: حل متباينة بالقسمة على عدد سالب (هام)

حل المتباينة: سالب 2 س أكبر من 10

1. المتغير س مضروب في سالب 2.
2. نقسم كلا الطرفين على سالب 2 (عدد سالب). هنا يجب عكس اتجاه المتباينة. سالب 2 س مقسومًا على سالب 2 أصغر من 10 مقسومًا على سالب 2 س أصغر من سالب 5
3. مجموعة الحل: جميع الأعداد التي هي أصغر من سالب 5.
   • التمثيل البياني: دائرة مفتوحة عند سالب 5، وسهم يتجه إلى اليسار.
   • الترميز الفتري: (سالب ما لا نهاية، سالب 5).

مثال 4: حل متباينة بالضرب في عدد سالب (هام)

حل المتباينة: س مقسومًا على سالب 4 أصغر من أو تساوي 3

1. المتغير س مقسوم على سالب 4.
2. نضرب كلا الطرفين في سالب 4 (عدد سالب). هنا يجب عكس اتجاه المتباينة. س مقسومًا على سالب 4 مضروبًا في سالب 4 أكبر من أو تساوي 3 مضروبًا في سالب 4 س أكبر من أو تساوي سالب 12
3. مجموعة الحل: جميع الأعداد التي هي أكبر من أو تساوي سالب 12.
   • التمثيل البياني: دائرة مغلقة عند سالب 12، وسهم يتجه إلى اليمين.
   • الترميز الفتري: [سالب 12، موجب ما لا نهاية).

تمثيل مجموعة الحل على خط الأعداد (تأكيد)

يظل التمثيل البياني على خط الأعداد هو أفضل طريقة مرئية لعرض نطاق الحل:

• دائرة مفتوحة (غير مظللة): للعلامات < و > (العدد ليس جزءًا من الحل).
• دائرة مغلقة (مظللة): للعلامات ≤ و ≥ (العدد جزء من الحل).
• اتجاه السهم: لليمين للأعداد الأكبر، ولليسار للأعداد الأصغر.

تطبيقات المتباينات في الحياة الواقعية

المتباينات التي تتضمن الضرب أو القسمة تُستخدم لوصف قيود معقدة في العديد من السيناريوهات:

المعدلات والنسب: حساب القيم القصوى أو الدنيا بناءً على معدل معين.

• مثال: إذا كنت تستطيع قراءة 50 صفحة في الساعة، وتريد أن تقرأ كتابًا فيه 300 صفحة، فكم ساعة (س) ستحتاج؟ 50 مضروبًا في س أكبر من أو تساوي 300. س أكبر من أو تساوي 6. ستحتاج 6 ساعات أو أكثر.

التكاليف والخصومات: تحديد الكميات التي يمكن شراؤها بناءً على المكاسب أو الخسائر النسبية.

• مثال: إذا كان تخفيض بنسبة 25 بالمائة (0.25) على سعر سلعة (س) يجعل سعرها الجديد أقل من 15 دولارًا: س ناقص 0.25 س أصغر من 15 0.75 س أصغر من 15 س أصغر من 15 مقسومًا على 0.75 س أصغر من 20. يجب أن يكون السعر الأصلي أقل من 20 دولارًا.

المتوسطات والدرجات: حساب الدرجات الدنيا المطلوبة للحصول على متوسط معين.

• مثال: يجب أن يكون متوسط درجاتك (د) في 4 اختبارات أكبر من أو يساوي 80 لتجتاز الدورة. إذا كانت درجاتك في الاختبارات الثلاثة الأولى هي 70 و 75 و 85، فما هي أقل درجة تحتاجها في الاختبار الرابع (خ)؟ (70 زائد 75 زائد 85 زائد خ) مقسومًا على 4 أكبر من أو تساوي 80. (230 زائد خ) مقسومًا على 4 أكبر من أو تساوي 80. 230 زائد خ أكبر من أو تساوي 320. خ أكبر من أو تساوي 90. تحتاج 90 أو أكثر في الاختبار الأخير.

الهندسة والقياسات: تحديد أبعاد الأشكال بناءً على قيود المساحة أو الحجم.

• مثال: إذا كانت مساحة مستطيل (طوله 10) يجب أن تكون أقل من 50 وحدة مربعة، فما هو أقصى عرض (ع) له؟ 10 مضروبًا في ع أصغر من 50. ع أصغر من 5. يجب أن يكون العرض أقل من 5 وحدات.

الخاتمة

تُعد القدرة على حل المتباينات بالضرب أو القسمة مهارة محورية في الجبر، تُمكّننا من تحليل العلاقات اللامتساوية التي تتضمن عمليات الضرب والقسمة. إن فهم القاعدة الأساسية المتعلقة بعكس علامة المتباينة عند الضرب أو القسمة على عدد سالب هو مفتاح الدقة في هذه العملية. هذه المهارة لا تقتصر على حل التمارين الأكاديمية فحسب، بل تُقدم لنا أداة قوية لوصف القيود، وتحديد النطاقات، واتخاذ قرارات مستنيرة في سياقات واقعية متعددة، من التخطيط المالي إلى التحليل الهندسي. إن إتقان هذه المتباينات يُعزز من قدرتنا على التفكير النقدي، ويُمهد الطريق لفهم أعمق للمفاهيم الرياضية الأكثر تعقيدًا، مما يُسهم في بناء أساس رياضي متين لمواجهة التحديات المستقبلية.