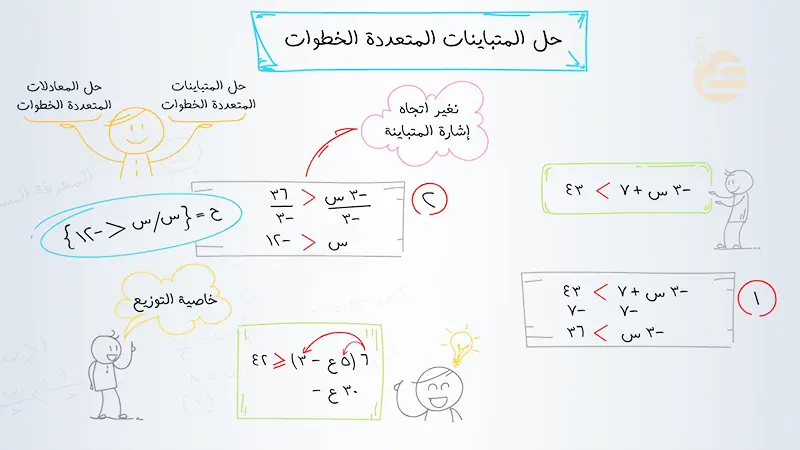
مقدمة

في مسيرة تعلم الجبر، تُشكل المتباينات المتعددة الخطوات (Multi-Step Inequalities) التحدي الطبيعي التالي بعد إتقان المتباينات ذات الخطوة الواحدة. هذه المتباينات، التي تتضمن أكثر من عملية رياضية واحدة، تُقدم سيناريوهات أكثر واقعية تُعبر عن قيود مركبة، حيث لا تكون العلاقة بين الكميات مجرد مقارنة بسيطة، بل تتضمن تداخلات من الجمع والطرح والضرب والقسمة والتوزيع. إن القدرة على حل هذه المتباينات تُعد مهارة أساسية تُمكننا من تحديد مجموعات القيم التي تُرضي شروطًا متعددة في آن واحد. هذا البحث سيُفصل المبادئ والخطوات المنهجية اللازمة لفك شفرة هذه المتباينات المعقدة، مع التأكيد على القواعد الحاسمة التي تُفرق بينها وبين المعادلات، خاصة عند التعامل مع الأعداد السالبة. إن إتقان حل المتباينات المتعددة الخطوات يُعزز التفكير التحليلي، ويُجهز الطلاب لمعالجة مشكلات رياضية وعلمية وهندسية أكثر تعقيدًا تتطلب فهمًا عميقًا للعلاقات اللامتساوية.

مراجعة سريعة للمتباينات ومفاهيمها الأساسية

قبل الغوص في المتباينات المتعددة الخطوات، من المهم استعراض المبادئ الأساسية للمتباينات بشكل عام:

المتباينة (Inequality): عبارة رياضية تُقارن بين قيمتين أو تعبيرين باستخدام إحدى علامات عدم التساوي. على عكس المعادلات التي تبحث عن قيمة محددة للمتغير، تُحدد المتباينات نطاقًا من القيم.

علامات المتباينة:

• أصغر من (<): تعني أن القيمة اليسرى أقل من القيمة اليمنى.
• أكبر من (>): تعني أن القيمة اليسرى أكبر من القيمة اليمنى.
• أصغر من أو تساوي (≤): تعني أن القيمة اليسرى أقل من أو تساوي القيمة اليمنى.
• أكبر من أو تساوي (≥): تعني أن القيمة اليسرى أكبر من أو تساوي القيمة اليمنى.

حل المتباينة: هو مجموعة كل القيم التي يُمكن أن يتخذها المتغير لجعل المتباينة صحيحة. تُمثل مجموعة الحل غالبًا على خط الأعداد أو باستخدام الترميز الفتري.

الخصائص الأساسية للعمليات على المتباينات (مراجعة وتأكيد)

تُطبق على المتباينات نفس العمليات الجبرية التي تُطبق على المعادلات، ولكن مع قاعدة حاسمة تخص الضرب والقسمة على الأعداد السالبة.

خاصية الإضافة والطرح: إذا أضفنا أو طرحنا نفس الكمية من كلا طرفي المتباينة، فإن اتجاه علامة المتباينة لا يتغير.

• مثال: إذا كان س زائد 3 أكبر من 7، فإن س زائد 3 ناقص 3 أكبر من 7 ناقص 3، أي س أكبر من 4.

خاصية الضرب والقسمة على عدد موجب: إذا ضربنا أو قسمنا كلا طرفي المتباينة على نفس الكمية الموجبة، فإن اتجاه علامة المتباينة لا يتغير.

• مثال: إذا كان 2س أصغر من 10، فإن 2س مقسومًا على 2 أصغر من 10 مقسومًا على 2، أي س أصغر من 5.

خاصية الضرب والقسمة على عدد سالب: إذا ضربنا أو قسمنا كلا طرفي المتباينة على نفس الكمية السالبة، فإن اتجاه علامة المتباينة ينعكس.

• مثال: إذا كان سالب 3س أصغر من 12، فإن سالب 3س مقسومًا على سالب 3 أكبر من 12 مقسومًا على سالب 3، أي س أكبر من سالب 4.
• هذه القاعدة هي الأهم والأكثر شيوعًا للخطأ في حل المتباينات. يجب الانتباه جيدًا لإشارة العدد الذي يتم به الضرب أو القسمة.

خطوات حل المتباينات المتعددة الخطوات

يشبه حل المتباينات المتعددة الخطوات حل المعادلات المتعددة الخطوات، ولكن مع الانتباه المستمر لعلامة المتباينة وتغيير اتجاهها عند الضرورة. الهدف هو عزل المتغير في أحد طرفي المتباينة.

النهج المنهجي (تتبع نفس ترتيب حل المعادلات، مع الانتباه لإشارة الضرب والقسمة):

1. تبسيط كل طرف من أطراف المتباينة (إن وجد):
   • تطبيق خاصية التوزيع: إذا كان هناك رقم أو متغير مضروبًا في قوسين، قم بتوزيع الضرب على الحدود داخل القوسين.
   • تجميع الحدود المتشابهة: اجمع أي حدود متشابهة في نفس الطرف من المتباينة.
   • مثال: 5س زائد 8 ناقص 2س أكبر من 20 نجمع الحدود المتشابهة: 3س زائد 8 أكبر من 20.
2. نقل الحدود الثابتة (الأرقام) إلى جانب واحد من المتباينة:
   • استخدم العملية العكسية للتخلص من أي ثوابت موجودة في نفس طرف المتغير. إذا كانت مضافة، اطرحها. إذا كانت مطروحة، اجمعها. افعل ذلك على كلا الطرفين.
   • مثال: 3س زائد 8 أكبر من 20 نطرح 8 من كلا الطرفين: 3س زائد 8 ناقص 8 أكبر من 20 ناقص 8 3س أكبر من 12.
3. نقل المتغيرات إلى جانب واحد من المتباينة (إذا كانت موجودة في كلا الطرفين):
   • إذا كان المتغير موجودًا في كلا طرفي المتباينة، انقل جميع الحدود التي تحتوي على المتغير إلى طرف واحد، عادةً الطرف الأيسر. استخدم عمليات الجمع أو الطرح.
   • مثال: 5س ناقص 3 أصغر من 2س زائد 9 نطرح 2س من كلا الطرفين: 5س ناقص 2س ناقص 3 أصغر من 2س ناقص 2س زائد 9 3س ناقص 3 أصغر من9.
4. عزل المتغير (التخلص من المعامل):
   • استخدم العملية العكسية للتخلص من المعامل (العدد المضروب في المتغير).
   • إذا كان المعامل مضروبًا، اقسم كلا الطرفين عليه.
   • إذا كان المعامل مقسومًا، اضرب كلا الطرفين فيه.
   • تذكر القاعدة الذهبية: إذا كان العدد الذي تقسم أو تضرب عليه سالبًا، اعكس اتجاه علامة المتباينة.
   • مثال: 3س أكبر من 12 نقسم كلا الطرفين على 3 (موجب): 3س مقسومًا على 3 أكبر من 12 مقسومًا على 3 س أكبر من 4.
5. التحقق من الحل (اختياري ولكن موصى به):
   • اختر قيمة واحدة تقع ضمن مجموعة الحل التي حصلت عليها وعوضها في المتباينة الأصلية.
   • اختر قيمة واحدة لا تقع ضمن مجموعة الحل وعوضها في المتباينة الأصلية.
   • يجب أن تجعل القيمة الأولى المتباينة صحيحة، بينما تجعل القيمة الثانية المتباينة خاطئة.
   • مثال: إذا كان الحل س أكبر من 4، اختر 5 (صحيح) و 3 (خطأ).

أمثلة تطبيقية متنوعة على حل المتباينات المتعددة الخطوات

دعونا نطبق هذه الخطوات على أمثلة أكثر تعقيدًا:

مثال 1: متباينة تتضمن توزيعًا وجمعًا

حل المتباينة: 2 مضروبًا في (س زائد 3) ناقص 5 أكبر من أو تساوي 15

1. تبسيط الطرف الأيسر (توزيع): 2س زائد 6 ناقص 5 أكبر من أو تساوي 15 2س زائد 1 أكبر من أو تساوي 15
2. نقل الحدود الثابتة: نطرح 1 من كلا الطرفين: 2س زائد 1 ناقص 1 أكبر من أو تساوي 15 ناقص 1 2س أكبر من أو تساوي 14
3. عزل المتغير: نقسم على 2 (عدد موجب): 2س مقسومًا على 2 أكبر من أو تساوي 14 مقسومًا على 2 س أكبر من أو تساوي 7
4. مجموعة الحل: س أكبر من أو تساوي 7.
   • التمثيل البياني: دائرة مغلقة عند 7، وسهم يتجه لليمين.

مثال 2: متباينة تتضمن متغيرات في كلا الطرفين ومعامل سالب

حل المتباينة: 7 ناقص 4س أصغر من 3س زائد 21

1. تبسيط الأطراف: لا يوجد تبسيط أولي.
2. نقل المتغيرات إلى جانب واحد: (يمكن نقل 4س إلى اليمين لتجنب المعامل السالب مؤقتًا، أو نقل 3س إلى اليسار) لنقل 3س إلى اليسار: نطرح 3س من كلا الطرفين. 7 ناقص 4س ناقص 3س أصغر من 3س ناقص 3س زائد 21 7 ناقص 7س أصغر من 21
3. نقل الحدود الثابتة: نطرح 7 من كلا الطرفين: 7 ناقص 7 ناقص 7س أصغر من 21 ناقص 7 سالب 7س أصغر من 14
4. عزل المتغير (قسمة على سالب): نقسم على سالب 7 (عدد سالب). نعكس علامة المتباينة. سالب 7س مقسومًا على سالب 7 أكبر من 14 مقسومًا على سالب 7 س أكبر من سالب 2
5. مجموعة الحل: س أكبر من سالب 2.
   • التمثيل البياني: دائرة مفتوحة عند سالب 2، وسهم يتجه لليمين.

تطبيقات المتباينات المتعددة الخطوات في الحياة الواقعية

المتباينات المتعددة الخطوات قوية جدًا في نمذجة وحل المشكلات التي تتضمن شروطًا متعددة أو قيودًا معقدة:

1. الخطط المالية والميزانيات: تحديد الدخل المطلوب لتحقيق هدف مالي معين بعد خصم النفقات الثابتة والمتغيرة.
   • مثال: تريد شركة أن يكون صافي ربحها الشهري (بعد خصم المصاريف الثابتة 5000 دولار و 25 بالمائة من الإيرادات كمصاريف تشغيل) أكبر من 10000 دولار. إذا كانت الإيرادات الشهرية هي (إ)، فما هو الحد الأدنى للإيرادات؟ إ ناقص 5000 ناقص 0.25 إ أكبر من 10000 0.75 إ ناقص 5000 أكبر من 10000 0.75 إ أكبر من 15000 إ أكبر من 15000 مقسومًا على 0.75 إ أكبر من 20000 دولار.
2. تخطيط المشاريع والأعمال: تحديد عدد الموارد أو الساعات اللازمة لإكمال مشروع ضمن قيود زمنية أو ميزانية.
   • مثال: تحتاج إلى إنتاج 500 قطعة. تنتج الآلة أ 20 قطعة في الساعة، والآلة ب 15 قطعة في الساعة. إذا عملت الآلة أ لمدة 10 ساعات، فكم ساعة (س) يجب أن تعمل الآلة ب لإنتاج 500 قطعة على الأقل؟ (20 مضروبًا في 10) زائد (15 مضروبًا في س) أكبر من أو تساوي 500 200 زائد 15س أكبر من أو تساوي 500 15س أكبر من أو تساوي 300 س أكبر من أو تساوي 20 ساعة.
3. الفيزياء والهندسة: تحليل الأنظمة التي تخضع لقوى أو شروط متعددة.
   • مثال: يجب أن تكون سرعة سيارة (ع) زائد سرعة الرياح (ر) أقل من سرعة قصوى معينة.
4. الصحة والتغذية: حساب احتياجات السعرات الحرارية أو العناصر الغذائية مع الأخذ في الاعتبار مستويات النشاط المختلفة.
   • مثال: حساب الحد الأقصى لعدد الوجبات الخفيفة التي يمكن تناولها مع الحفاظ على إجمالي السعرات الحرارية اليومية ضمن حد معين بعد تناول الوجبات الرئيسية.
5. تحديد النطاقات المسموح بها: تحديد القيم المسموح بها لمتغير ما في سيناريو معين، مثل نطاق درجة حرارة التشغيل الآمن لجهاز كهربائي.

الخاتمة

تُعد المتباينات المتعددة الخطوات تجسيدًا للعلاقات المعقدة التي تُصادفنا في الرياضيات والعالم الحقيقي. إن إتقان منهجية حلها، بدءًا من تبسيط الأطراف، مرورًا بنقل الحدود، وصولًا إلى عزل المتغير مع الانتباه الحاسم لقاعدة عكس علامة المتباينة عند الضرب أو القسمة على عدد سالب، هو مهارة جوهرية. لا تقتصر أهمية هذه المتباينات على قدرتها على حل المسائل الجبرية فحسب، بل تُعزز أيضًا التفكير النقدي والتحليلي، مما يُمكننا من فهم القيود، وتحديد النطاقات المحتملة، واتخاذ القرارات في مواقف الحياة اليومية والعلمية التي تتطلب فهمًا عميقًا للعلاقات اللامتساوية. تُشكل المتباينات المتعددة الخطوات خطوة متقدمة في رحلة تعلم الجبر، وتُعد أساسًا لبناء نماذج رياضية أكثر تعقيدًا في المستقبل.