مقدمة

يُعتبر التماثل مفهومًا جوهريًا وعميقًا في عالم الرياضيات، فهو ليس مجرد خاصية بصرية للأشكال الهندسية، بل هو مبدأ أساسي يربط بين مختلف فروع الرياضيات ويكشف عن أنماط ونظم خفية. التماثل في الرياضيات يشير إلى خاصية بقاء الكائن الرياضي (سواء كان شكلًا هندسيًا أو معادلة جبرية أو دالة رياضية أو غير ذلك) دون تغيير تحت تحويل معين. هذا المفهوم متعدد الأوجه يلعب دورًا حاسمًا في فهم البنية الداخلية للرياضيات وتطبيقاتها في العلوم المختلفة.

التماثل في الهندسة

يُعد التماثل في الهندسة من أولى وأبرز مظاهر هذا المفهوم في الرياضيات. هناك عدة أنواع من التماثل الهندسي:

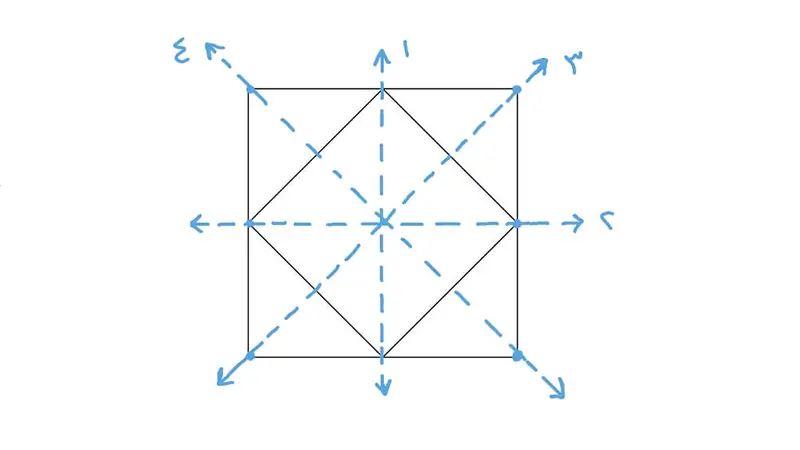
1. التماثل الانعكاسي (Reflectional Symmetry): يحدث عندما يمكن تقسيم شكل هندسي بخط مستقيم (محور التماثل) إلى نصفين متطابقين تمامًا، بحيث يكون كل نصف صورة معكوسة للآخر. أمثلة:
   • المستقيم: له عدد لا نهائي من محاور التماثل.
   • الزاوية: لها محور تماثل واحد ينصفها.
   • المضلعات المنتظمة: لها عدد من محاور التماثل يساوي عدد أضلاعها (المربع له 4، الخماسي المنتظم له 5، وهكذا).
   • الدائرة: لها عدد لا نهائي من محاور التماثل تمر بمركزها.
   • القطوع المخروطية: القطع الناقص والقطع الزائد والمكافئ لها محاور تماثل محددة.
2. التماثل الدوراني (Rotational Symmetry): يحدث عندما يمكن تدوير شكل هندسي حول نقطة مركزية بزاوية أقل من 360 درجة بحيث ينطبق الشكل على نفسه. أمثلة:
   • الدائرة: لها تماثل دوراني لأي زاوية حول مركزها.
   • المضلعات المنتظمة: لها تماثل دوراني بزوايا تساوي 360 درجة مقسومة على عدد الأضلاع (المربع له تماثل دوراني بزوايا 90، 180، 270 درجة).
3. التماثل الانتقالي (Translational Symmetry): يحدث في الأنماط والتراكيب التي تتكرر بشكل منتظم في اتجاه معين. أمثلة:
   • تبليط المستويات: الأنماط المتكررة التي تغطي سطحًا مستويًا دون فراغات أو تداخلات.
   • شبكات الكريستال: الترتيب المنتظم للذرات في المواد الصلبة.
4. التماثل النقطي (Point Symmetry): يحدث عندما يمكن تدوير شكل هندسي بزاوية 180 درجة حول نقطة مركزية بحيث ينطبق الشكل على نفسه. هذا يكافئ وجود نقطة مركزية بحيث أن لكل نقطة في الشكل توجد نقطة أخرى مقابلة لها تبعد نفس المسافة عن المركز وفي الاتجاه المعاكس. أمثلة:
   • الدائرة: لها تماثل نقطي حول مركزها.
   • متوازي الأضلاع: له تماثل نقطي حول نقطة تقاطع قطريه.
5. التماثل الانزلاقي (Glide Reflection Symmetry): هو تركيب لانعكاس حول مستقيم مع إزاحة على طول نفس المستقيم. يظهر هذا النوع من التماثل في بعض الأنماط والزخارف.

التماثل في الجبر

يظهر التماثل أيضًا في الجبر في سياقات مختلفة:

1. المعادلات والتعبيرات المتماثلة: يُقال أن معادلة أو تعبير جبري متماثل إذا بقي دون تغيير عند تبديل المتغيرات فيما بينها. أمثلة:
   • س + ص = ص + س
   • س ص = ص س
   • س² + ص² + ع² تلعب هذه التعبيرات والمعادلات دورًا مهمًا في حل أنظمة المعادلات وفي نظرية كثيرات الحدود.
2. الدوال المتماثلة: هي دوال لا تتغير قيمتها عند تبديل مدخلاتها. مثال: الدالة f(س، ص) = س² + ص² هي دالة متماثلة لأن f(س، ص) = f(ص، س). الدوال المتماثلة لها تطبيقات في الجبر والتوافقيات.

التماثل في التحليل الرياضي

يظهر التماثل في التحليل الرياضي في سياق الدوال والرسوم البيانية:

1. الدوال الزوجية والفردية:
   • الدالة الزوجية: هي دالة تحقق الشرط f(س) = f(-س)، ويكون تمثيلها البياني متماثلًا حول محور الصادات. مثال: f(س) = س².
   • الدالة الفردية: هي دالة تحقق الشرط f(س) = -f(-س)، ويكون تمثيلها البياني متماثلًا حول نقطة الأصل. مثال: f(س) = س³. يساعد تحديد زوجية أو فردية الدالة في دراسة خصائصها وتكاملها.

التماثل في نظرية الأعداد

يظهر التماثل أيضًا في بعض المفاهيم في نظرية الأعداد:

1. الأعداد المتناظرة: بعض المتتاليات أو المجموعات من الأعداد تظهر خصائص متماثلة.
2. الأعداد القليدية (Palindromic Numbers): هي الأعداد التي تقرأ نفسها من اليمين إلى اليسار ومن اليسار إلى اليمين (مثل 121).

التماثل في الجبر المجرد (نظرية الزمر)

يُعتبر مفهوم التماثل أساسيًا في فرع الجبر المجرد المعروف باسم نظرية الزمر.

1. زمرة التماثل (Symmetry Group): هي مجموعة تتكون من جميع التحويلات التي تحافظ على شكل أو بنية كائن رياضي معين (مثل مضلع منتظم أو شكل ثلاثي الأبعاد)، مع عملية التركيب بين التحويلات كعملية الزمرة.
   • الزمرة الثنائية (Dihedral Group): هي زمرة التماثل لمضلع منتظم ذي نون ضلعًا، وتشمل الدورانات والانعكاسات التي تحافظ على شكل المضلع.
   • الزمرة الدورية (Cyclic Group): هي زمرة التماثل الدوراني لشكل ما.

تلعب نظرية الزمر دورًا حاسمًا في فهم التماثل في الرياضيات والفيزياء والكيمياء.

تطبيقات التماثل في الرياضيات

للتماثل تطبيقات واسعة في مختلف فروع الرياضيات:

1. حل المشكلات: يمكن استخدام التماثل لتبسيط المشكلات الرياضية وإيجاد حلول أسهل. على سبيل المثال، عند حساب مساحة منطقة متماثلة، قد يكون من الأسهل حساب مساحة نصف المنطقة ثم مضاعفتها.
2. تصنيف الكائنات الرياضية: يُستخدم التماثل لتصنيف الأشكال الهندسية والأنماط والهياكل الجبرية. على سبيل المثال، يمكن تصنيف المثلثات بناءً على أنواع التماثل التي تمتلكها (متساوي الأضلاع، متساوي الساقين، مختلف الأضلاع).
3. تطوير النظريات: مبادئ التماثل قادت إلى تطوير العديد من النظريات الرياضية الهامة.

خاتمة

التماثل ليس مجرد مفهوم بصري، بل هو مبدأ رياضي عميق يتجلى في مختلف فروع الرياضيات. لقد استعرضنا في هذا البحث مظاهر التماثل في الهندسة والجبر والتحليل الرياضي ونظرية الأعداد والجبر المجرد، بالإضافة إلى تطبيقاته المتنوعة في حل المشكلات وتطوير النظريات الرياضية. إن فهم التماثل يكشف عن البنية الداخلية للرياضيات ويبرز الترابط بين فروعها المختلفة. إنه مبدأ يوحد الأفكار ويضفي جمالًا وأناقة على الصرح الرياضي، ويؤكد على أن النظام والترتيب هما أساس الكون الرياضي الذي نسعى لفهمه واستكشافه.