المعادلات ذات الخطوتين
مقدمة
في عالم الجبر، تمثل المعادلات أدوات قوية للتعبير عن العلاقات بين الكميات وحل المشكلات التي تتضمن قيمًا مجهولة. تُعد المعادلات ذات الخطوتين نقطة انطلاق أساسية في رحلة تعلم حل المعادلات الجبرية، حيث تمثل مستوى بسيطًا ولكنه حاسم يربط بين المعادلات ذات الخطوة الواحدة والمعادلات الأكثر تعقيدًا. تتكون المعادلة ذات الخطوتين من متغير واحد يتطلب إجراء عمليتين حسابيتين (مثل الجمع والطرح، أو الضرب والقسمة، أو مزيج منهما) لعزله وإيجاد قيمته التي تحقق المساواة. إن فهم مفهوم المعادلة ذات الخطوتين ومكوناتها، واستيعاب الاستراتيجية الأساسية لحلها باستخدام العمليات العكسية، وإدراك أهميتها في بناء الفهم الجبري وتطبيق المفاهيم في حل المسائل الكلامية في الرياضيات والعلوم، يمثل أساسًا ضروريًا للتقدم في دراسة الجبر وتطبيقاته.
مفهوم المعادلة ذات الخطوتين ومكوناتها الأساسية
مفهوم المعادلة ذات الخطوتين (Two-Step Equation): هي معادلة جبرية تحتوي على متغير واحد ويتطلب حلها إجراء عمليتين حسابيتين لعزل المتغير وإيجاد قيمته التي تجعل طرفي المعادلة متساويين. غالبًا ما تتضمن هذه العمليتين مزيجًا من الجمع أو الطرح مع الضرب أو القسمة.
مكونات المعادلة ذات الخطوتين:
- المتغير (Variable): هو رمز (عادةً حرف مثل x، y، a) يمثل قيمة مجهولة نسعى لإيجادها.
- الثوابت (Constants): هي قيم عددية معروفة في المعادلة.
- المعامل (Coefficient): هو الرقم الذي يضرب المتغير. قد يكون المعامل ضمن إحدى العمليتين المطلوبتين للحل.
- العمليات الحسابية: تتضمن المعادلة ذات الخطوتين عمليتين حسابيتين على الأقل تؤثران على المتغير، مثل:
- الجمع والطرح (+، -)
- الضرب والقسمة (×، ÷، ·، /)
أمثلة على المعادلات ذات الخطوتين:
- 2x+3=7 (تتطلب الطرح ثم القسمة)
- 4y−1=5 (تتطلب الجمع ثم الضرب)
- −3a+6=−9 (تتطلب الطرح ثم القسمة)
- 5−2b=10 (تتطلب الطرح ثم الضرب في عدد سالب)
استراتيجيات حل المعادلات ذات الخطوتين باستخدام العمليات العكسية
تعتمد الاستراتيجية الأساسية لحل المعادلات ذات الخطوتين على استخدام العمليات العكسية (Inverse Operations) لعزل المتغير تدريجيًا. العملية العكسية هي العملية التي “تلغي” تأثير العملية الأصلية. فيما يلي العمليات العكسية الأساسية:
- عكس الجمع هو الطرح.
- عكس الطرح هو الجمع.
- عكس الضرب هو القسمة.
- عكس القسمة هو الضرب.
ترتيب العمليات العكسية: عند حل معادلة ذات خطوتين، نقوم بعكس ترتيب العمليات التي أُجريت على المتغير. عادةً ما نبدأ بعكس عمليتي الجمع أو الطرح الموجودتين في المعادلة، ثم نعكس عمليتي الضرب أو القسمة.
خطوات حل معادلة ذات الخطوتين:
- تحديد العمليات المؤثرة على المتغير: حدد العمليتين الحسابيتين اللتين تم إجراؤهما على المتغير في المعادلة.
- عكس عملية الجمع أو الطرح: استخدم العملية العكسية لعملية الجمع أو الطرح الموجودة في المعادلة للتخلص من الثابت الموجود بجانب الحد الذي يحتوي على المتغير. يجب تطبيق العملية نفسها على طرفي المعادلة للحفاظ على المساواة.
- عكس عملية الضرب أو القسمة: استخدم العملية العكسية لعملية الضرب أو القسمة الموجودة في المعادلة لعزل المتغير تمامًا. يجب تطبيق العملية نفسها على طرفي المعادلة للحفاظ على المساواة.
- التحقق من الحل: بعد إيجاد قيمة المتغير، قم بتعويض هذه القيمة في المعادلة الأصلية للتأكد من أن طرفي المعادلة متساويان.
أمثلة توضيحية لحل المعادلات ذات الخطوتين:
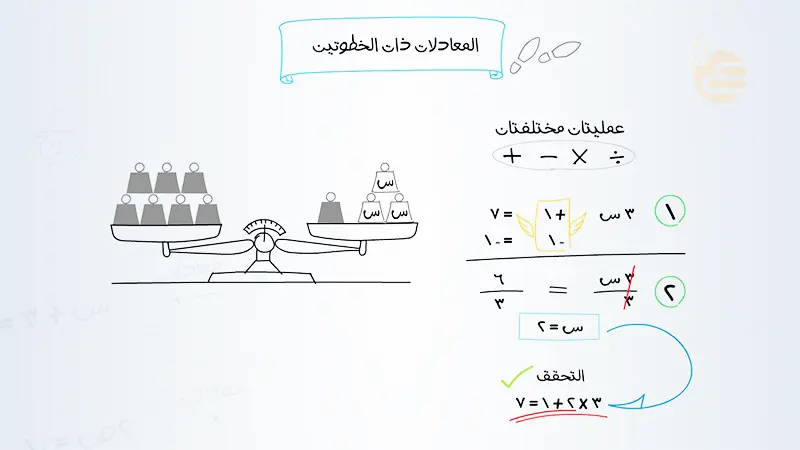
- حل المعادلة 2x+3=7:
- العمليات المؤثرة على x: الضرب في 2 ثم الجمع مع 3.
- عكس الجمع: اطرح 3 من طرفي المعادلة: 2x+3−3=7−3⟹2x=4.
- عكس الضرب: اقسم طرفي المعادلة على 2: 22x=24⟹x=2.
- التحقق: 2(2)+3=4+3=7 (الحل صحيح).
- حل المعادلة 4y−1=5:
- العمليات المؤثرة على y: القسمة على 4 ثم الطرح 1.
- عكس الطرح: اجمع 1 إلى طرفي المعادلة: 4y−1+1=5+1⟹4y=6.
- عكس القسمة: اضرب طرفي المعادلة في 4: 4y×4=6×4⟹y=24.
- التحقق: 424−1=6−1=5 (الحل صحيح).
- حل المعادلة −3a+6=−9:
- العمليات المؤثرة على a: الضرب في -3 ثم الجمع مع 6.
- عكس الجمع: اطرح 6 من طرفي المعادلة: −3a+6−6=−9−6⟹−3a=−15.
- عكس الضرب: اقسم طرفي المعادلة على -3: −3−3a=−3−15⟹a=5.
- التحقق: −3(5)+6=−15+6=−9 (الحل صحيح).
أهمية المعادلات ذات الخطوتين وتطبيقاتها المتنوعة
تكتسب المعادلات ذات الخطوتين أهمية كبيرة في بناء الفهم الجبري وتطبيق المفاهيم الرياضية في سياقات مختلفة:
- بناء الفهم الجبري الأساسي: تُعد المعادلات ذات الخطوتين جسرًا هامًا بين فهم العمليات الحسابية وحل المعادلات الأكثر تعقيدًا. تعلم كيفية عزل المتغير باستخدام العمليات العكسية هو مهارة أساسية في الجبر.
- تطوير مهارات حل المشكلات: تتطلب حل المعادلات ذات الخطوتين تحليل المشكلة وتحديد الخطوات اللازمة للوصول إلى الحل، مما يعزز مهارات التفكير النقدي وحل المشكلات.
- ربط المفاهيم الرياضية بالمسائل الكلامية: يمكن ترجمة العديد من المسائل الكلامية البسيطة إلى معادلات ذات خطوتين، مما يساعد الطلاب على فهم كيفية تطبيق المفاهيم الجبرية في سياقات واقعية.
- التأسيس لمفاهيم أكثر تعقيدًا: فهم كيفية حل المعادلات ذات الخطوتين يمهد الطريق لفهم وحل المعادلات متعددة الخطوات، والمتباينات، وأنظمة المعادلات، والدوال.
- التطبيقات في العلوم: تظهر المعادلات ذات الخطوتين بشكل مبسط في بعض القوانين والمفاهيم العلمية الأساسية، مما يساعد في فهم العلاقات بين المتغيرات الفيزيائية والكيميائية. على سبيل المثال، بعض العلاقات الخطية البسيطة يمكن تمثيلها وحلها باستخدام معادلات ذات خطوتين.
أمثلة على مسائل كلامية يمكن حلها باستخدام معادلات ذات الخطوتين:
- “إذا أضفنا 5 إلى ضعف عدد ما، كان الناتج 17. ما هو العدد؟” (المعادلة: 2x+5=17)
- “بعد خصم 3 دولارات من سعر قميص، أصبح سعره 12 دولارًا. ما هو السعر الأصلي للقميص؟” (المعادلة: x−3=12) – هذه معادلة ذات خطوة واحدة، ولكن يمكن توسيعها لتصبح ذات خطوتين.
- “إذا قمنا بتقسيم عدد ما على 3 ثم طرحنا 2، كان الناتج 4. ما هو العدد؟” (المعادلة: 3x−2=4)
الخاتمة
تُمثل المعادلات ذات الخطوتين نقطة محورية في تعلم الجبر، حيث تقدم تحديًا بسيطًا ولكنه بالغ الأهمية لتطبيق فهم العمليات الحسابية واستخدام العمليات العكسية لعزل المتغير. إن إتقان حل هذه المعادلات يمنح الطلاب أساسًا متينًا للانطلاق نحو مفاهيم جبرية أكثر تعقيدًا ويعزز قدرتهم على ترجمة وحل المشكلات الكلامية في الرياضيات والعلوم. تظل المعادلات ذات الخطوتين أداة قيمة في بناء الفهم الجبري وتطوير مهارات التفكير الرياضي الأساسية.


